需要率、不等率、負荷率とその活用（電験過去問付） | 音声付き電気技術解説講座

法規の計算問題はほとんどが施設管理の項目で出題されている。主なものとして水力発電所の流水の利用と送受電電力量、変電所や需要設備におけるコンデンサーによる力率改善と各種の損失軽減、変圧器の損失と全日効率、送電線の風圧加重・弛み、配電線路の電圧降下・短絡電流、需要率・不等率・負荷率の活用などがある。今回は需要率・不等率・負荷率の活用についてポイントを解説する。

関連講座（変圧器・リアクトル）「変圧器の電圧変動率と損失及び効率計算」

Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.

　需要設備は、例えば電灯は夜間、電動機などは昼間を主として使用され、暖房と冷房は季節によって需要状態が異なる。また、1需要家においても、その需要設備が常にすべて運転されるわけでなく、その一部は休止状態にあり、さらに同一種類の需要家でもその使用時刻が一致するわけではない。また、需要設備が常時全負荷で使用されることは少ない。

　こうしたことから、供給設備容量は需要設備容量の100％でなく何割かの負荷で供給できる設備とすればよいことになる。

　このような需要設備と供給設備の関係を表す係数に需要率、不等率、負荷率がある。

← 解説講座HPのトップに戻る ← 需要設備のトップに戻る ↑ ページトップに戻る

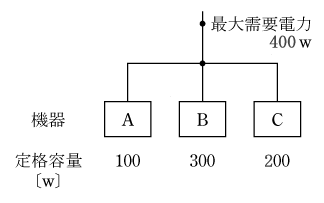
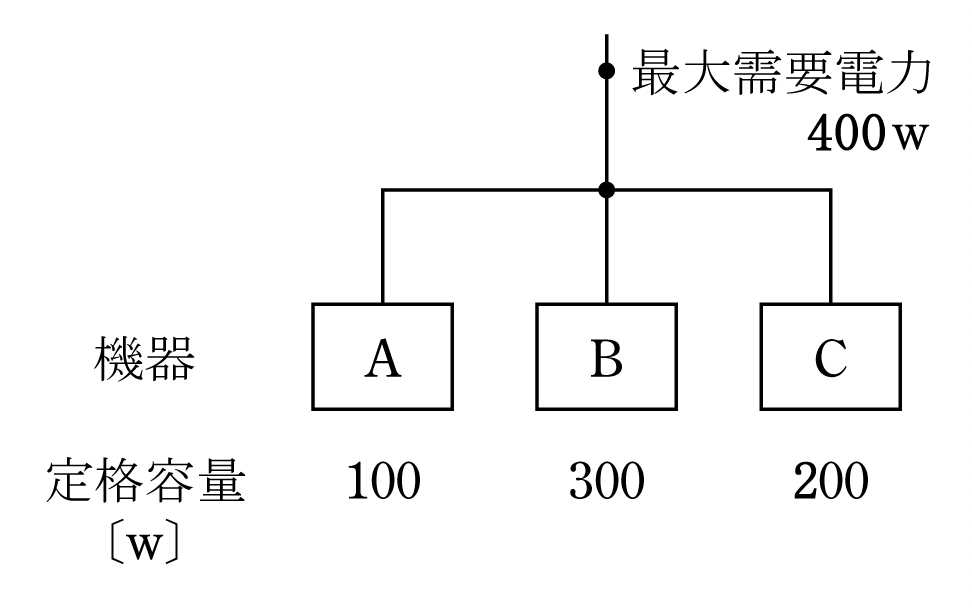
　需要家に設置された電気機器の設備容量の合計は各機器に明示されているので直ぐに分かるが、実際に使われる最大需要電力(一般には1時間の平均電力)は前章で述べたように、電気機器を1日中使っているわけではなく、すべてが全負荷で働いていることもないので、設備容量の合計=全設備容量より小さい。これらの関係を表す係数を需要率といい、( 1 )式のように表される。

〔%〕　　　　　　　　　　　　　　　　　(1)

〔%〕　　　　　　　　　　　　　　　　　( 1 )

　例えば、それぞれの機器の定格容量と実際の最大需要電力の関係を第1図とすると、

〔%〕

　このように、需要率は100%以下である。

■第1図　需要率■

　ここで、需要率は100%以下であることと定義並びに第1図が重要である。

← 解説講座HPのトップに戻る ← 需要設備のトップに戻る ↑ ページトップに戻る

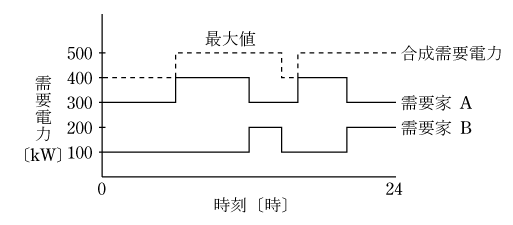
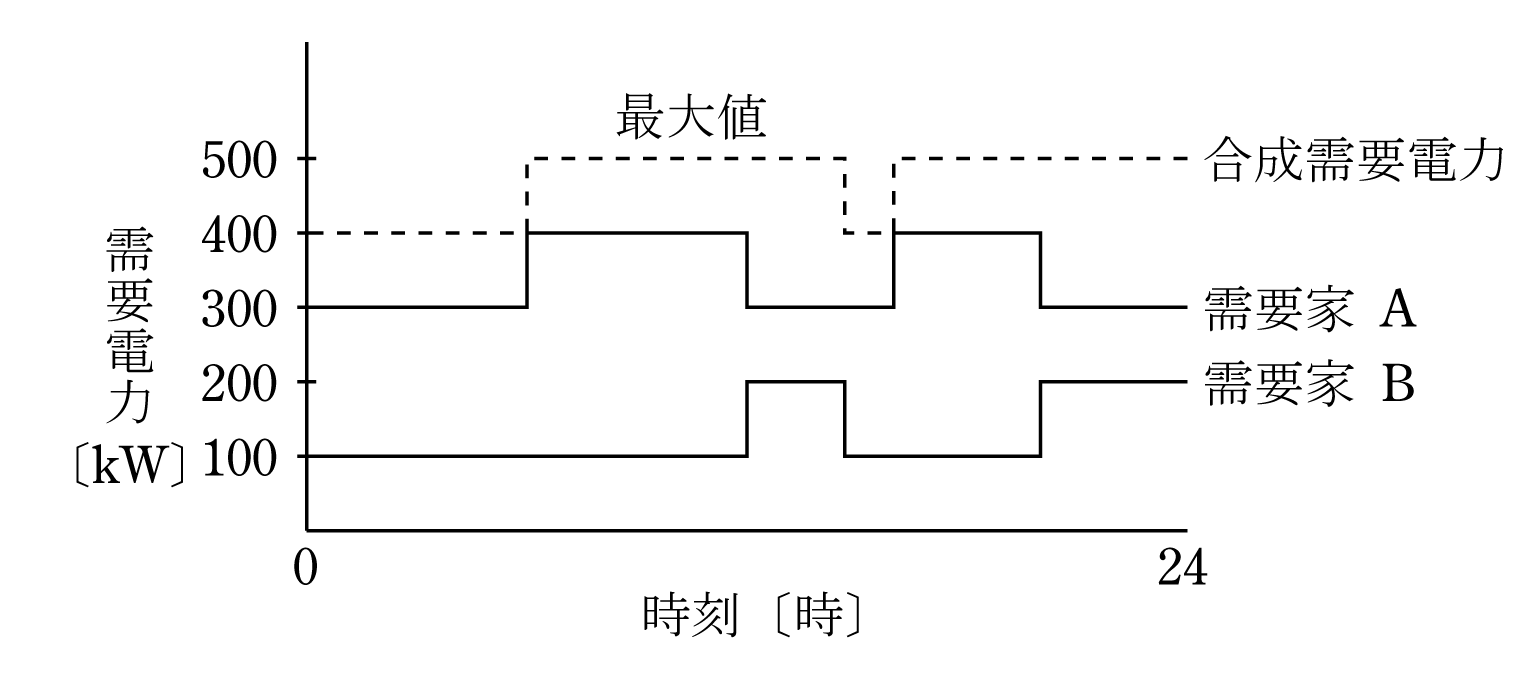
　各需要家の1日の電力の使われ方は例えばA、B需要家の場合第2図に示すように最大需要電力の発生時刻は必ずしも一致しないので、両者を合成した合成需要電力を点線でします。このときの合成最大需要電力と個々の需要家の最大需要電力の関係を不等率といい( 2 )式のように表される。

　　　　　　　　(2)

　第2図から不等率を求めると

　合成最大需要電力は点線から500kW、A、B需要家の最大需要電力の合計は200+400=600 kWから

　このように、不等率は必ず1以上になる。

■第2図　不等率■

　ここで、不等率は1以上であることと定義並びに第2図のように個々の需要家の最大需要電力図を活用して合成最大需要電力を点線のように描いて求めることが重要である。

← 解説講座HPのトップに戻る ← 需要設備のトップに戻る ↑ ページトップに戻る

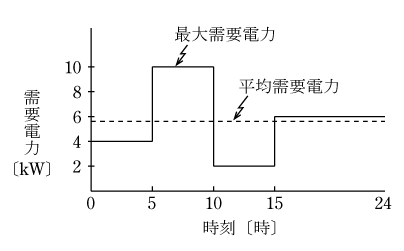
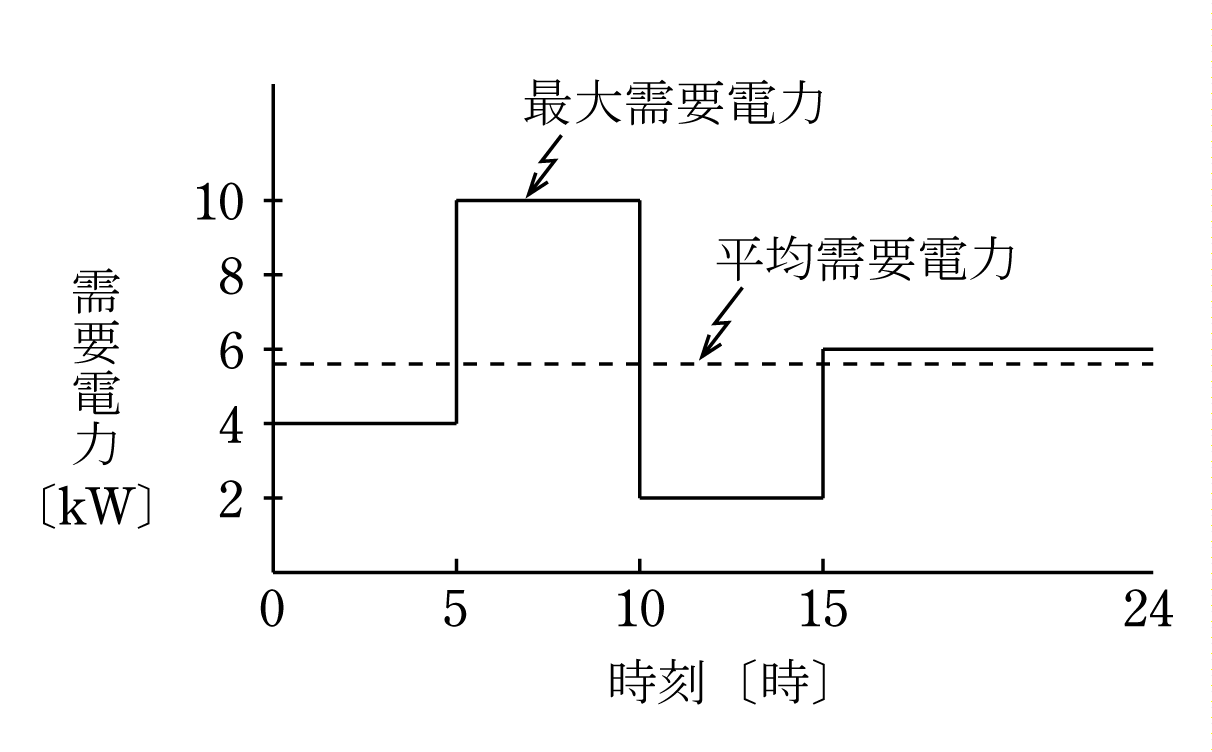
　電力の使用状態は第3図の負荷曲線に示すように1日24時間の時刻で変化し、さらに季節によっても変化する。ある期間中の需要電力の平均値=平均需要電力とその期間中の最大需要電力との比をパーセントで表したものを負荷率といい( 3 )式で表される。

〔%〕　　　　　　　　　　　　　　　　　 (3)

〔%〕　　　　　　　　　　　　　　　　　(3)

　ここで第3図の日負荷曲線から負荷率を求めると、最大需要電力は10kW、平均需要電力は図を活用して

　1日の使用電力量kWh=電力×時間の合計を求め、1日24時間で割り算して求めることができますので、

　　　　　　平均需要電力= 〔kW〕

〔%〕

　このように負荷率は100%以下になります。

■第3図　負荷率■

　ここで、負荷率は100%以下であることと定義並びに第3図を活用して平均需要電力を求めることが重要である。

　次に、負荷率には総合負荷率があります。これは複数の需要家を対象とするもので(4)式のように表されます。

〔%〕　　　　　　　　　　　　　　　　　(4)

← 解説講座HPのトップに戻る ← 需要設備のトップに戻る ↑ ページトップに戻る

　需要率・不等率・負荷率・総合負荷率の定義( 1 )( 2 )( 3 )( 4 )式を使って最大需要電力、合成最大需要電力、平均需要電力の算出に活用することが重要です。

　・最大需要電力=全設備容量×需要率

　・合成最大需要電力=個々の需要家の最大需要電力の合計／不等率

　=（個々の需要家の全設備容量×需要率）の合計／不等率

　・平均需要電力=最大需要電力×負荷率

　=全設備容量×需要率×負荷率

　・総合負荷率=合成平均需要電力／合成最大需要電力

← 解説講座HPのトップに戻る ← 需要設備のトップに戻る ↑ ページトップに戻る

　過去において、需要率・不等率・負荷率に関する問題は文章問題、計算問題を含めてほぼ毎年度出題されている。今回は主な問題のポイントを解説する。

( 1 )総合負荷率についての文章問題

　次の文章は、複数の需要家を総合した場合の負荷率（以下、「総合負荷率」という。）と各需要家の需要率及び需要家間の不等率との関係についての記述である。これらの記述のうち、正しいのは次のうちどれか。

　　ただし、この期間中の各需要家の需要率はすべて等しいものと仮定する。

　（1）総合負荷率は、需要率に反比例し、不等率に比例する。

　（2）総合負荷率は、需要率には関係なく、不等率に比例する。

　（3）総合負荷率は、需要率及び不等率の両方に比例する。

　（4）総合負荷率は、需要率に比例し、不等率に反比例する。

　（5）総合負荷率は、需要率に比例し、不等率には関係しない。

　解答

　総合負荷率は5章を利用し問題では各需要家の需要率はすべて等しいとしているので

　総合負荷率=合成平均需要電力／合成最大需要電力

　　　　　　　　　=合成平均需要電力／( 個々の需要家の全設備容量×需要率の合計／不等率 )

　　　　　　　　　=合成平均需要電力×不等率／個々の需要家の全設備容量×需要率の合計

　　　　　　　　　=合成平均需要電力×不等率／個々の需要家の全設備容量の合計×需要率

　から総合負荷率は不等率に比例し需要率に反比例する。

　回答　( 1 )

( 2 )負荷曲線を用いた不等率、総合負荷率の計算問題

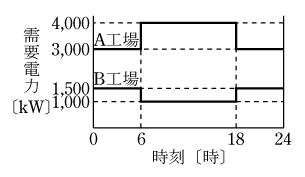
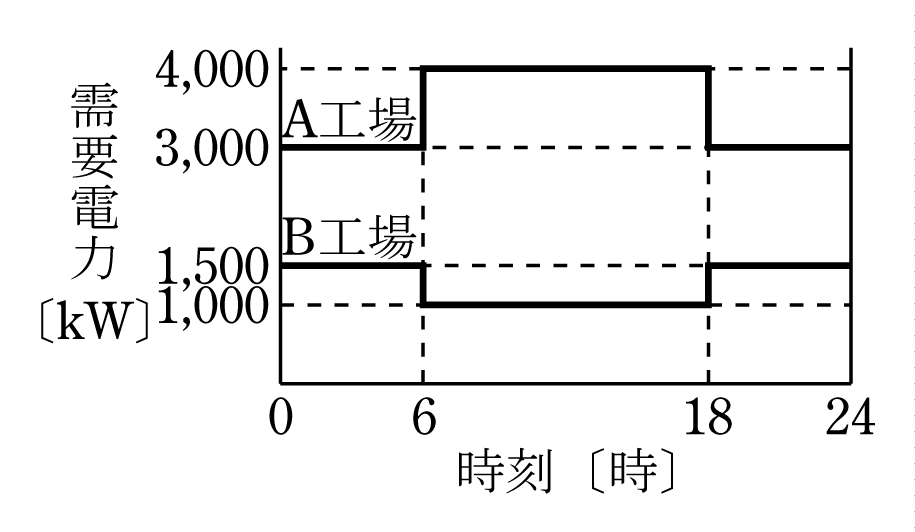
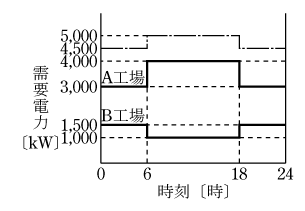
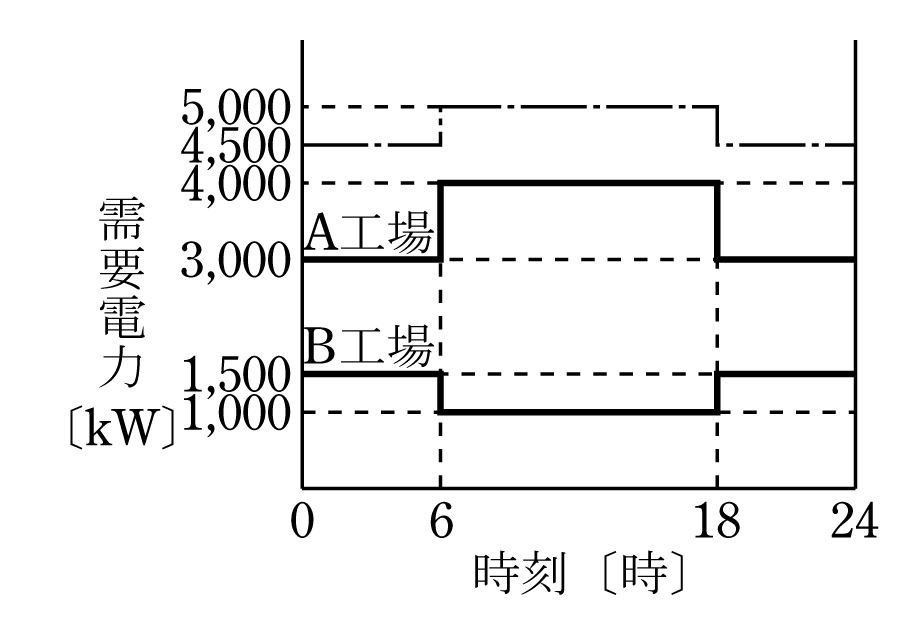
　図のような負荷曲線を持つA工場及びB工場があるとき，次の（a）及び（b）に答えよ．

■第4図　問題図1■

　（a）A及びB両工場の需要電力の不等率の値として，正しいのは次のうちどれか．　　

　　　（1）0．9　（2）1．0　（3）1．1　（4）1．2　（5）1．3

　（b）A及びB両工場の総合負荷率[％]の値として，正しいのは次のうちどれか・

　　　（1）91　（2）92　　（3）93　（4）94　（5）95

　( a )の解答

　第4図を活用して両工場の負荷曲線の和を計算すると第5図のような合成負荷曲線となる。図から、

　合成最大電力=5000kW、各工場の最大需要電力の和=4000+1500=5500

　不等率は( 2 )式から

　回答　( 3 )

　( b )の解答

　第5図から両工場の合成負荷の平均需要電力を計算すると

　合成最大電力=5000kW

　から(4 )式に導入すると総合負荷率は

〔%〕

　回答 ( 5 )

■第5図　回答図1■

　ポイントは問題図を活用して第5図を作成して計算することである。

( 3 )需要率、不等率、負荷率と総合負荷率の総合計算問題

　AとBの二つの変電所を持つ工場がある。ある期間において，A変電所は負荷設備の定格容量の合計が500〔kW〕，需要率90〔％〕，負荷率60〔％〕であり，B変電所は負荷設備の定格容量の合計が300〔kW〕，需要率80〔％〕，負荷率50〔％〕であった。二つの変電所間の不等率が1．3であるとき，次の（a）及び（b）に答えよ。

　（a）工場の合成最大需要電力〔kW〕の値として，最も近いのは次のうちどれか。

　　　（1）346　　　（2）450　　　（3）531　　（4）615　　（5）690

　（b）工場を総合したこの期間の負荷率〔％〕の値として，最も近いのは次のうちどれか。

　　　（1）55．0　　（2）56．5　　（3）63．4　　（4）73．5　　（5）86．7

　( a )の解答

　以下のようにA、B変電所に分けて下部に需要率、負荷率、不等率を表示してそれぞれを計算します。

	A変電所	B変電所
設備容量〔kW〕	500	300
需要率〔%〕	90	80
最大需要電力〔kW〕	500×0.9=450	300×0.8=240
負荷率〔%〕	60	50
平均需要電力〔kW〕	450×0.6=270	240×0.5=120
不等率	1.3
合成最大需要電力〔kW〕