変圧器の2次端子に,定格力率において定格電流となるような負荷を接続し,その端子電圧が2次定格電圧V2nになるように1次電圧を与え,1次電圧を一定に保ったまま無負荷にしたときの2次電圧をV20とすると,電圧変動率εは(1)式で表されます。
![]() 〔%〕 (1)
〔%〕 (1)
この定義に基づいて,変圧器の等価回路から電圧変動率を求めます。変圧器の等価回路は一般に第1図に示すL形等価回路で表されます。

この等価回路は1次電圧を基準とし,励磁電流によるインピーダンス降下を無視しています。ここに,a は巻数比,V1, V2は1次および2次電圧,I1, I2は1次および2次電流,Y0は励磁アドミタンス,r1, r2, x1, x2は1次および2次巻線の抵抗およびリアクタンス,Z2は負荷のインピーダンスです。電圧変動率の計算では,実用的な精度が十分得られることから,さらに簡易的な第2図の等価回路に変換します。
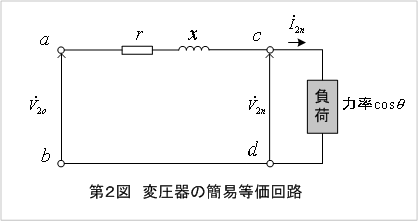
これは,変圧器の励磁アドミタンスを省略し2次側に換算した等価回路であり,端子abの電圧は1次端子電圧V1を2次側に換算したもので(2)式に示すV20となります。
![]() (2)
(2)
ここに,r,xはそれぞれ2次側に換算した抵抗およびリアクタンスで、
![]() ,
,![]() (3)
(3)
となります。また,I2nは2次定格電流とします。
そこで,これらの関係をベクトル図に表すと第3図となります。ここに、θは負荷の力率角です。
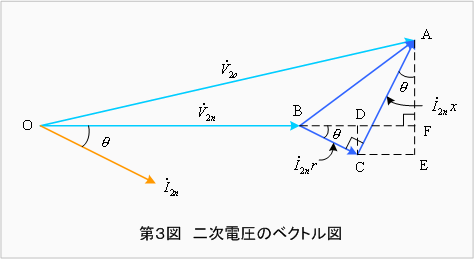
ベクトル図より、
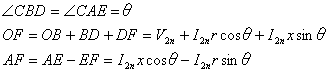 (4)
(4)
したがって、
![]()
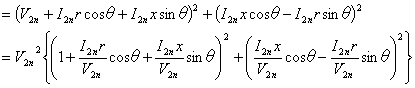 (5)
(5)
ここで,
![]() ,
,![]() (6)
(6)
とおくと,(5)式から、
![]()
![]() (7)
(7)
ここで,(7)式の近似式を得るために(8)式に示す2項定理を利用します。
![]()
![]() (8)
(8)
ここで、
![]() (9)
(9)
とおくと,xは1より小さいので2項定理展開すると,
![]() (10)
(10)
さらに、p',q' の3乗以上の項を省略すると次の近似式が得られます。
![]()
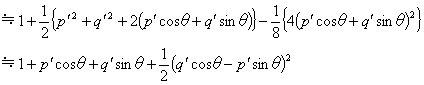 (11)
(11)
したがって,電圧変動率は(1)式より、
![]() (12)
(12)
ここで,p,qを百分率で表した%抵抗降下,%リアクタンス降下とすると,
![]() ,
,
![]() (13)
(13)
とおけるので,電圧変動率は次式のようになります。
![]() 〔%〕 (14)
〔%〕 (14)
(14)式は電圧変動率が大きな変圧器や正確に電圧変動率を計算する場合に使用されます。
電圧変動率が数〔%〕程度の小さい変圧器では,(14)式の第3項が第1項,第2項に比べて小さいことから省略され,次のような簡略式が使用されます。
![]() 〔%〕
(15)
〔%〕
(15)
これは第3図のベクトル図において,OA≒OFと近似して次のように計算したものです。
![]() (16)
(16)
電圧変動率εは(1)式から、
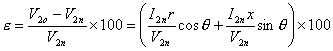
![]()
![]() 〔%〕 (17)
〔%〕 (17)
となります。
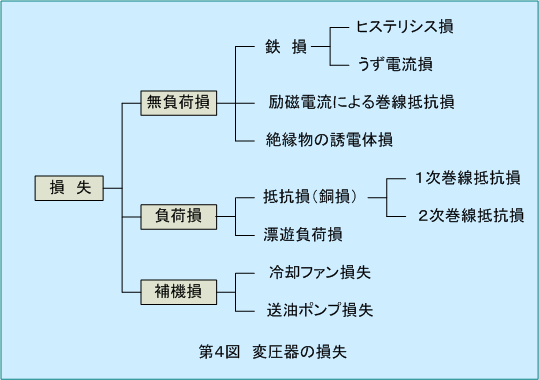
変圧器の損失は詳しく示すと第4図のようになります。変圧器の損失は大別すると,負荷に関係なく発生する無負荷損と負荷電流によって変化する負荷損に分けられます。無負荷損は主として磁束の通路である鉄心に発生する鉄損ですが,その他に励磁電流による巻線の抵抗損や絶縁物の誘電体損が含まれます。
負荷損は主として負荷電流による巻線の抵抗損であり銅損とも呼ばれますが,負荷電流の増加とともに増大する漏れ磁束による表皮効果によって,巻線の実効抵抗が増加することによる抵抗損や巻線以外の金属構造物に発生するうず電流による漂遊負荷損が含まれます。負荷損は基準巻線温度75℃に換算したものが使用されます。その他,変圧器の構造によっては,冷却ファンや送油ポンプなどの補機損があります。一般に鉄損と銅損以外の損失は小さいため,変圧器の損失は鉄損と銅損で表されます。
2−1 鉄損
鉄損Piはヒステリシス損Phとうず電流損Peとの和で表されます。
![]() (18)
(18)
鉄心の磁化曲線はヒステリシス・ループを描くことから,磁束の増加時に蓄積された磁気エネルギーが減少時に完全に放出されず,鉄心中に熱となってエネルギー損失が発生します。この損失をヒステリシス損といいます。
鉄心中で磁束が交番すると,磁束の変化を妨げるような起電力が生じ,これによって鉄心中にうず電流が流れます。このうず電流によって発生する損失をうず電流損といいます。これらの損失は,周波数,1次電圧,磁束密度との間に次の関係があります。
![]() ,
,![]() ,
, ![]() (19)
(19)
![]() ,
,![]() ,
,![]() (20)
(20)
ここに,Ph:ヒステリシス損 Pe:うず電流損
f:周波数
Bm:磁束密度の最大値 V1:1次電圧
(19)式,(20)式からわかるように,鉄損は周波数が一定の場合,1次電圧の2乗に比例します。また一般に,ヒステリシス損はうず電流損に比べて大きいため,1次電圧が一定の場合,鉄損は周波数にほぼ反比例します。
2−2 銅損
銅損は1次および2次巻線抵抗に生ずる抵抗損であり次式で表されます。
![]() (21)
(21)
![]() (22)
(22)
ここに,Pc:全負荷銅損 r1:1次巻線抵抗 r2:2次巻線抵抗
a:巻数比 I1:1次定格電流 I2:2次定格電流
R1:1次換算した巻線抵抗 R2:2次換算した巻線抵抗
(21)式,(22)式より,銅損は負荷電流の2乗に比例します。また,負荷率は負荷電流に比例するため,負荷率αにおける銅損Pcαは,負荷率の2乗に比例して、
![]() (23)
(23)
となります。
2−3 全損失
変圧器の損失は鉄損と銅損以外は非常に小さいため無視され、通常は無負荷損は鉄損を,負荷損は銅損を表し,全損失Wtは無負荷損Piと全負荷損Pcの和として表されます。
![]() (24)
(24)
3−1 効率の計算式
変圧器の損失は一般に小さく,入力と出力の差が少ないので,効率の計算は実際の負荷状態における出力と入力を測定してその比をとる実測効率ではなく,出力と損失を基準として計算する規約効率が用いられます。
![]() 〔%〕 (25)
〔%〕 (25)
![]() 〔%〕 (26)
〔%〕 (26)
定格容量Pn,無負荷損(≒鉄損)Pi,全負荷損(≒銅損)Pcの変圧器が,負荷率α,力率cosθで運転されているときの効率ηは次式で表されます。
![]() 〔%〕
(27)
〔%〕
(27)
ここで,効率が最大となる負荷率を求めてみます。
(27)式の分子,分母をαで割ると、
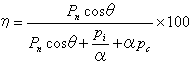 〔%〕 (28)
〔%〕 (28)
ηが最大となるのは,(28)式の分母が最小となるときです。ここで,変動要素となる分母の第2項と第3項に注目すると,2数の積が一定なので,和が最小となるのは2数が等しいときとなります。つまり、
![]() ∴
∴ ![]() (29)
(29)
すなわち,鉄損と銅損が等しいときに最大効率となります。そのときの負荷率は(30)式のようになります。
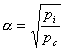 (30)
(30)
最大効率ηm,全負荷効率ηfは(31)式,(32)式で表されます。なお,単に変圧器の効率というときは(33)式に示すように,全負荷で力率1の場合の効率ηaをいいます。
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
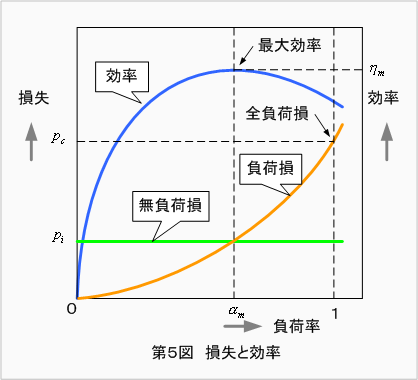
第5図は無負荷損,負荷損,効率の関係をグラフに表したものです。全負荷損と無負荷損の比を損失比γといい,一般の変圧器では2〜6程度のものが多い。
![]() (34)
(34)
したがって,最大効率となる負荷率αmは(30)式により次のような値となります。
![]() (35)
(35)
3−2 全日効率
普通,1日の負荷電力は時間とともに変化します。この1日の出力電力量と入力電力量(出力電力量と損失電力量の和)の比を全日効率ηdといいます。
![]() 〔%〕
(36)
〔%〕
(36)
いま,変圧器の定格容量をPn,無負荷損をPi,負荷損をPcとし,1日をt1,
t2,…, ti,…, t24時に分け,ti
時に対する負荷率をαi,負荷力率をcosθiとすると全日効率は次の式で表されます。
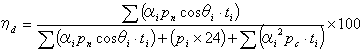 〔%〕 (37)
〔%〕 (37)
1日の損失電力量を少なくするためには、全日効率を大きくするように運転することが必要です。


