~終わり~
■ぜひアンケートにご協力下さい■


[3] 二相短絡一相地絡回路
第12図の回路のようにb相端子とc相端子とが短絡し、a相端子が
![]()
![]() を通して地絡したときの地絡電流及び発電機端の電圧を求めてみよう。
を通して地絡したときの地絡電流及び発電機端の電圧を求めてみよう。
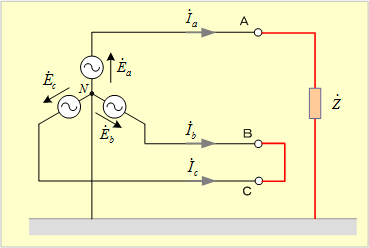

第12図 二相短絡一相地絡回路
*** 1 回路条件 **********************************************
*** 2 対称分変換*********************************************
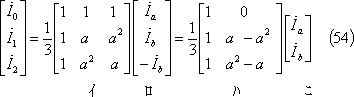
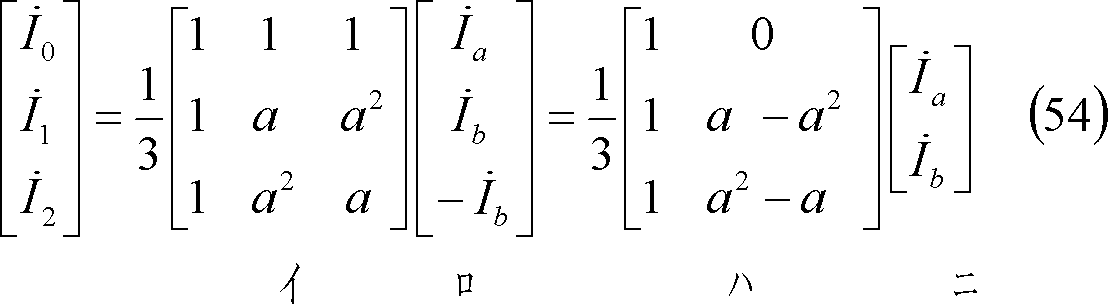
(54)式で、第1行を2倍したものから第2行と第3行を引くと、
![]()
![]() なので、
なので、
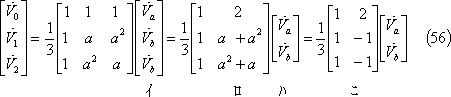
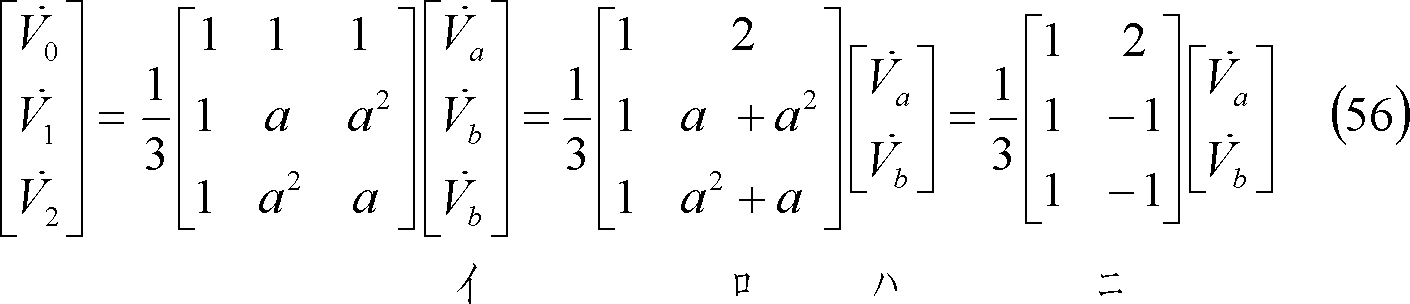
*** 3 対称分回路計算 ***************************************
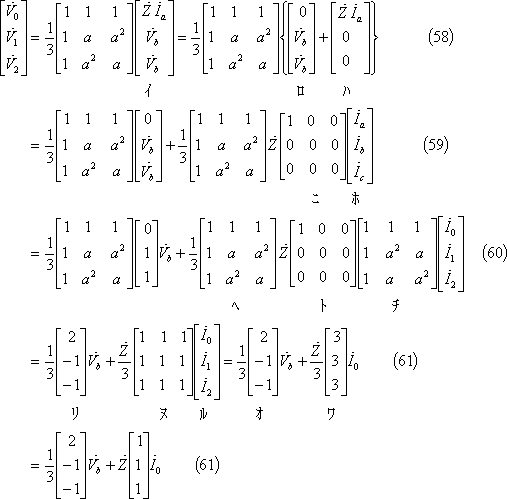
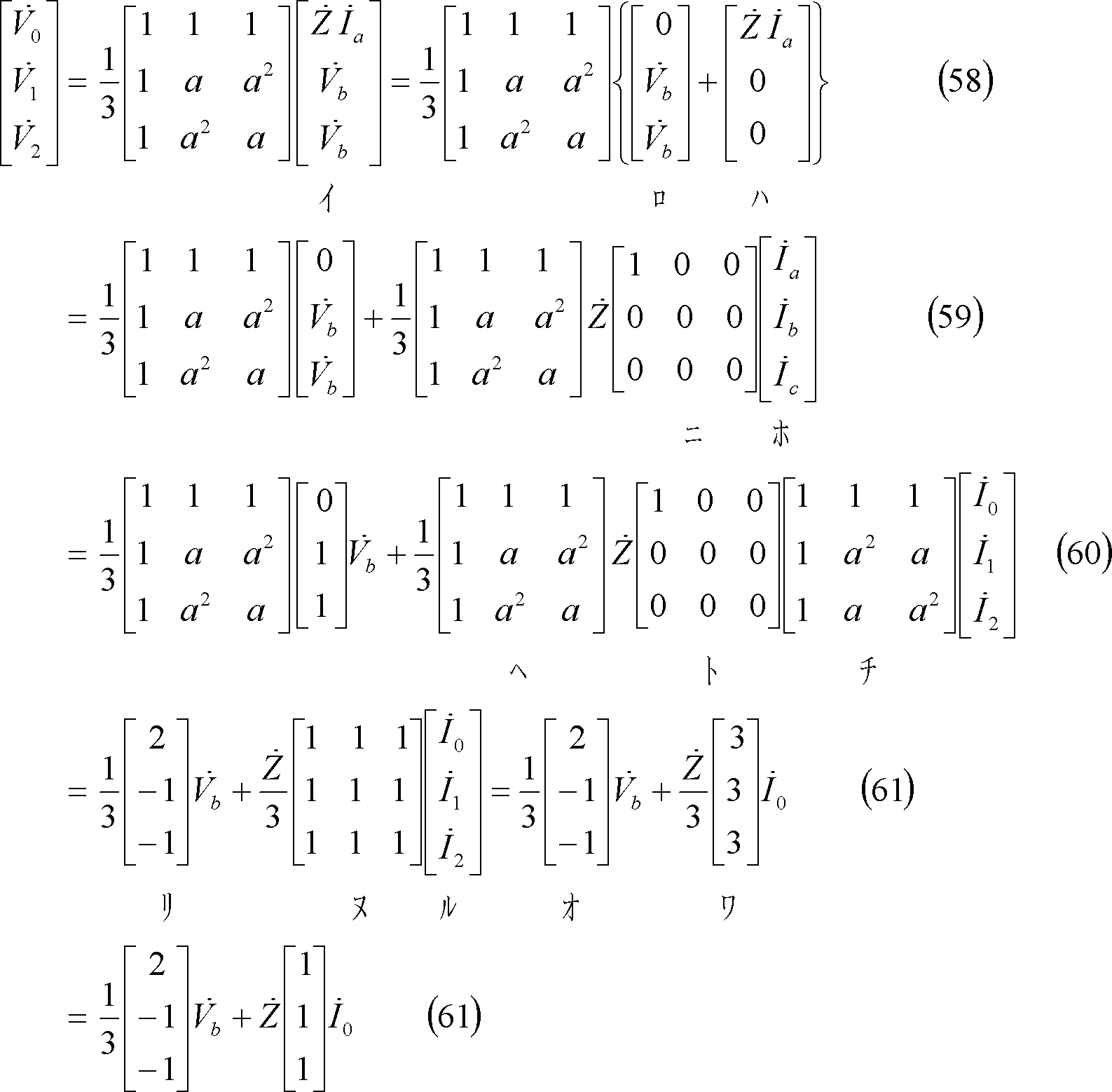
ここで、対称分電圧を整理すると、次のようになる。
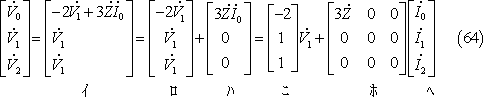
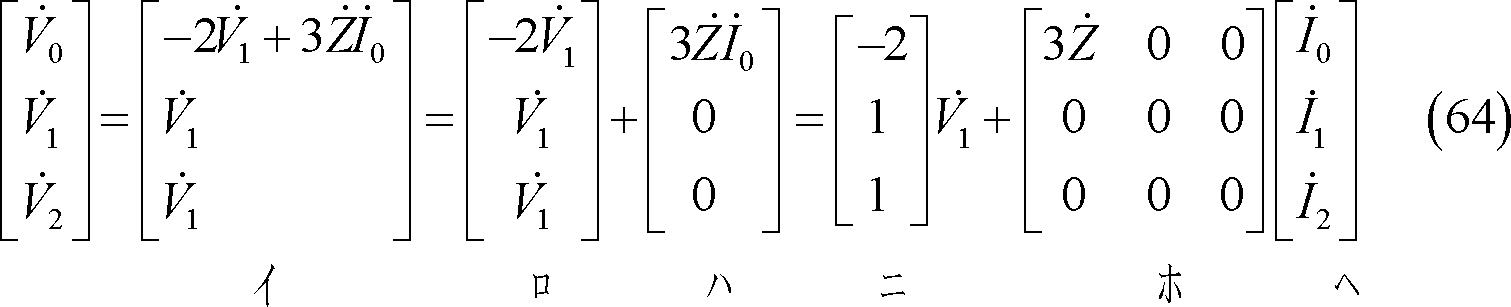
① 式計算の場合
(64)式を発電機の基本式と等値すると(65)式、更に(65)式を整理すると、(67)式となる。
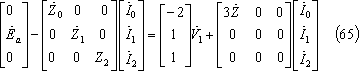
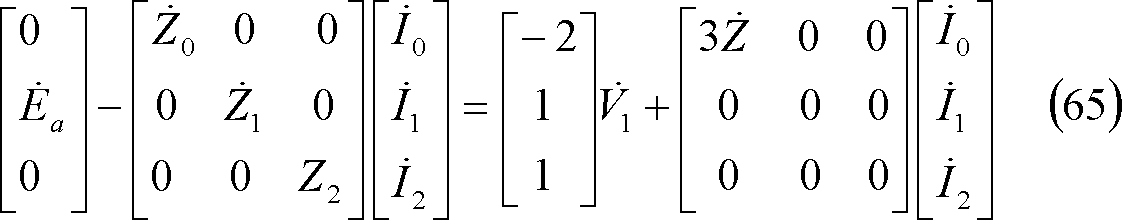
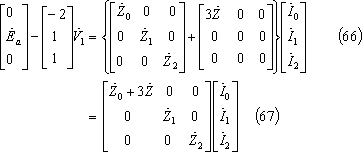
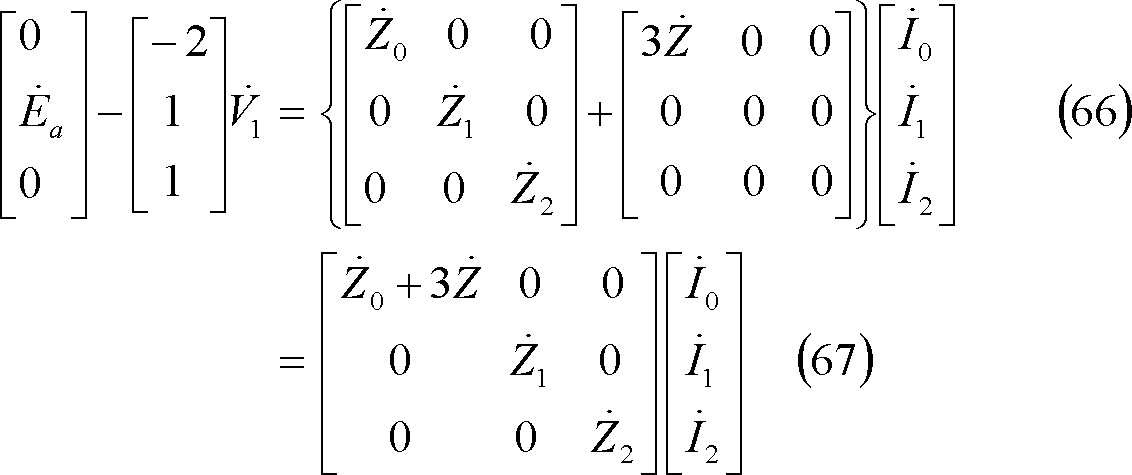
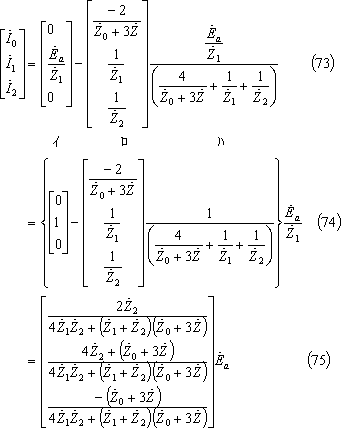
上式を電流の対称分について解けば、(68)式が成立し、同式を前回の(7)~(14)式にならって解けば、(70)式を得る。
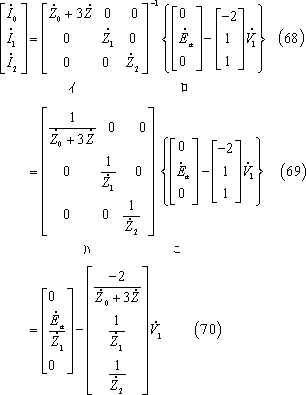
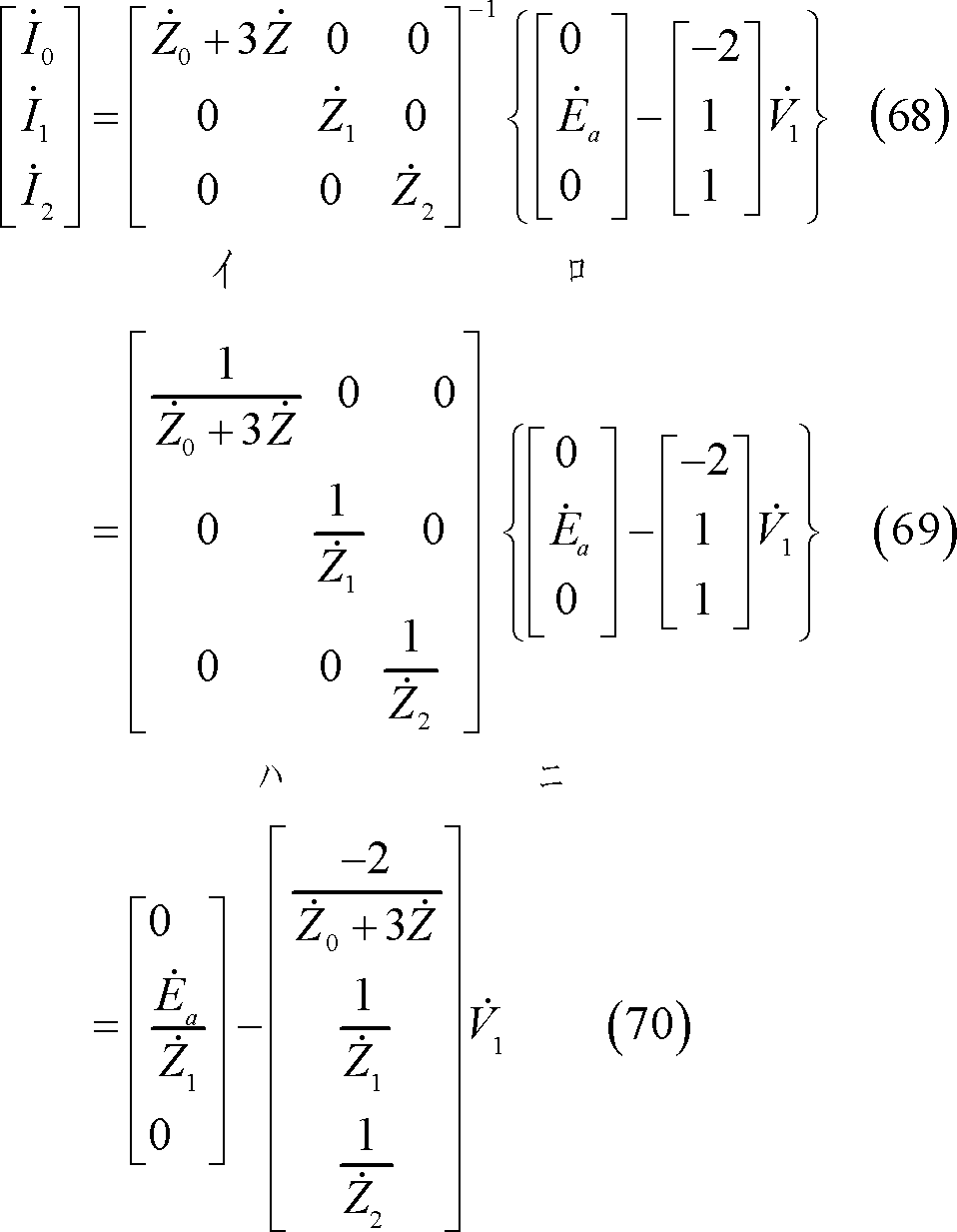
(70)式の第1行を2倍したものと第2行と第3行の和を等値して(71)式、整理して(72)式、
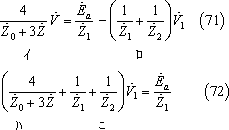
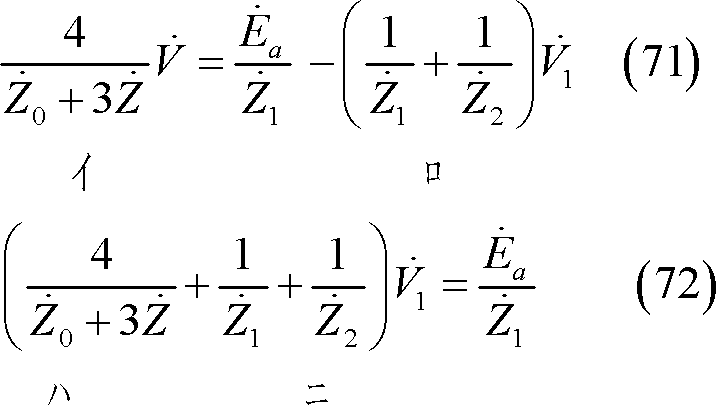
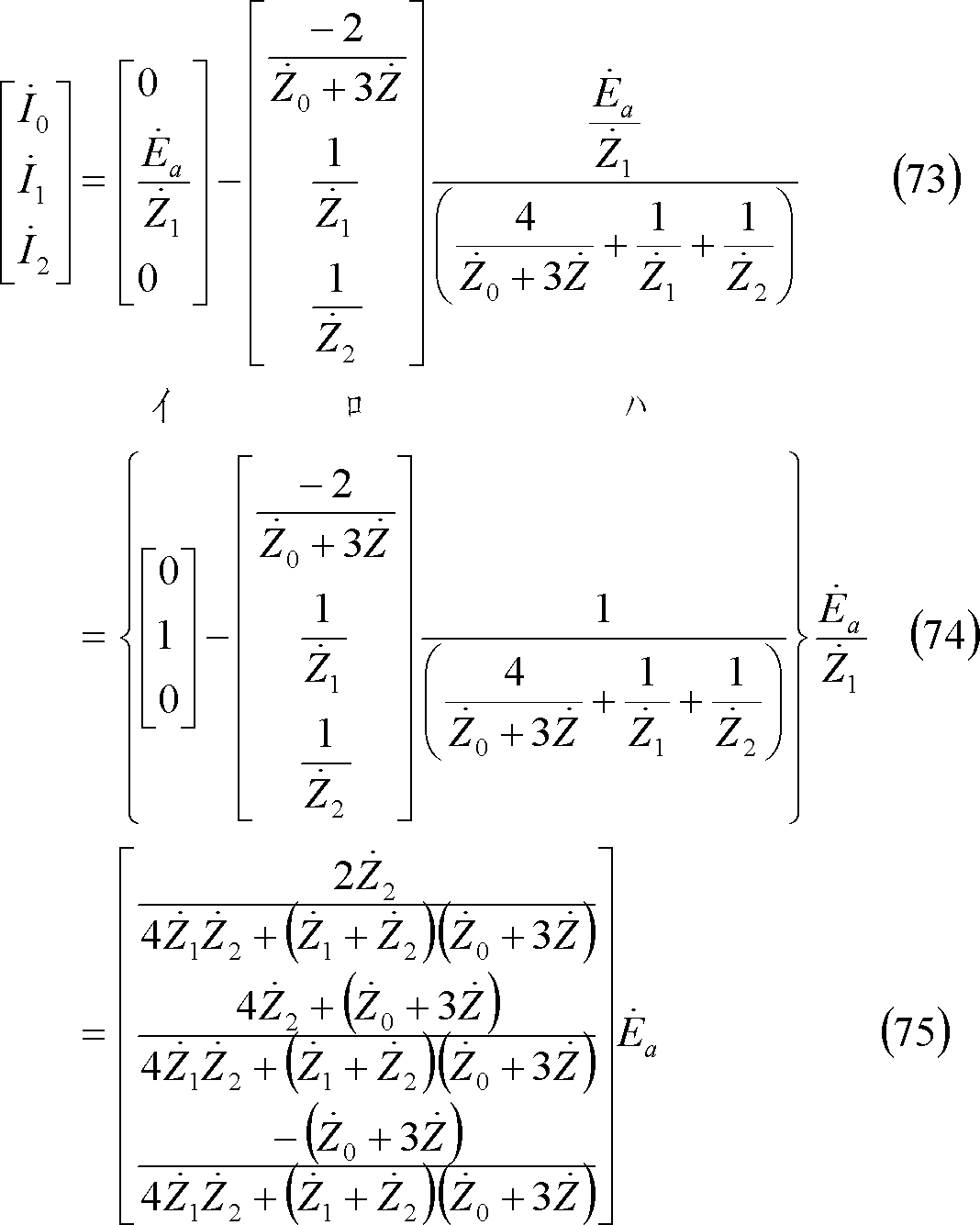
② 図計算の場合 (55),(57)式及び(63)式の関係は、対称分回路が第13図であることを示している。
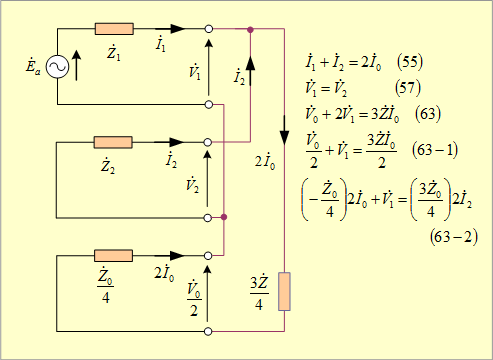

第13図 二相短絡一相地絡回路の対称分回路
したがって、対称分電流は第13図から次のように求めることができる。
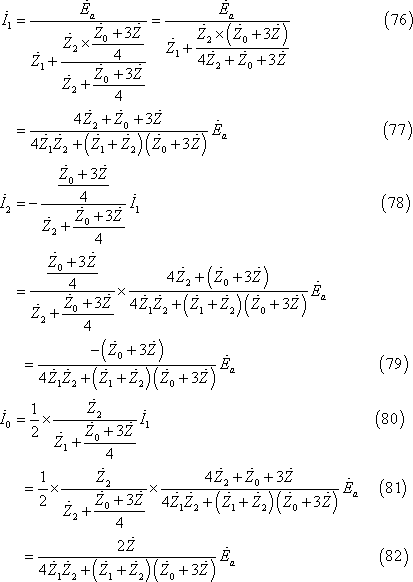
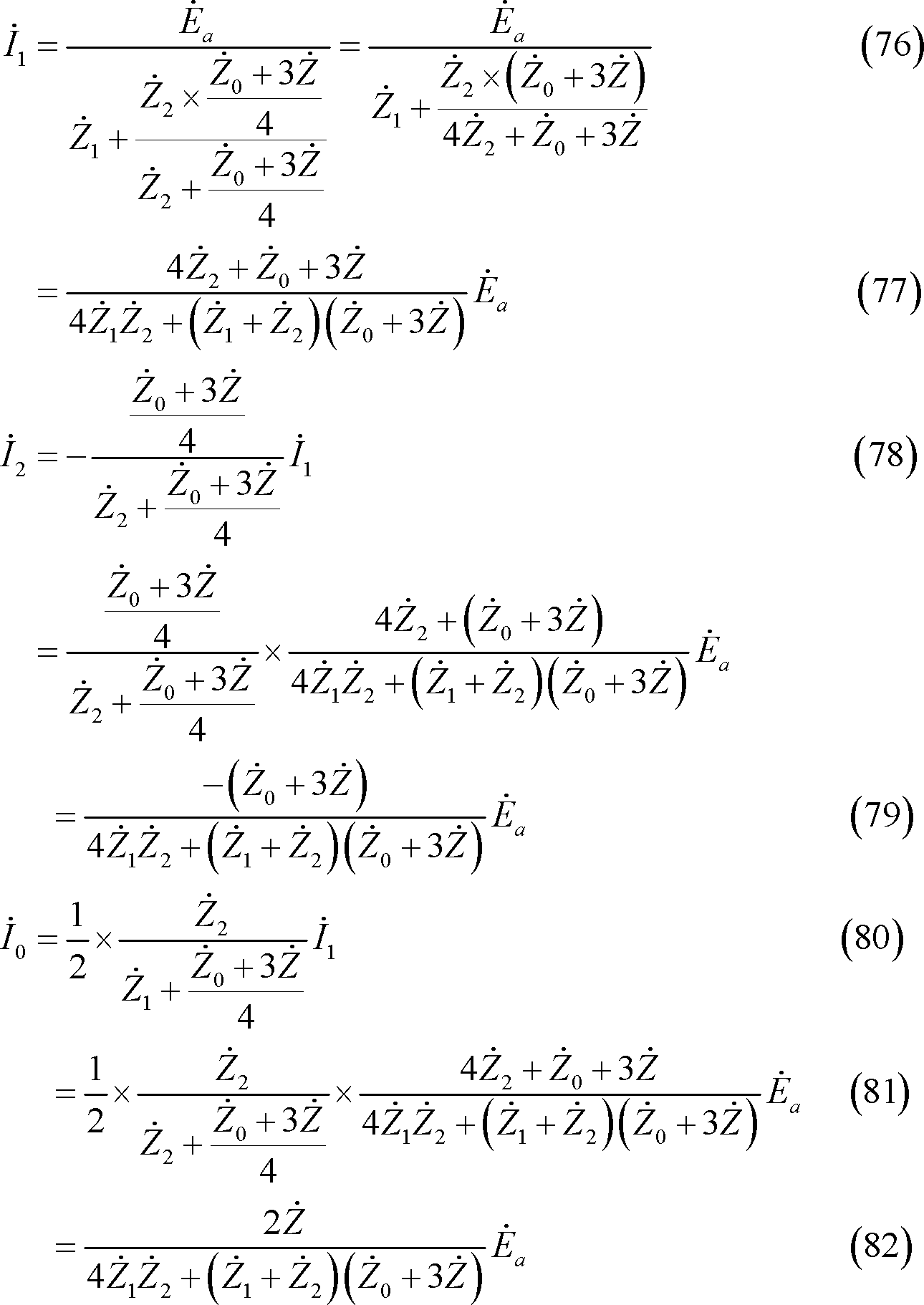
*** 4 逆変換 ***********************************************
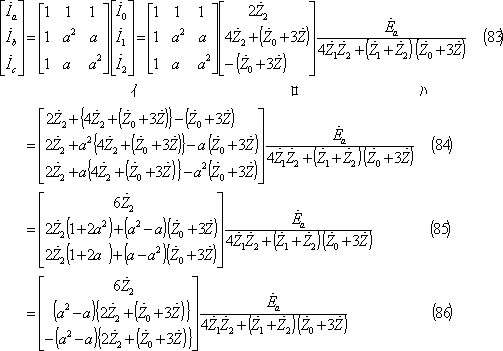
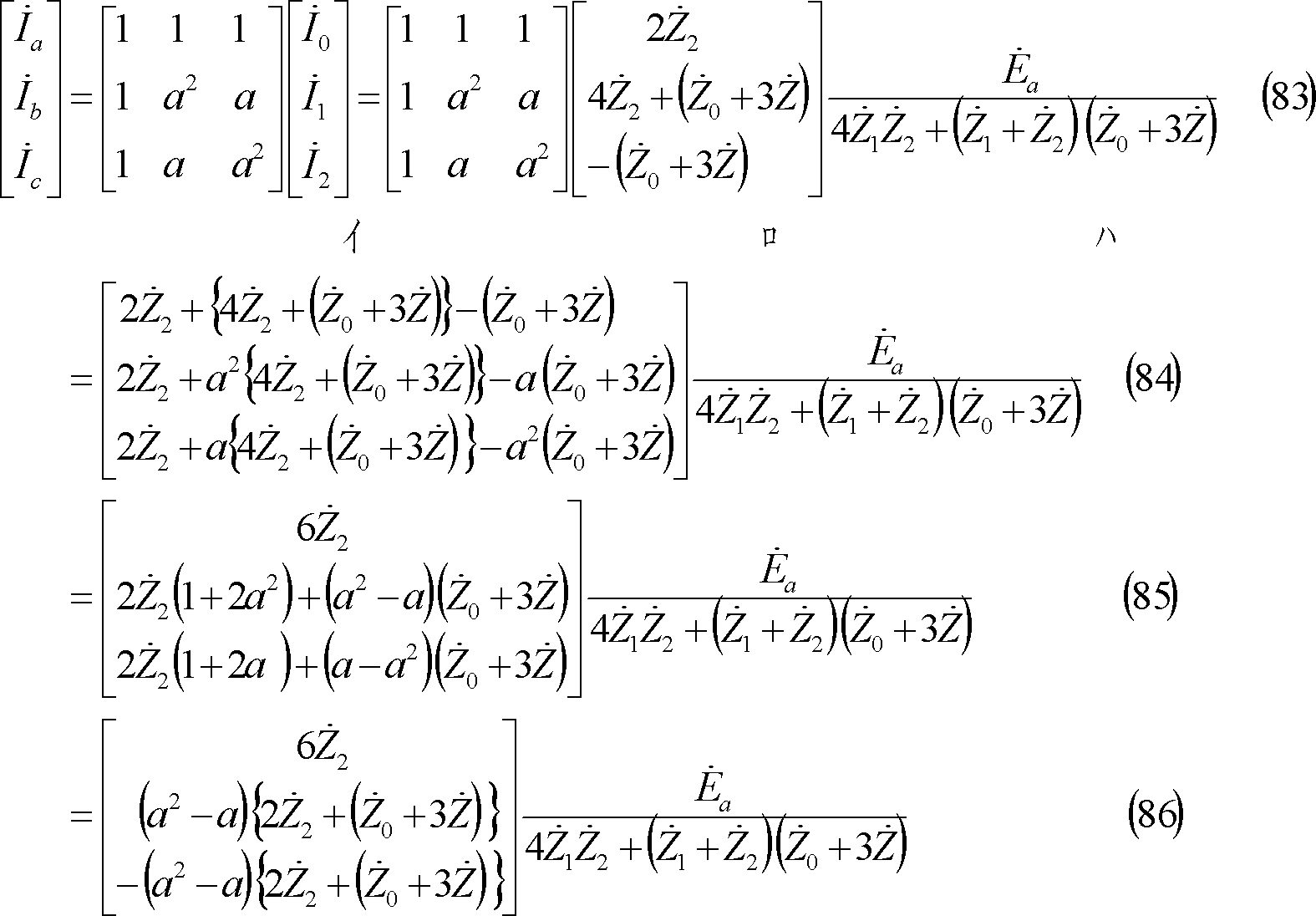
各相電圧は次のようになる。
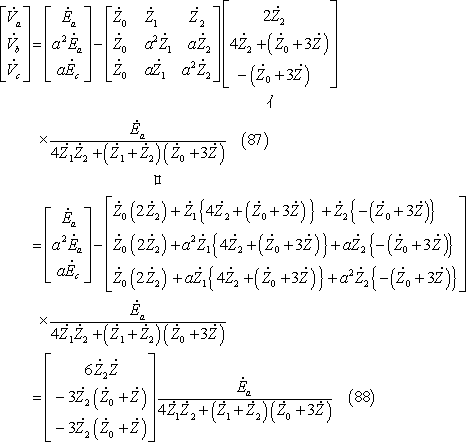
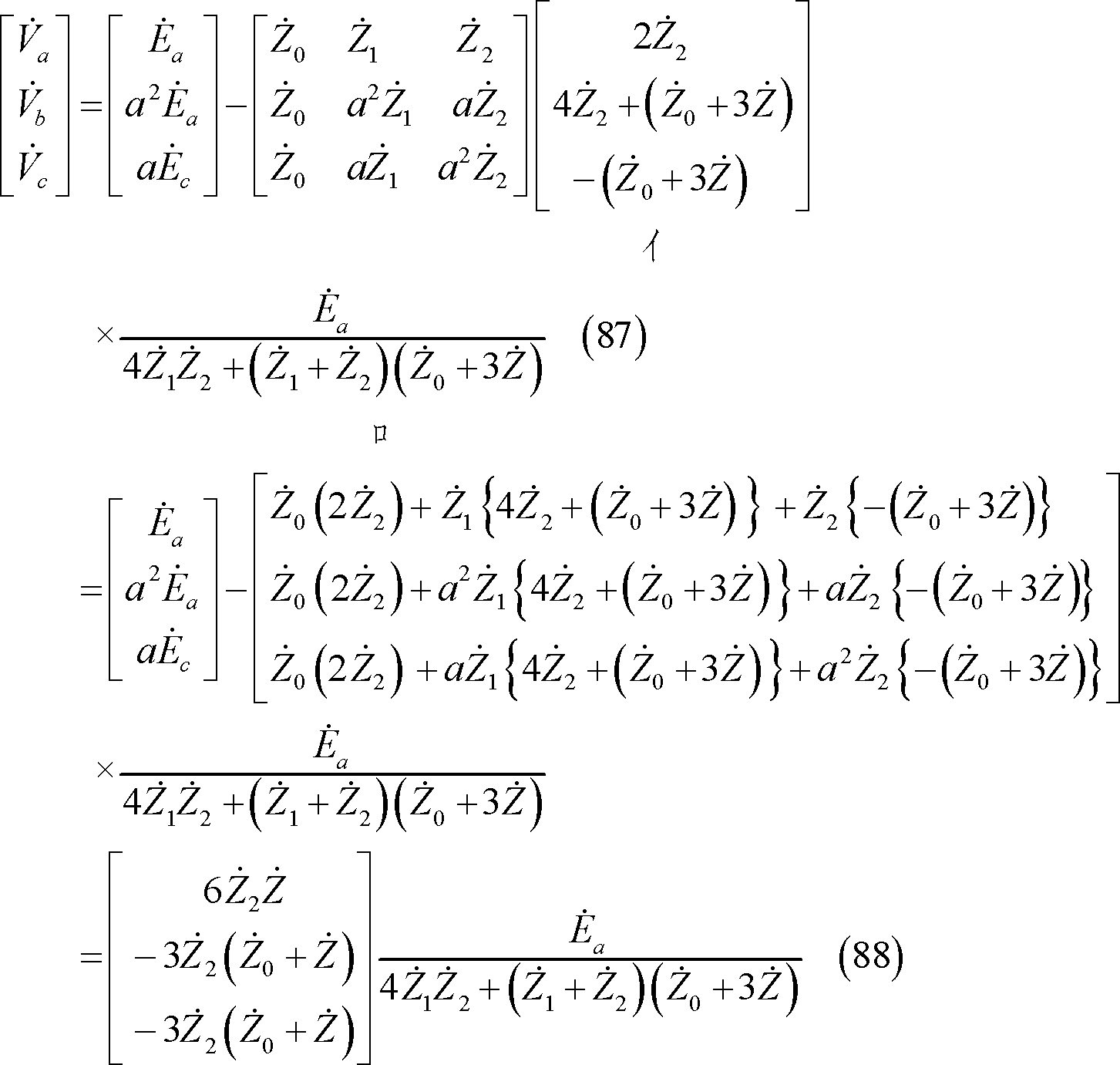
なお、a相電圧は(52)式の回路条件から(86)式で求めた
![]()
![]() を使って次のように求めることもできる。
を使って次のように求めることもできる。
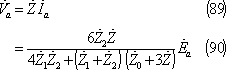
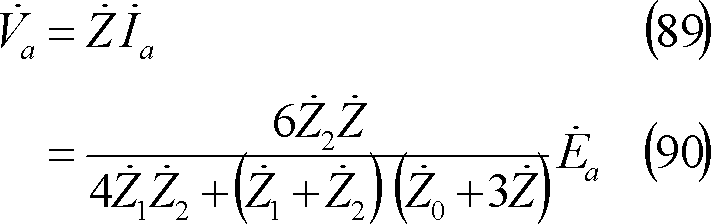
第14図の回路に示すようにb相端子が
![]()
![]() を通して、c相端子が
を通して、c相端子が
![]()
![]() を通して、それぞれ地絡したときの地絡電流及び発電機端の電圧を求めてみよう。
を通して、それぞれ地絡したときの地絡電流及び発電機端の電圧を求めてみよう。
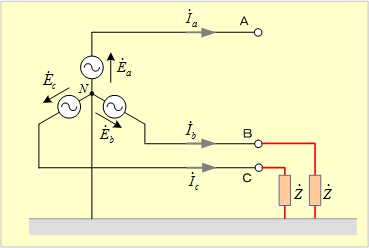

第14図 二相インピーダンス地絡回路
*** 1 回路条件 **********************************************
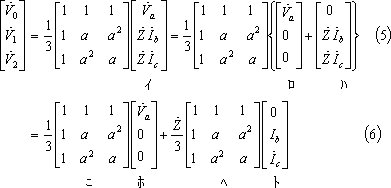
*** 2 対称分変換 ********************************************
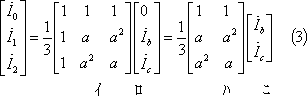
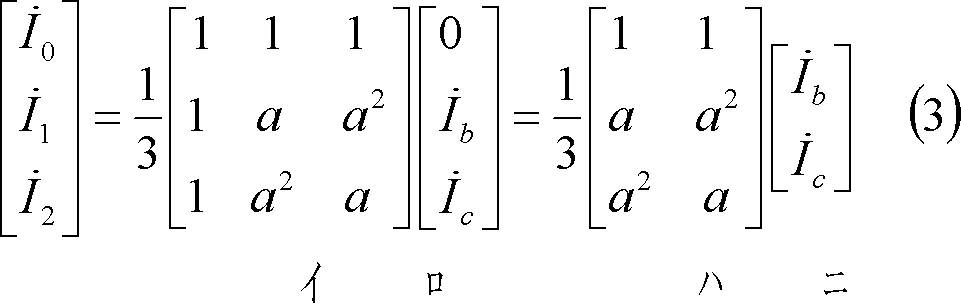
上式のすべての行を加えると、
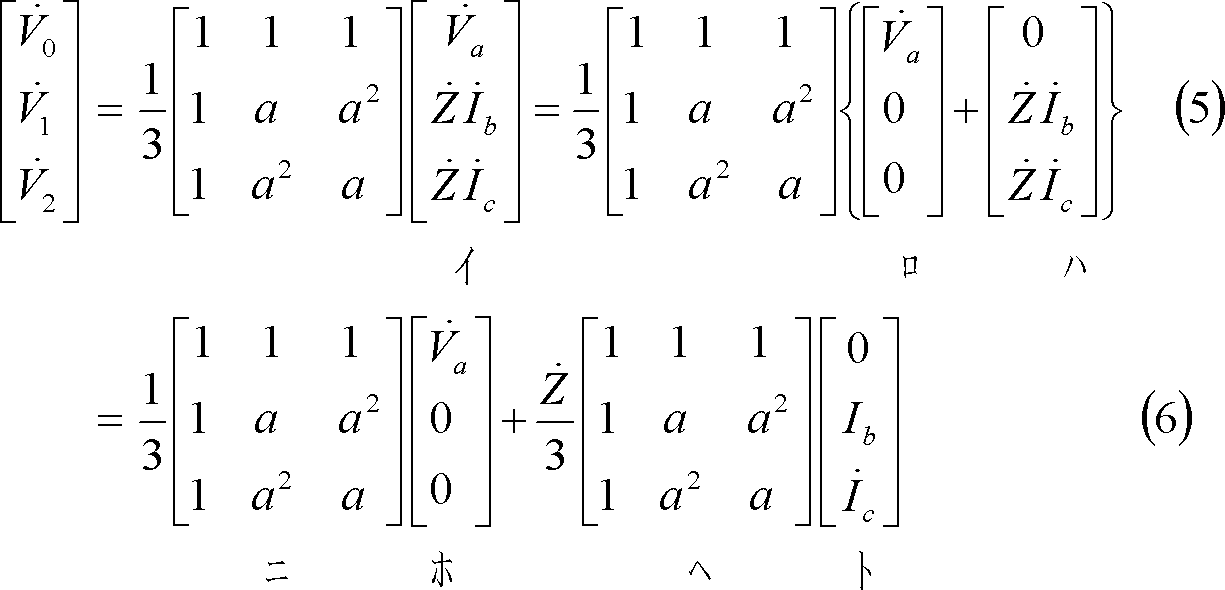
(6)式の右辺第2項は、
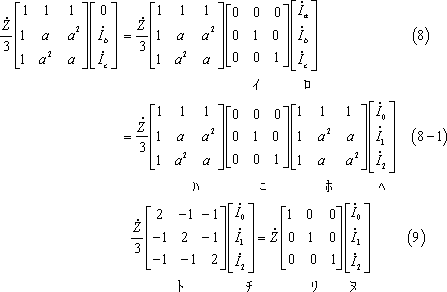
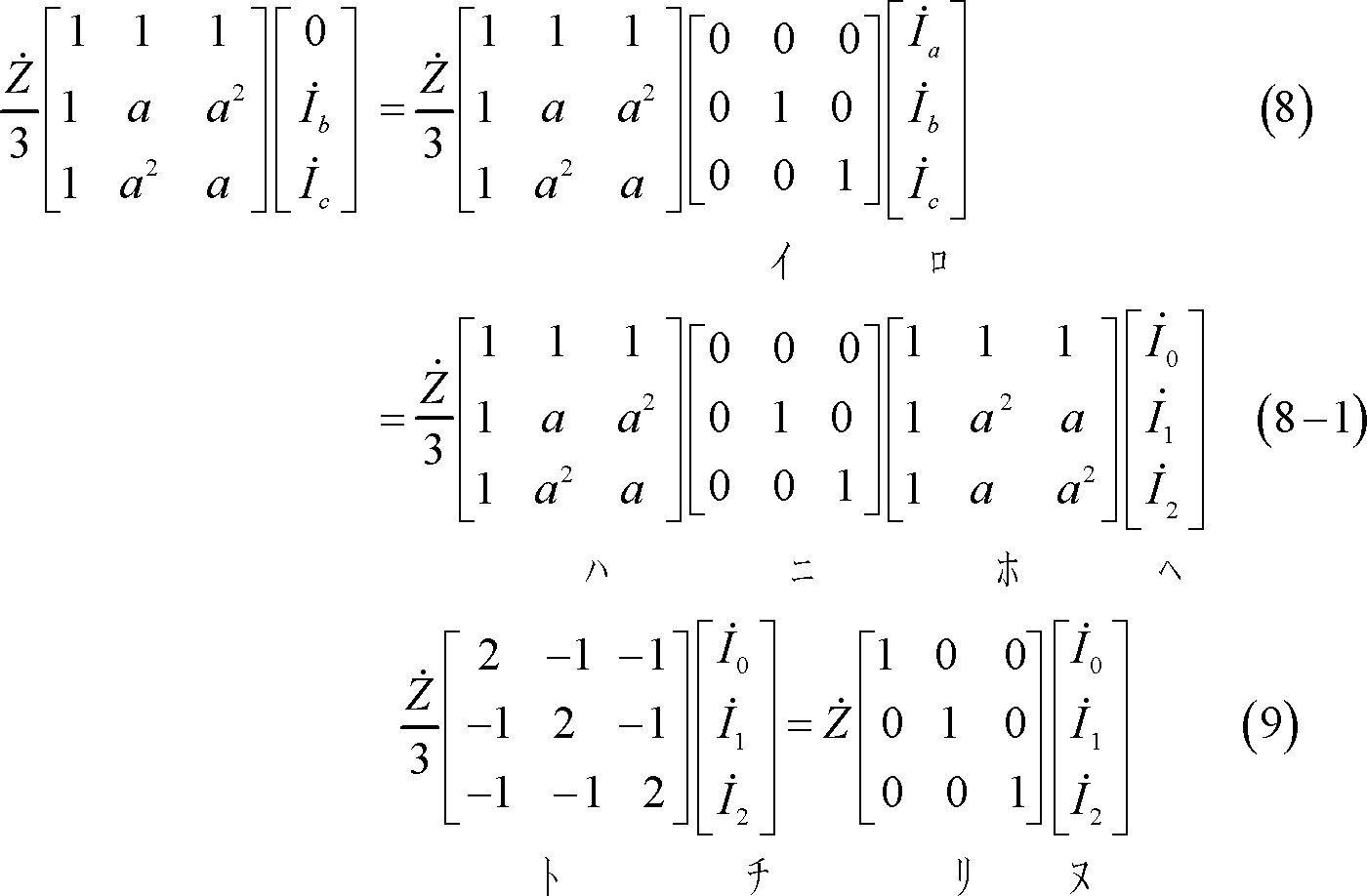
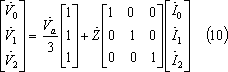
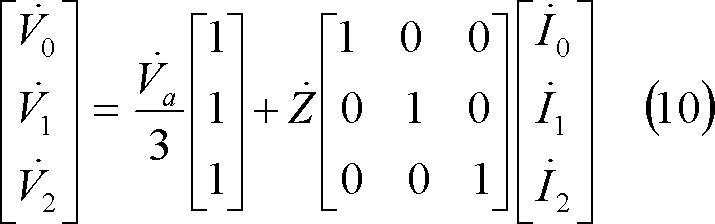
*** 3 対称分回路計算 ***************************************
ここで、上式を発電機の基本式と等値し、整理すると(11)式となる。
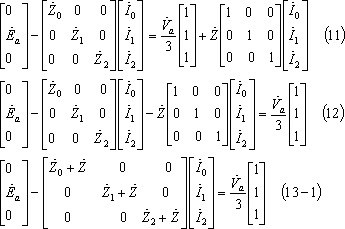
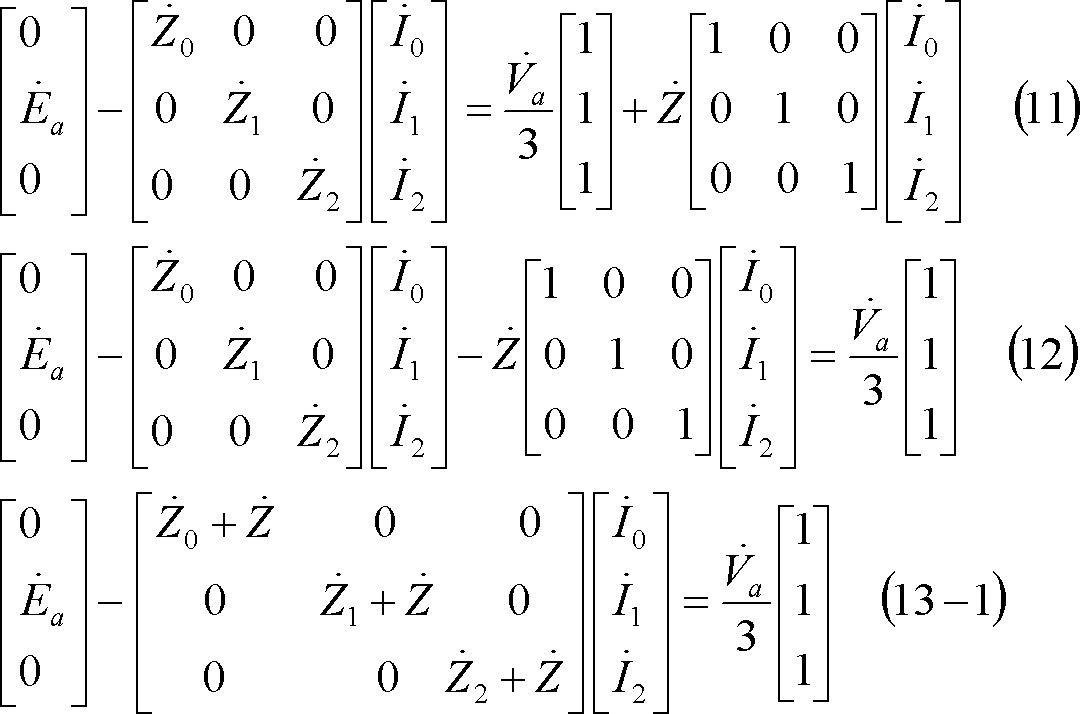
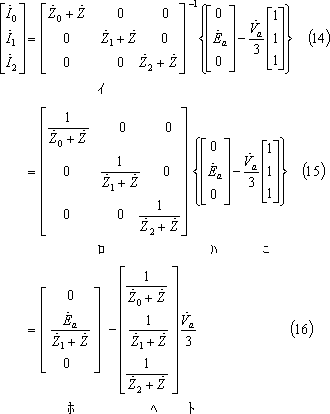
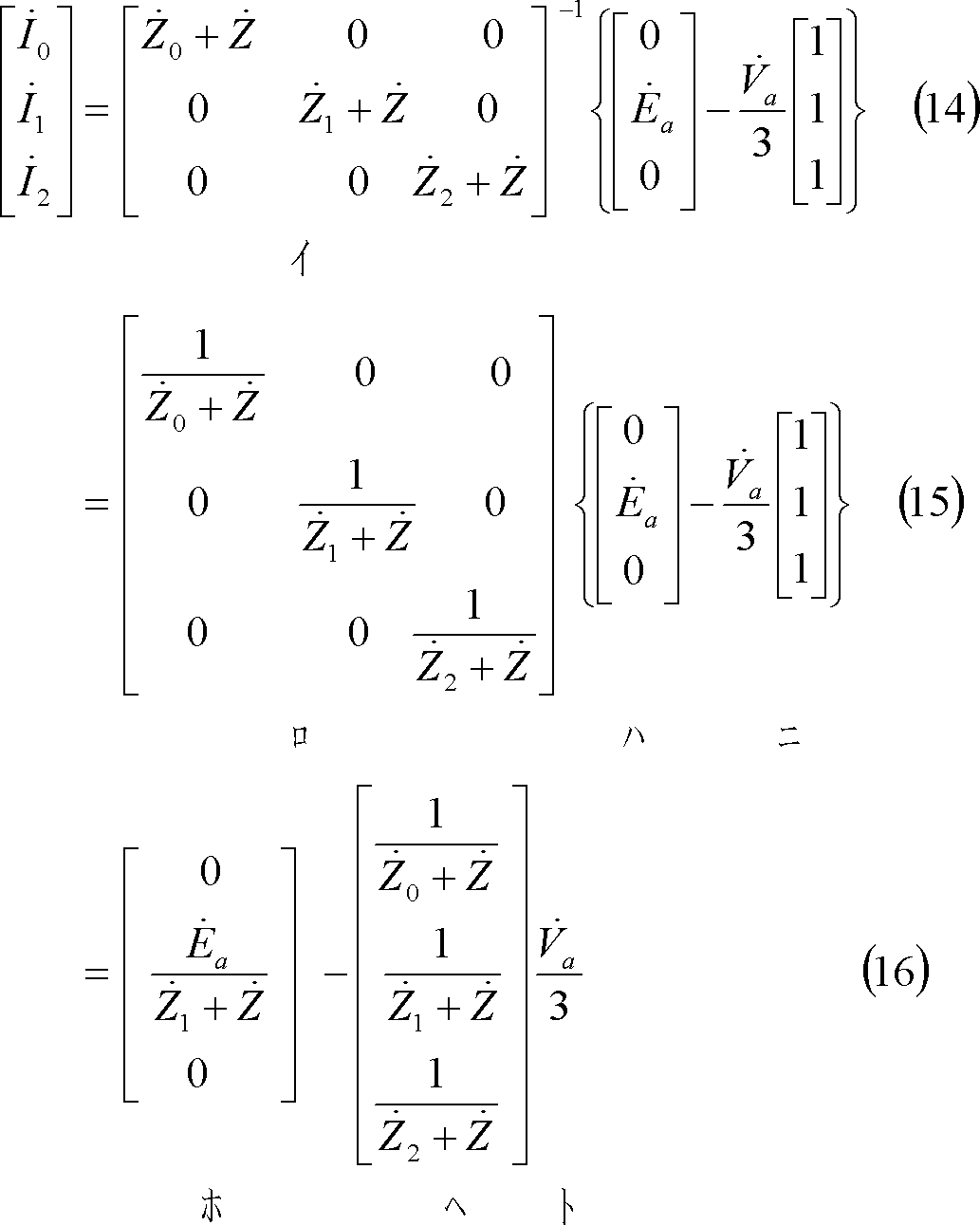
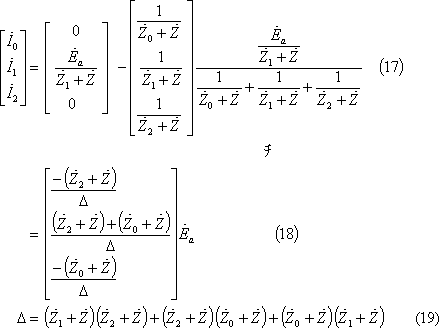
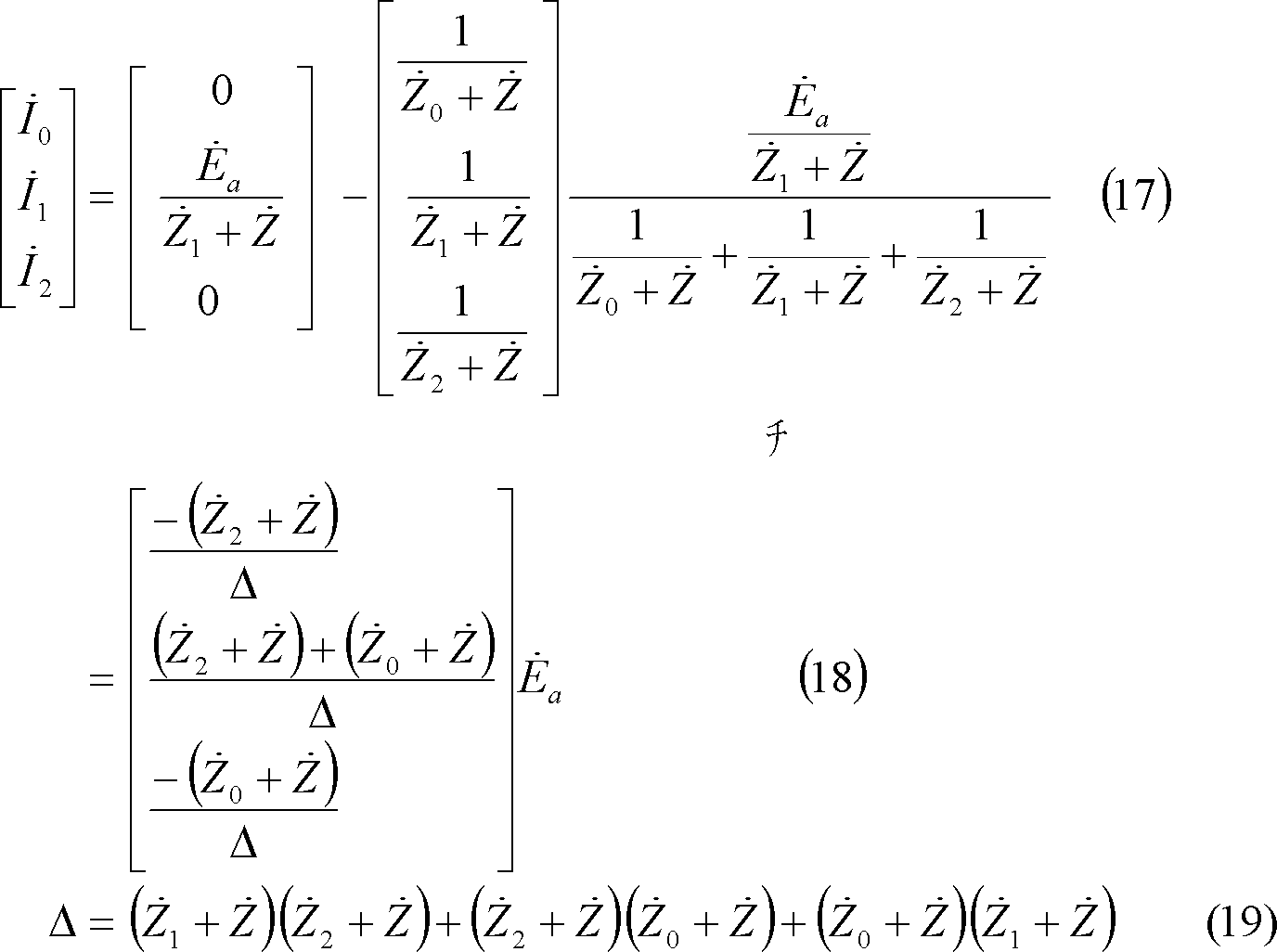
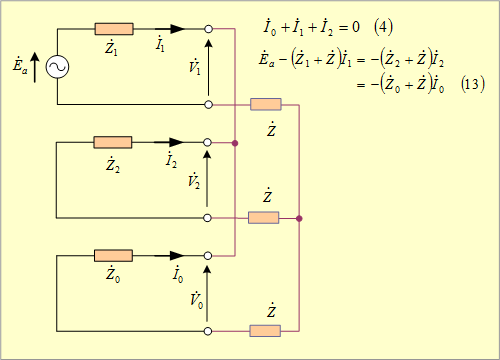

第15図 二相インピーダンス地絡回路の対称分回路
図計算による場合は、(4)式及び(13)式から対称分回路は第15図となる。この結果、電流
![]()
![]() は第15図から次の各式で求められる。
は第15図から次の各式で求められる。
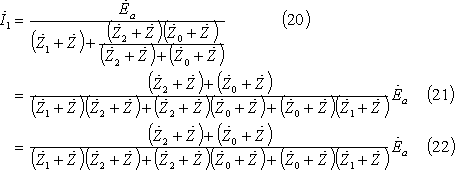
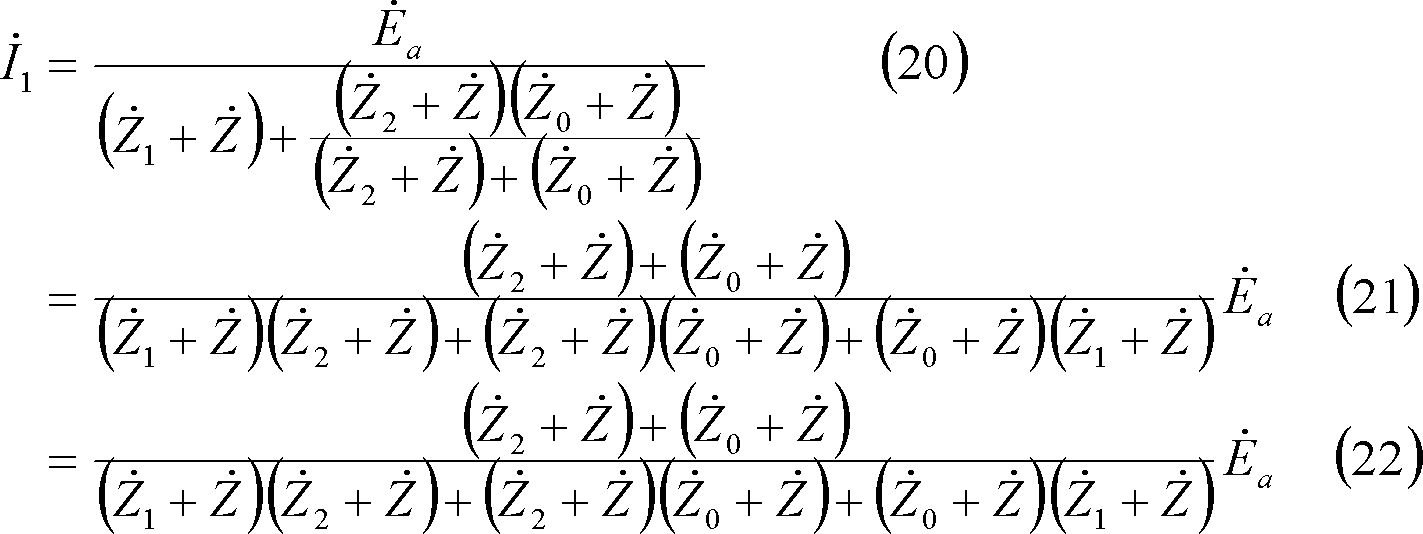
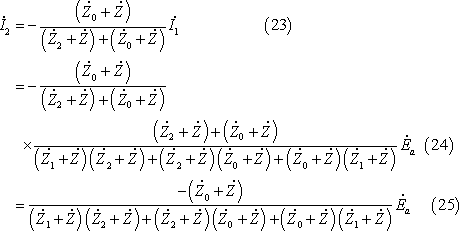
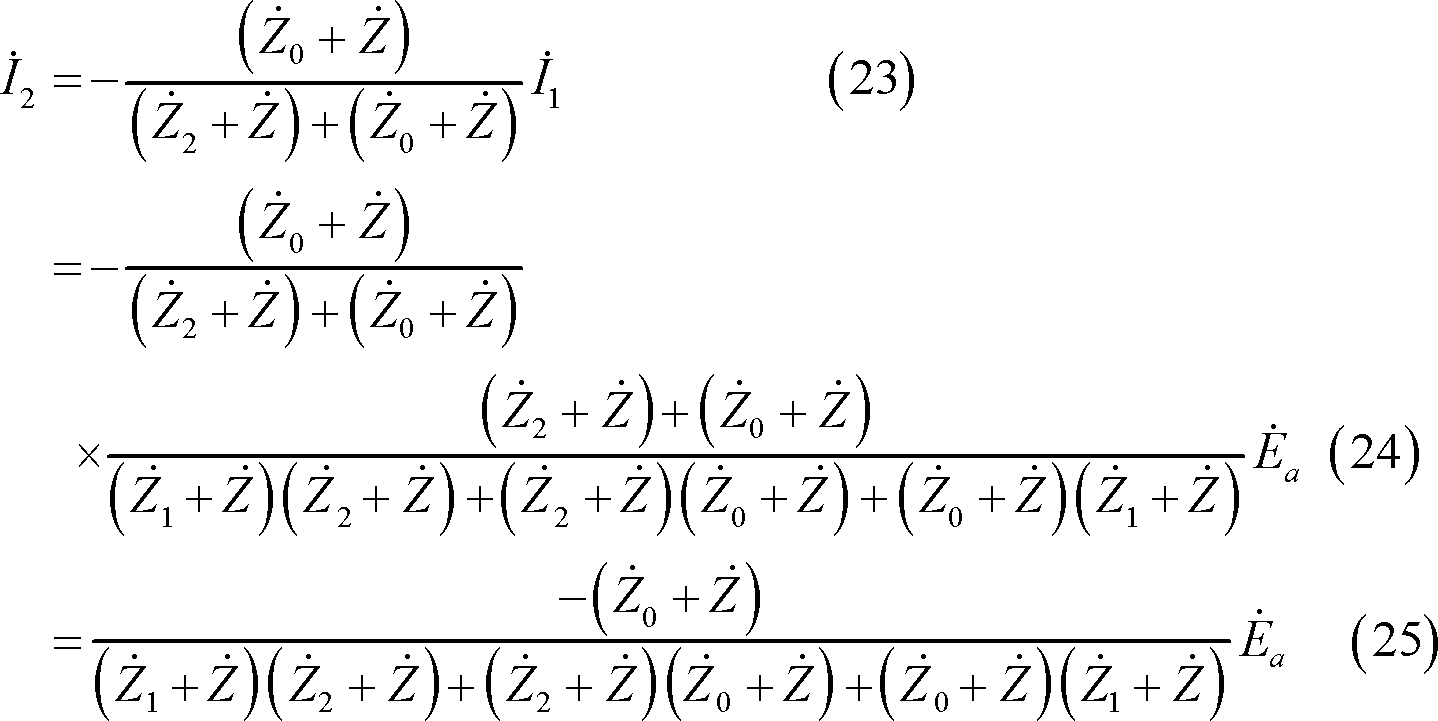
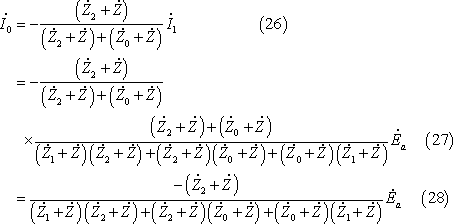
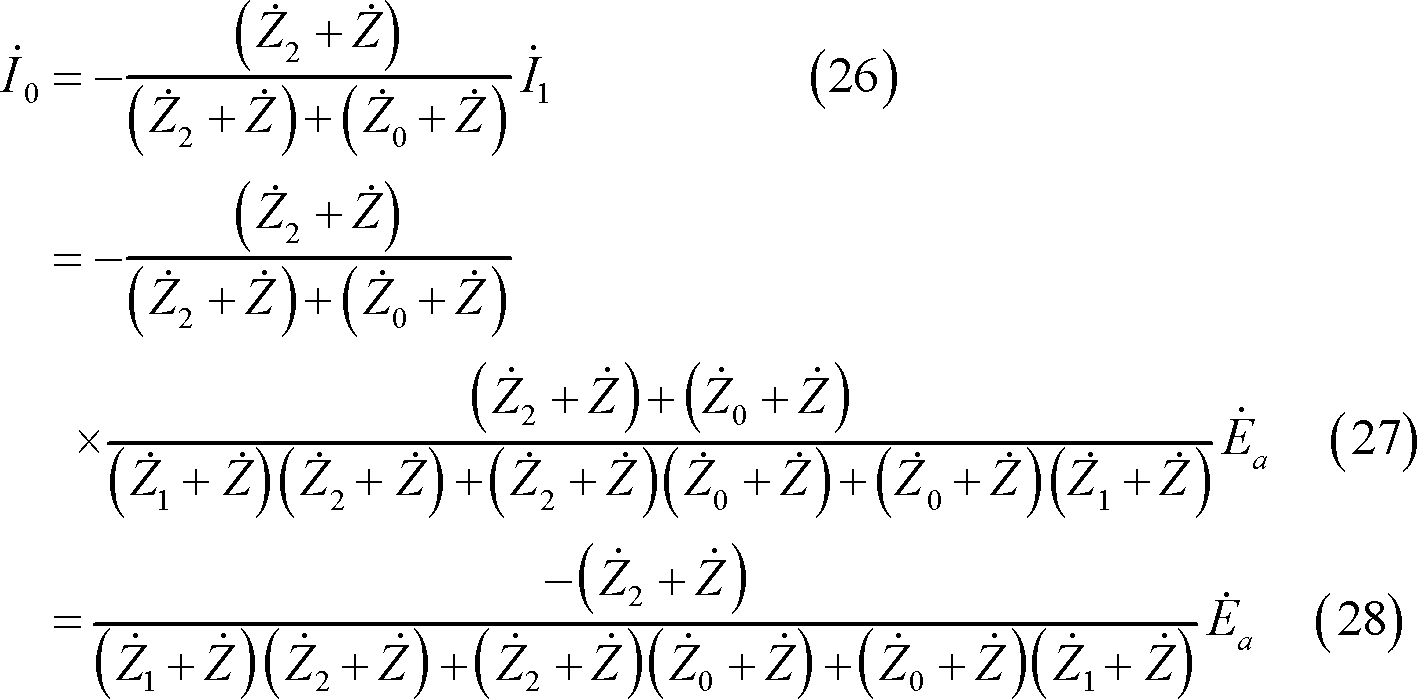
*** 4 逆変換 ***********************************************
各相の電流は、
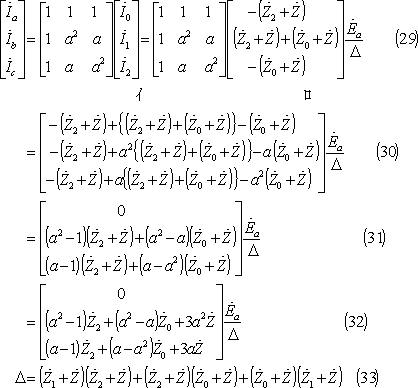
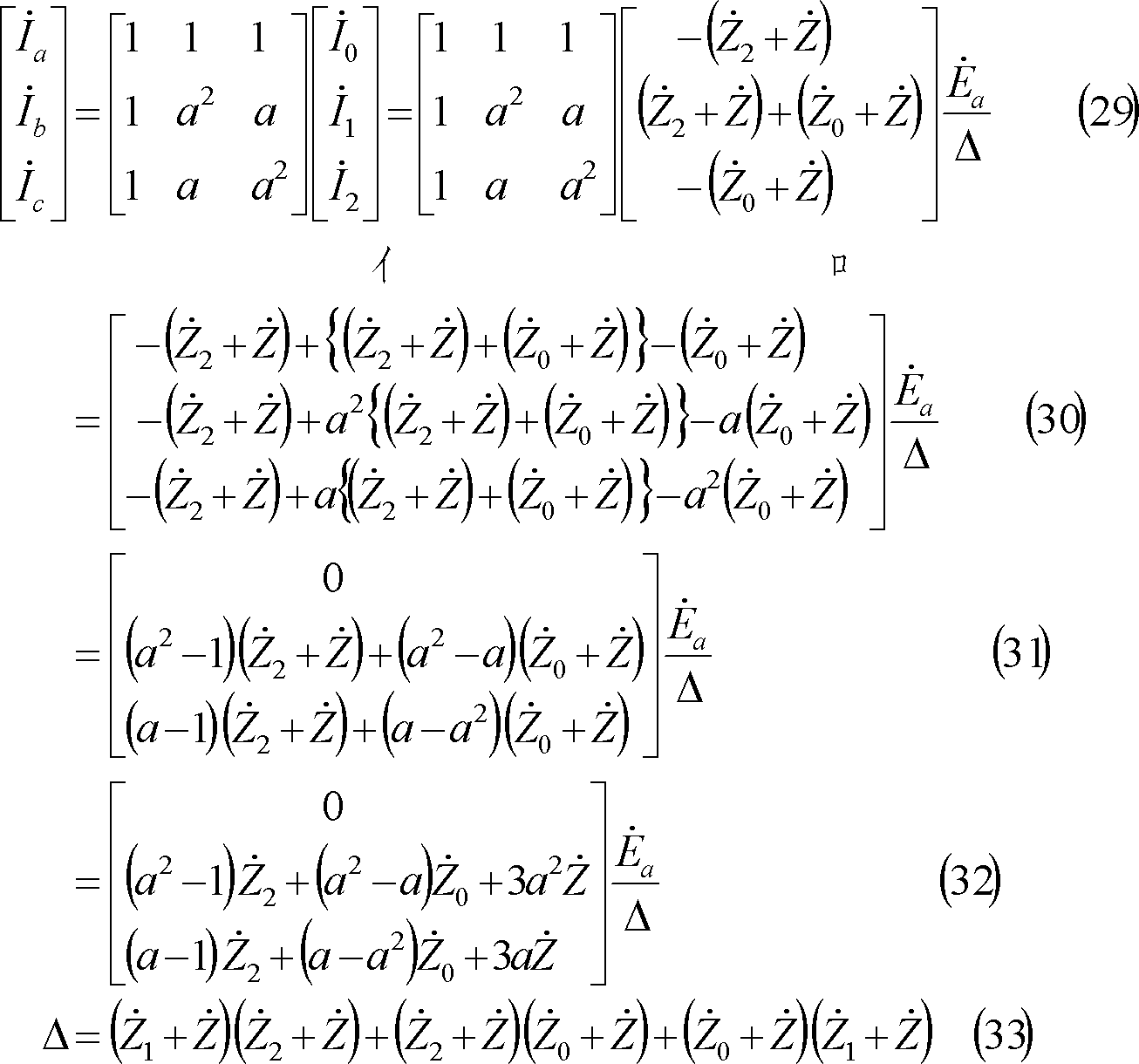
各相の電圧は、
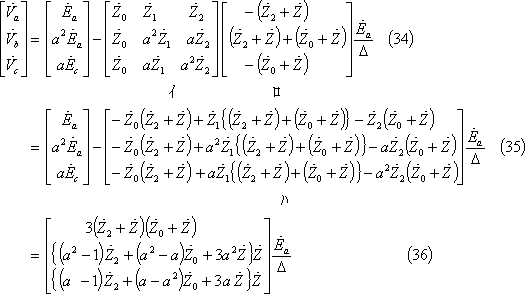
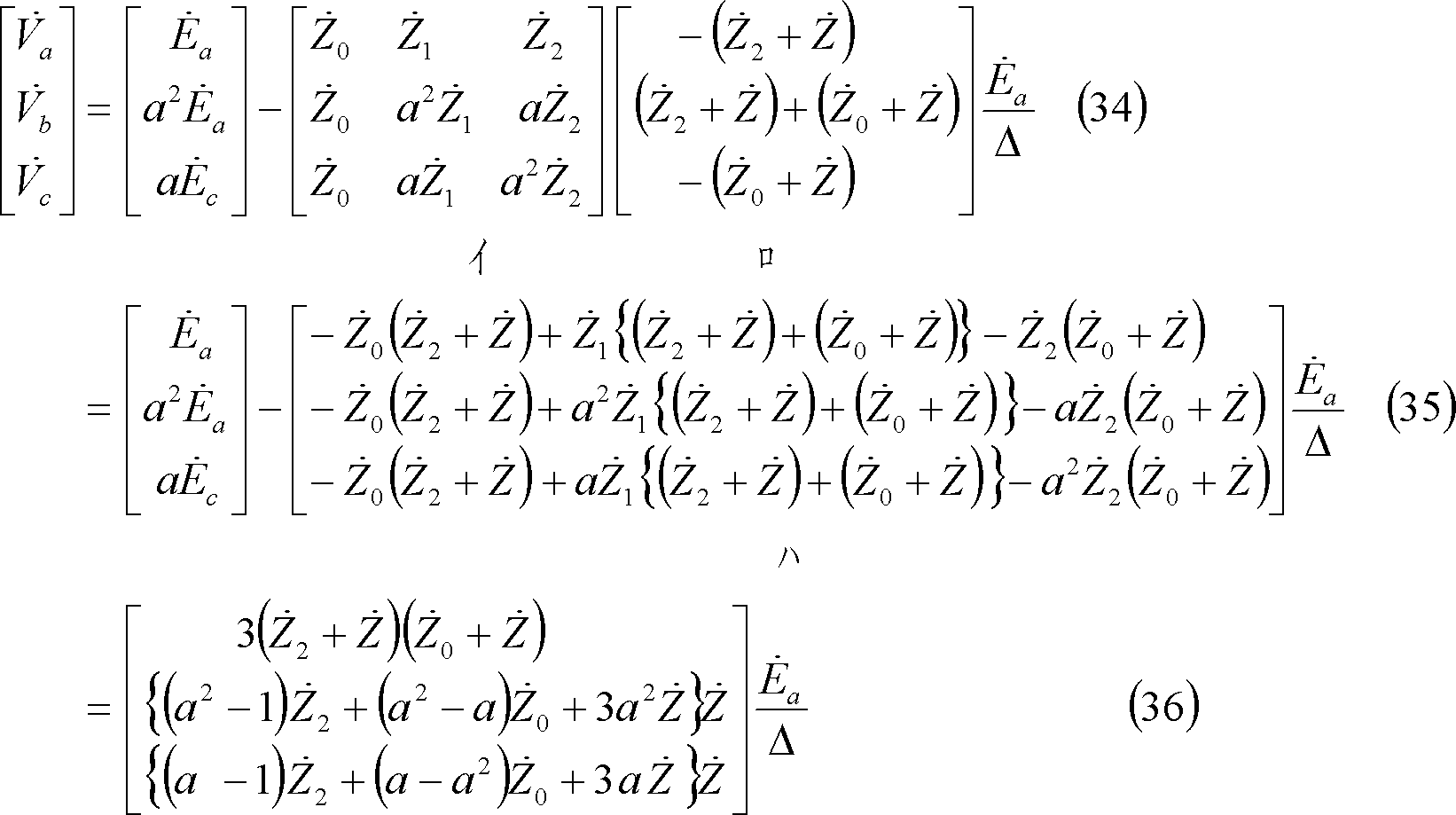
[注] b、c両相の電圧は回路条件式である
![]()
![]() から求めることもできる。
から求めることもできる。
第16図の回路のようにa相端子、b相端子、c相端子の3端子が短絡し、それが
![]()
![]() を通して地絡したときの地絡電流及び発電機端の電圧を求めてみよう。
を通して地絡したときの地絡電流及び発電機端の電圧を求めてみよう。
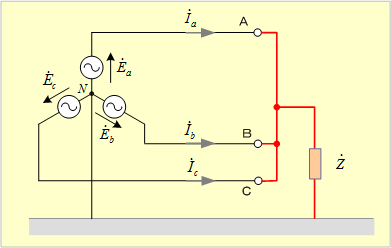

第16図 三相短絡インピーダンス地絡回路
*** 1 回路条件 *********************************************
*** 2 対称分変換 ********************************************
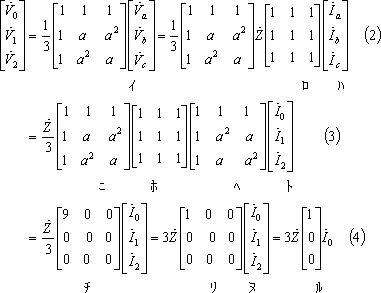
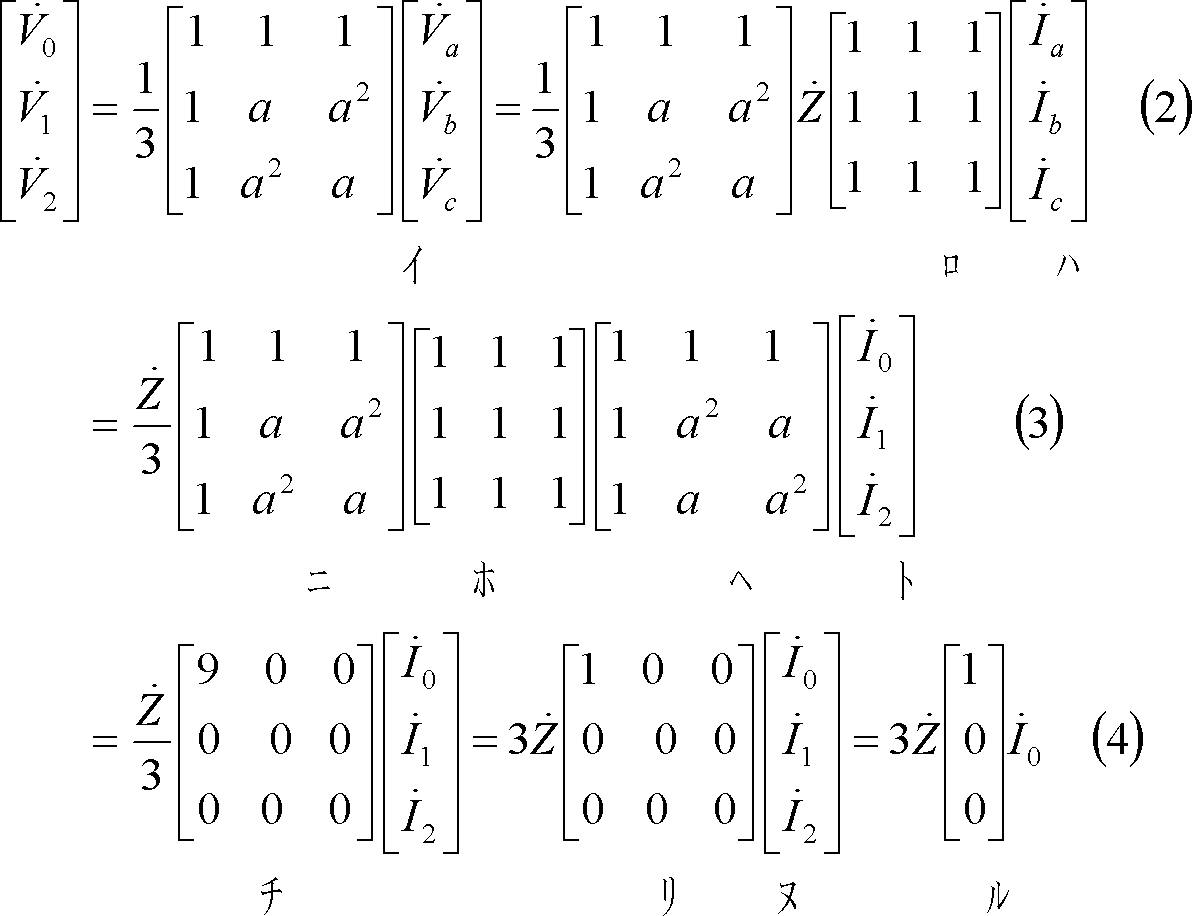
*** 3 対称分回路計算 ***************************************
発電機の基本式と(4)式を等値して、
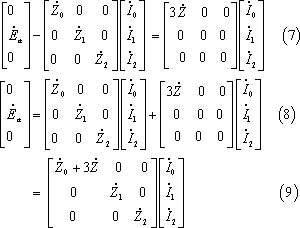
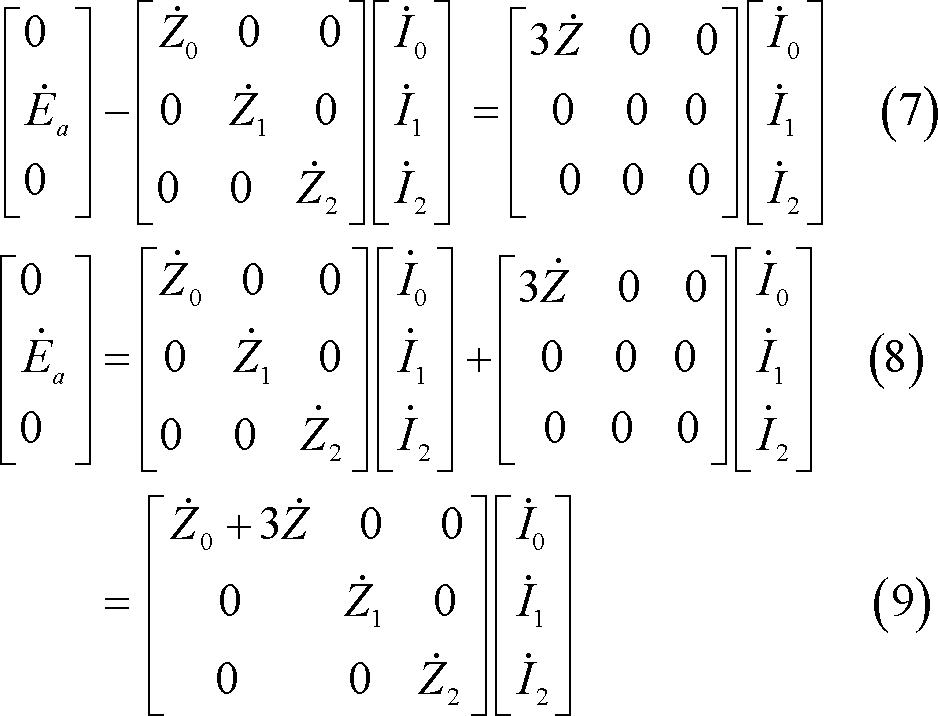
上式の第1行から(10)式、第3行から(11)式が成立し、
![]()
![]() であり、第2行から(12)式が成立し、
であり、第2行から(12)式が成立し、
![]()
![]() は(13)式となる。
は(13)式となる。
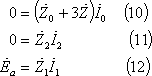
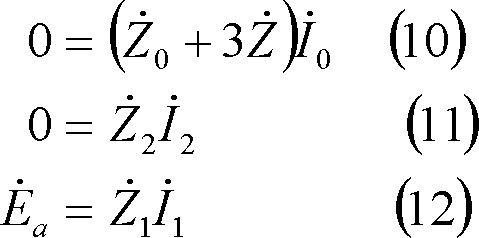
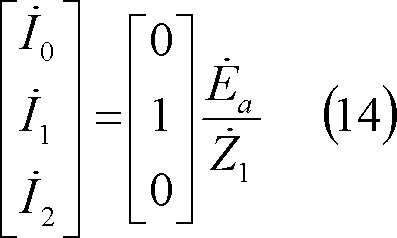
なお、三相短絡インピーダンス地絡回路の対称分回路は、第(10)、(11)、(12)の式より、第17図となる。
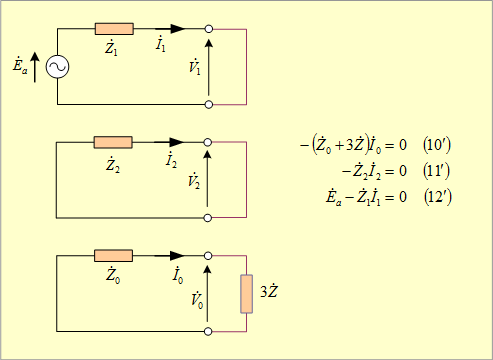

第17図 三相短絡インピーダンス地絡回路の対称分回路
*** 4 逆変換 ***********************************************
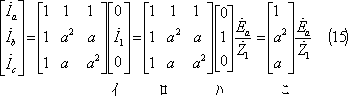
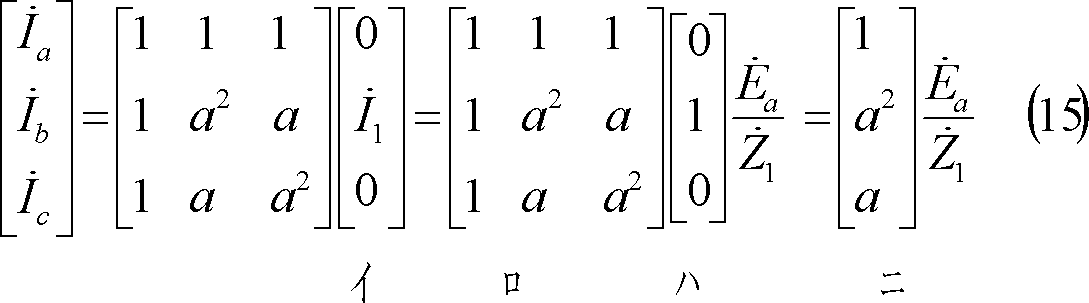
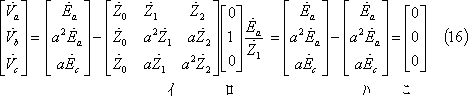
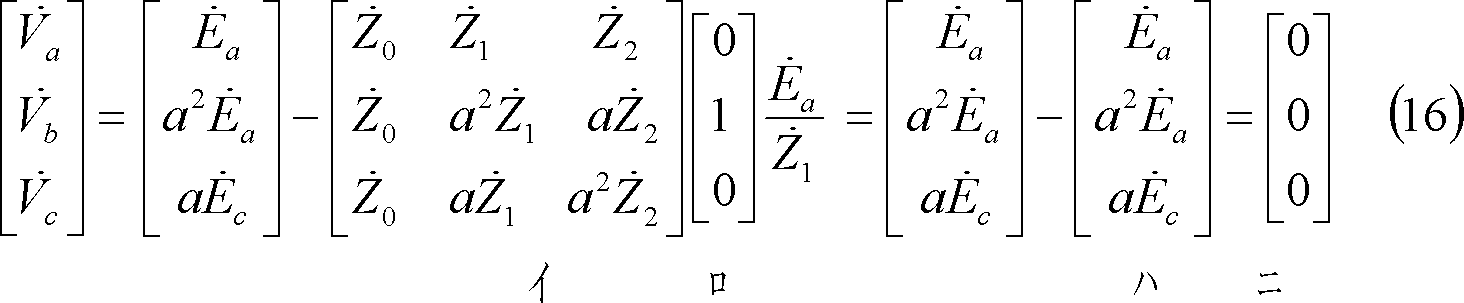
[1]計算の流れ
地絡回路では一般的に零相回路が入ってくる。
(1)回路条件 回路における電圧、電流、電圧電流相互、の関係を式で表す
(2)対称分変換 ① 電流の変換 I’=CI
② 電圧の変換 V’=CV
③ 電流と電圧の相互変換 V=ZIの場合は、
V’=Z’I’ 、ここに、 Z’=CZC-1
④ 電圧方程式
(3)対称分回路計算
(4)逆変換 ① 電流の逆変換を行うI=C-1I’
② 電圧の逆変換を行うV=C-1V’
