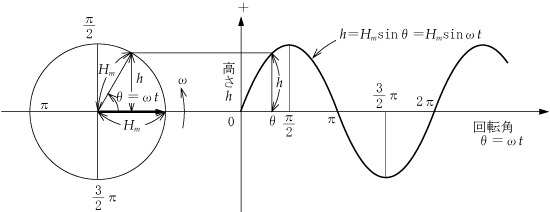
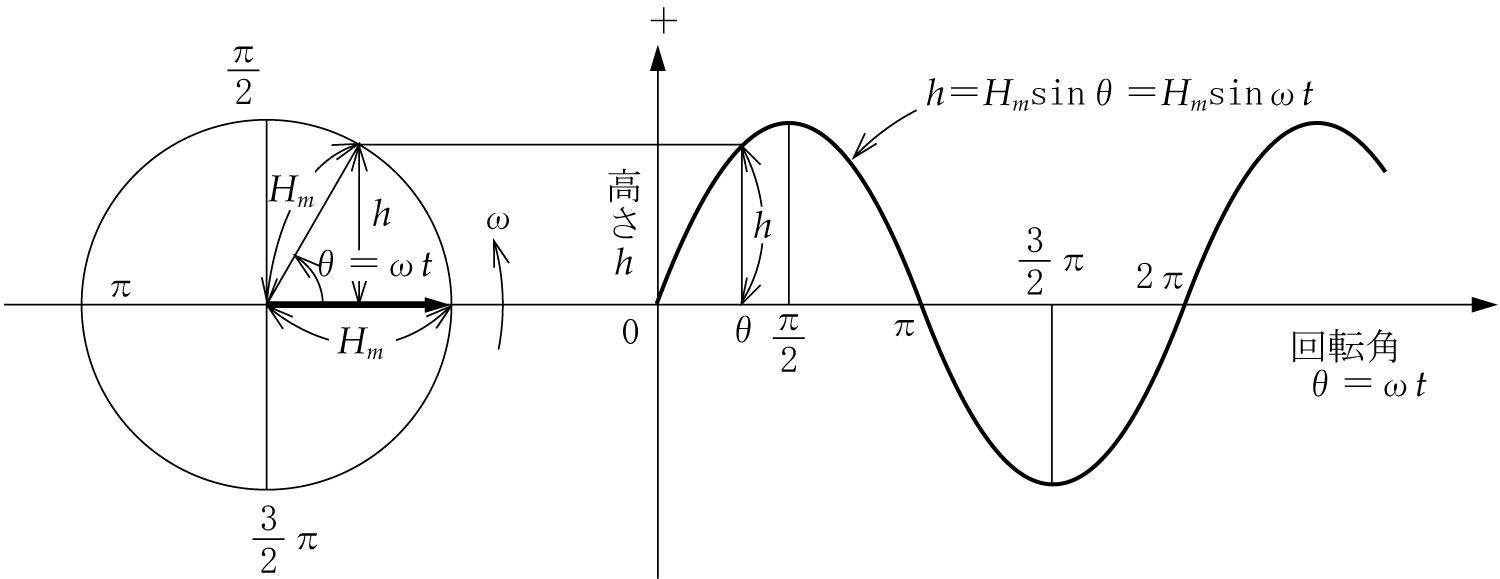
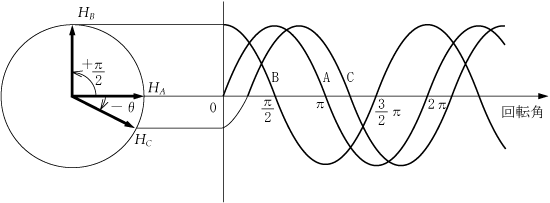
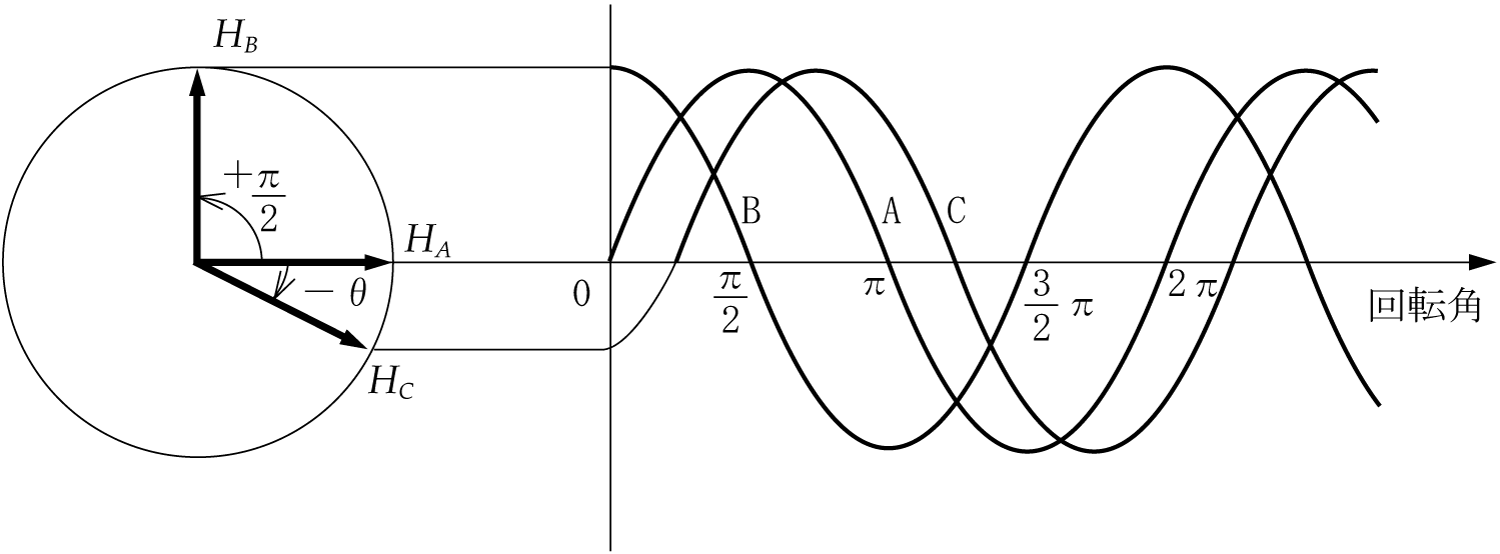
正弦波交流回路の電圧、電流は、本来、瞬時値計算しなければならないが、定常状態に限って言えば、系統各部の電圧、電流の大きさの比、位相差は一定である。この性質を利用することにより、正弦波交流回路の瞬時値をベクトルに置き換えれば計算が簡単になる。ここでは、瞬時値のベクトル表現と複素平面での表示方法を解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your
Flash plugin.
※テキスト中の図はクリックすると大きく表示されます

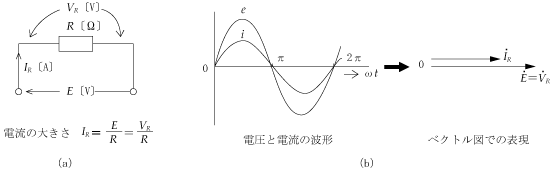
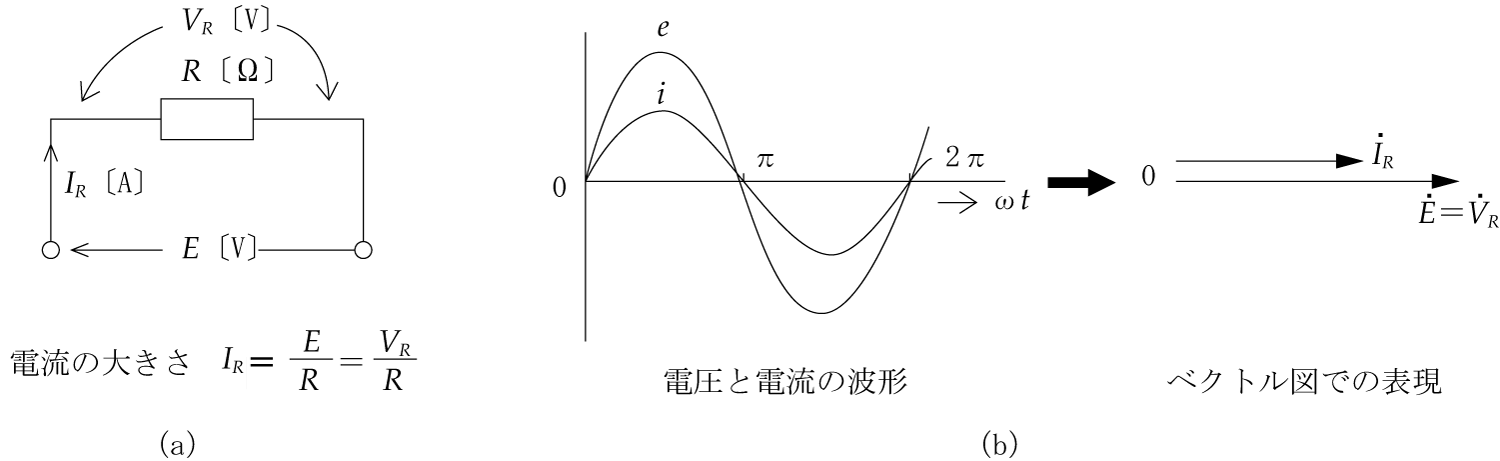
交流回路で取り組まなければならない主な計算は、抵抗、コイル、コンデンサなどの素子が組み合わさった回路に正弦波交流電圧を加えたとき、回路にどのような電流が流れるか、あるいは素子の端子間にどのような電圧が生ずるか、また発生する電力はいくらかなどを調べることが中心となる。
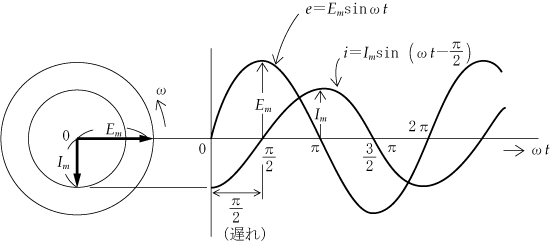
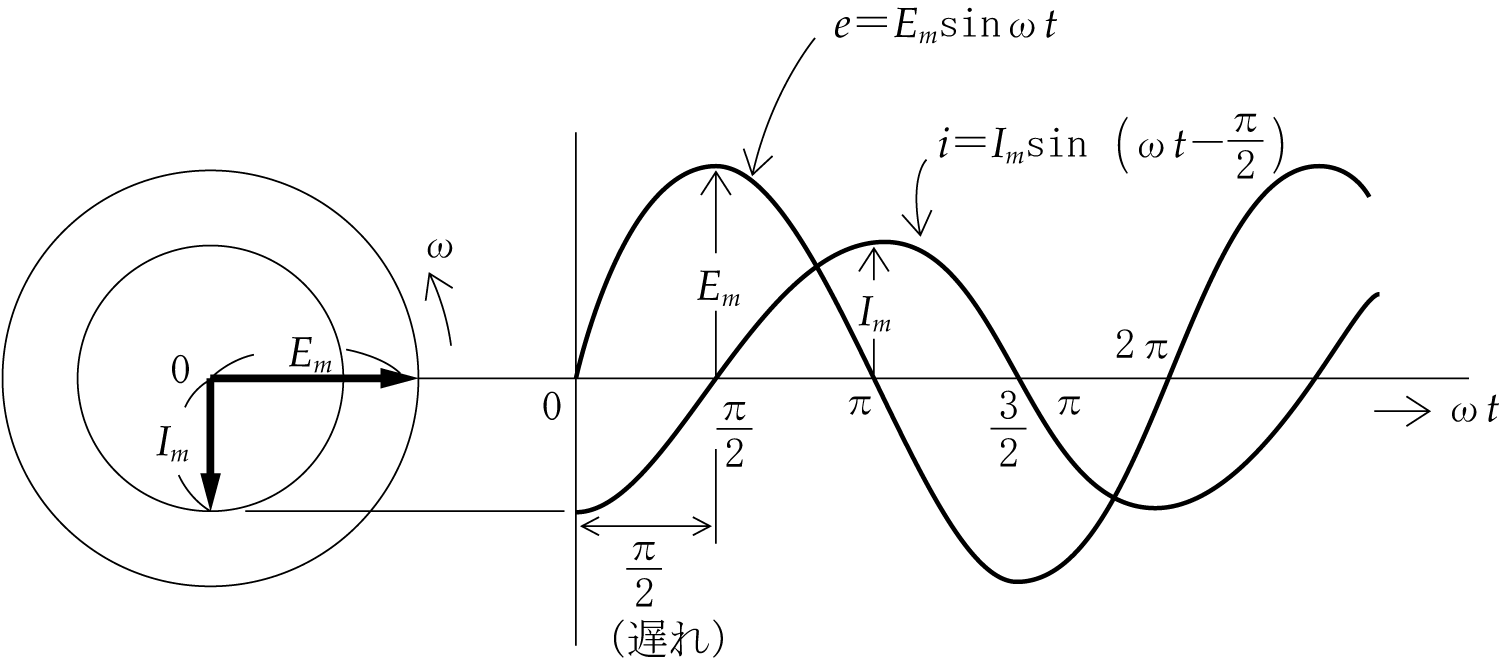
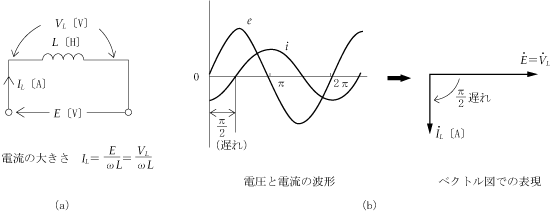
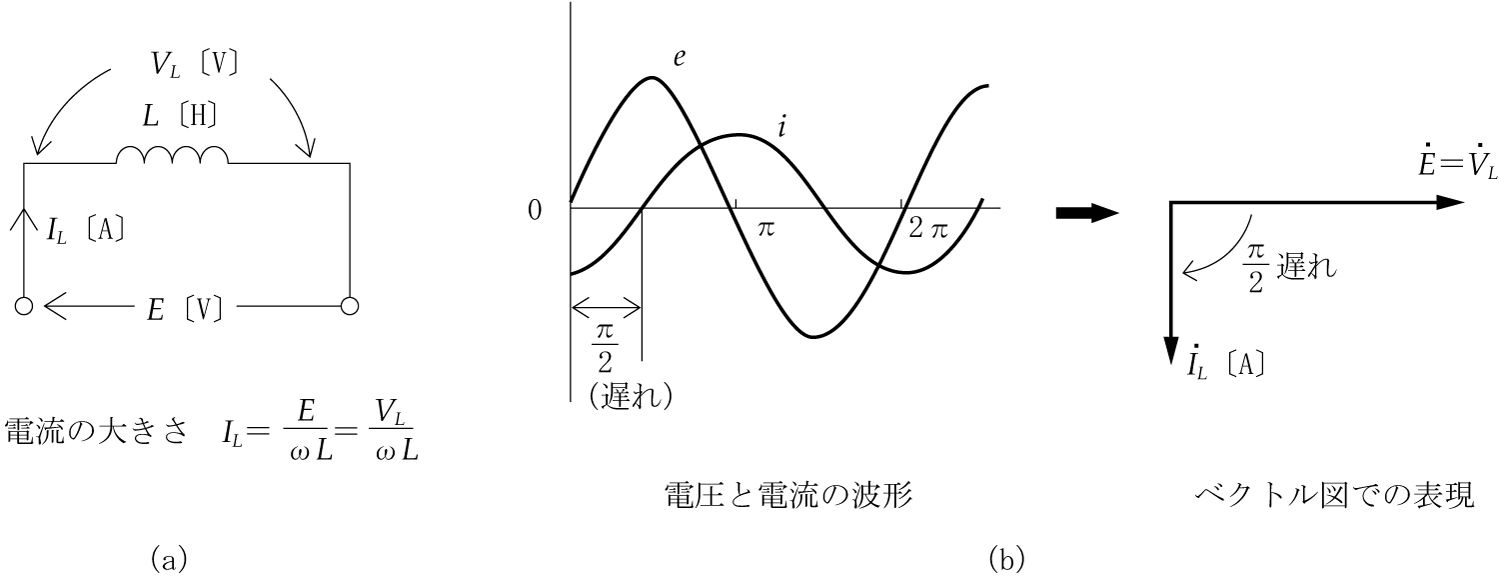
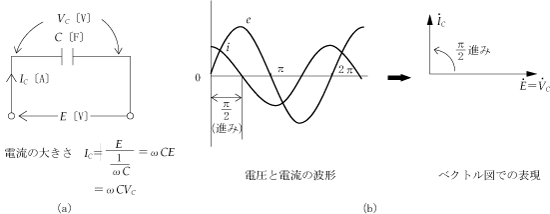
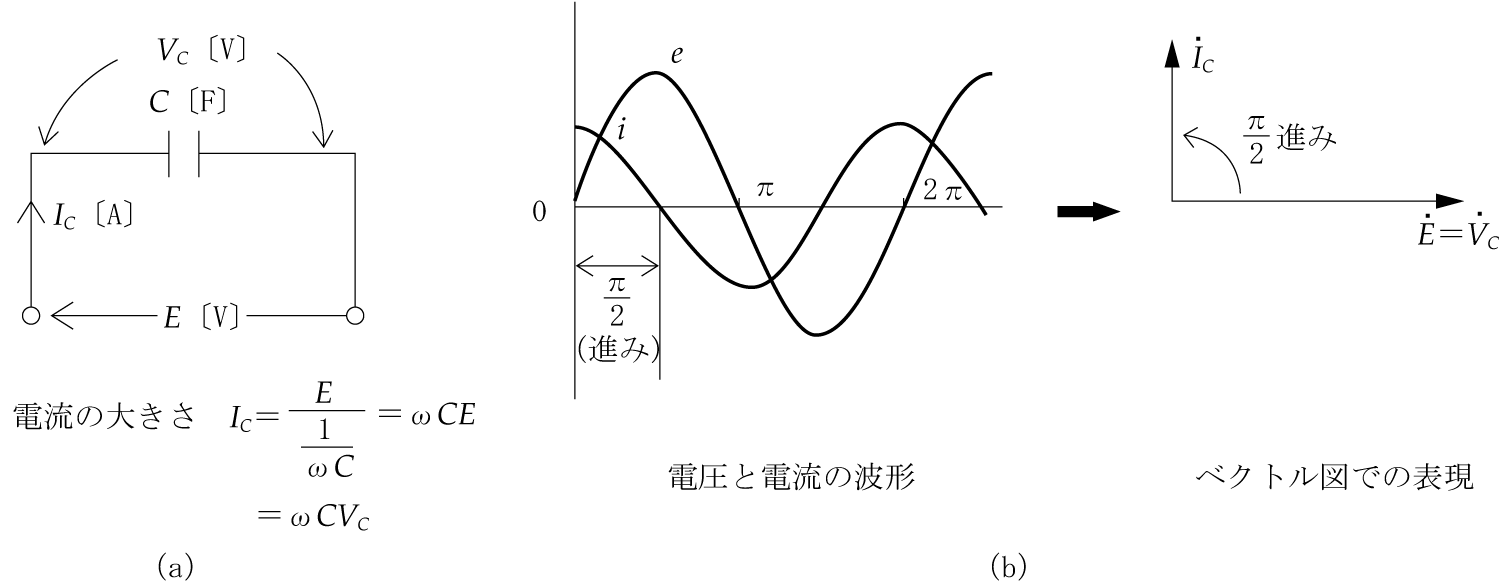
ここで主役は電源となる正弦波交流電圧であるが、一般的に回路に加えた電源電圧の波形と、回路に流れる電流の波形とは重なり合うことはなく、進みあるいは遅れのずれが生じている(位相差がある)。このことが直流回路の計算と比べてみると、交流回路の計算を面倒にしている。
このように交流回路では、電流と電圧の波形のずれがあるため、このことを考慮して計算の中で取り扱わないと、矛盾が生じて正しい答は得られない。
どのように考慮すればよいのかということになるが、一つの方法は、電圧や電流をベクトルに変換するというテクニックを使うことである。つまり、ベクトル計算という手法を用いることによって、瞬間瞬間に大きさや方向が変化する複雑な交流波形を簡単化してしまうのである。いわばベクトルは交流波形のプロフィール(横顔)による処理というわけである。