〜終わり〜
■ぜひアンケートにご協力下さい■


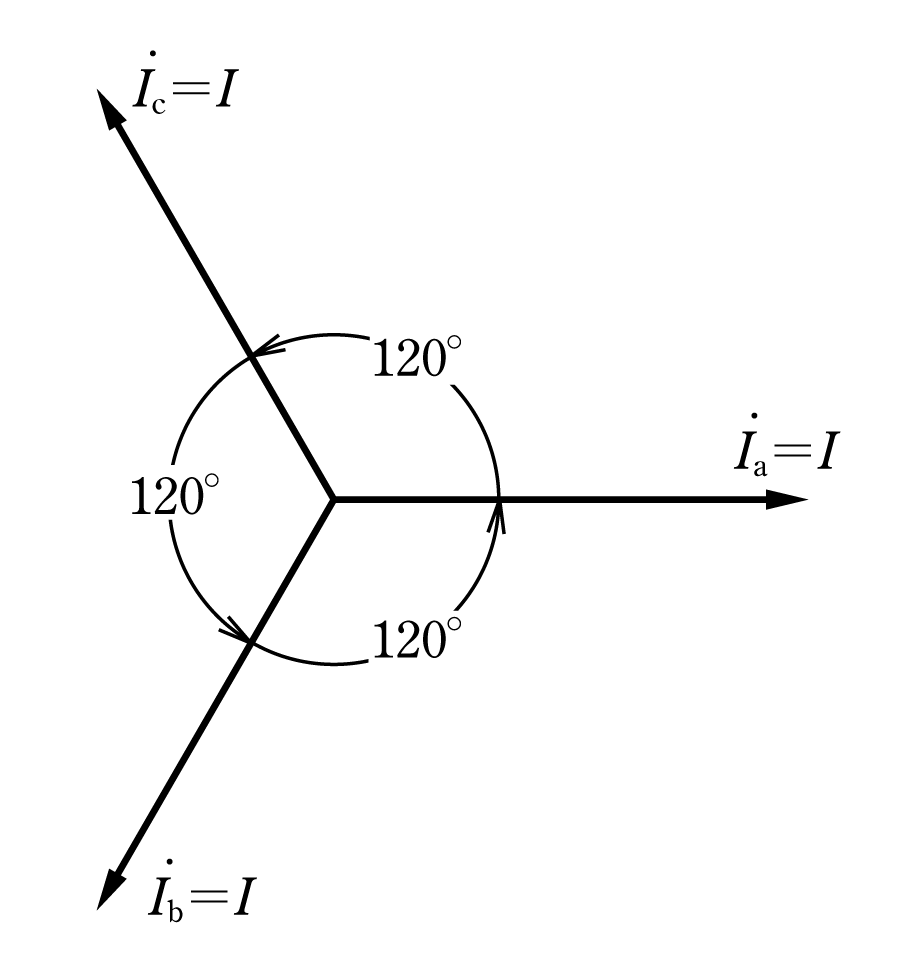
第1図は三相交流電流のベクトル図を示したものであるが、それぞれのベクトルは、
![]()
![]() は
は
![]()
![]() より120°位相が遅れ、
より120°位相が遅れ、
![]()
![]() は
は
![]()
![]() より120°(
より120°(
![]()
![]() からは240°)遅れており、お互いの関係は第2図のようにして知ることができる。
からは240°)遅れており、お互いの関係は第2図のようにして知ることができる。
次に第2図のcosθ+jsinθの値を計算し、もっと具体的な数字を調べることにする。
![]()
![]() また
また
![]()
![]() であるから、
であるから、
ということになる。そうすると、
![]()
![]() は
は
![]()
![]() より120°位相が進んでいるから、
より120°位相が進んでいるから、
になることが分かる。また、
![]()
![]() は
は
![]()
![]() より120°位相が進んでいるから、
より120°位相が進んでいるから、
となることが分かる。
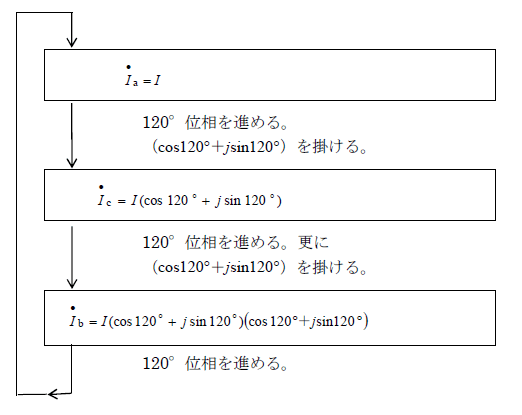
第2図
ここで
![]()
![]() とおくことにすると、
とおくことにすると、
![]()
![]() と
と
![]()
![]() の関係は次のとおりになる。
の関係は次のとおりになる。
![]()
![]() 、
、
![]()
![]() 、
、
![]()
![]()
このように三つの電流のベクトルの関係を、実に簡単な複素数を使って表すことができてしまうので、この式のaやa2を作用子またはベクトルオペレータと呼んでいる。ちょうど単相交流回路でjがベクトルの位相を90°変化させる作用をするのと同様な意味で、三相交流回路ではベクトル
![]()
![]() に順々に
に順々に
![]()
![]() を掛けることによって、大きさは
を掛けることによって、大きさは
![]()
![]() と同じで、ただ120°位相が進むことになる。
と同じで、ただ120°位相が進むことになる。
![]()
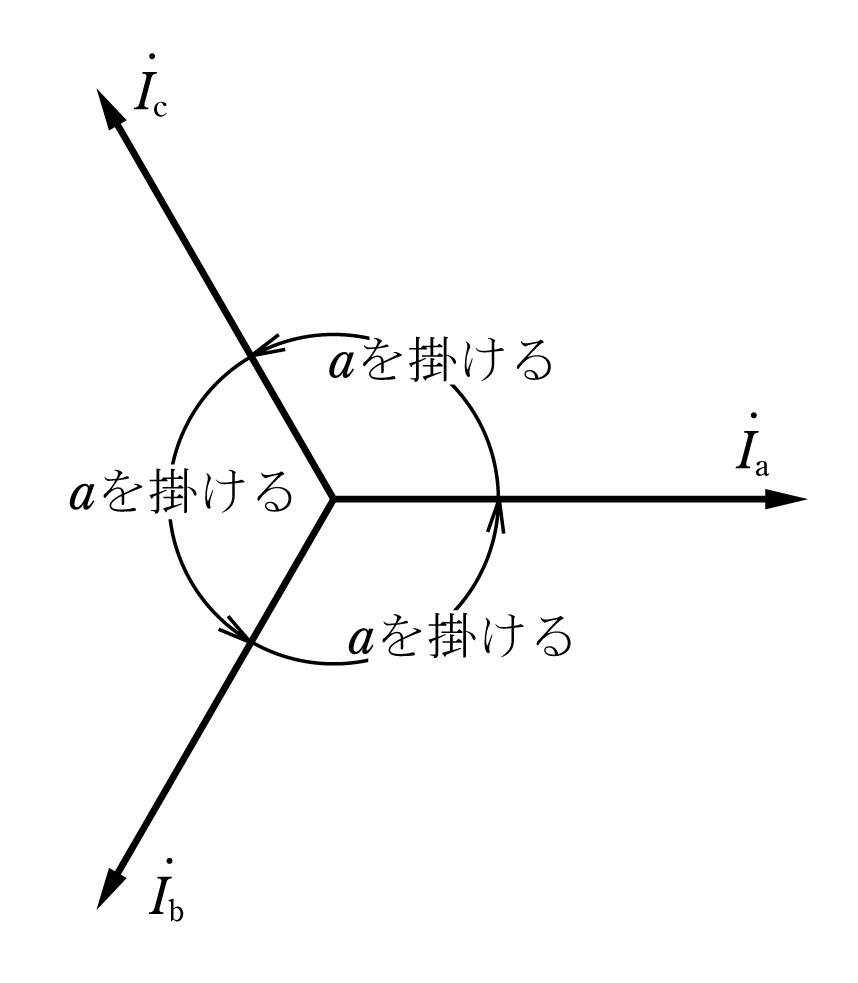
![]() をベクトルオペレータと呼ぶのは、第3図のようにベクトルの運転手であるというイメージからきている。
をベクトルオペレータと呼ぶのは、第3図のようにベクトルの運転手であるというイメージからきている。
さて、三相交流の三つのベクトルはベクトルオペレータを使えば、簡単に表現できることを知ったが、では
![]()
![]() をどのような方法で問題の解答に生かしていけばよいか、具体的に調べることにしよう。
をどのような方法で問題の解答に生かしていけばよいか、具体的に調べることにしよう。
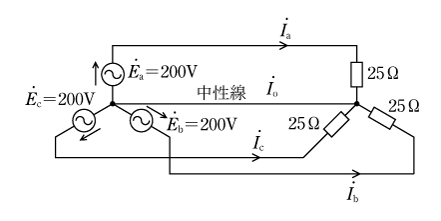
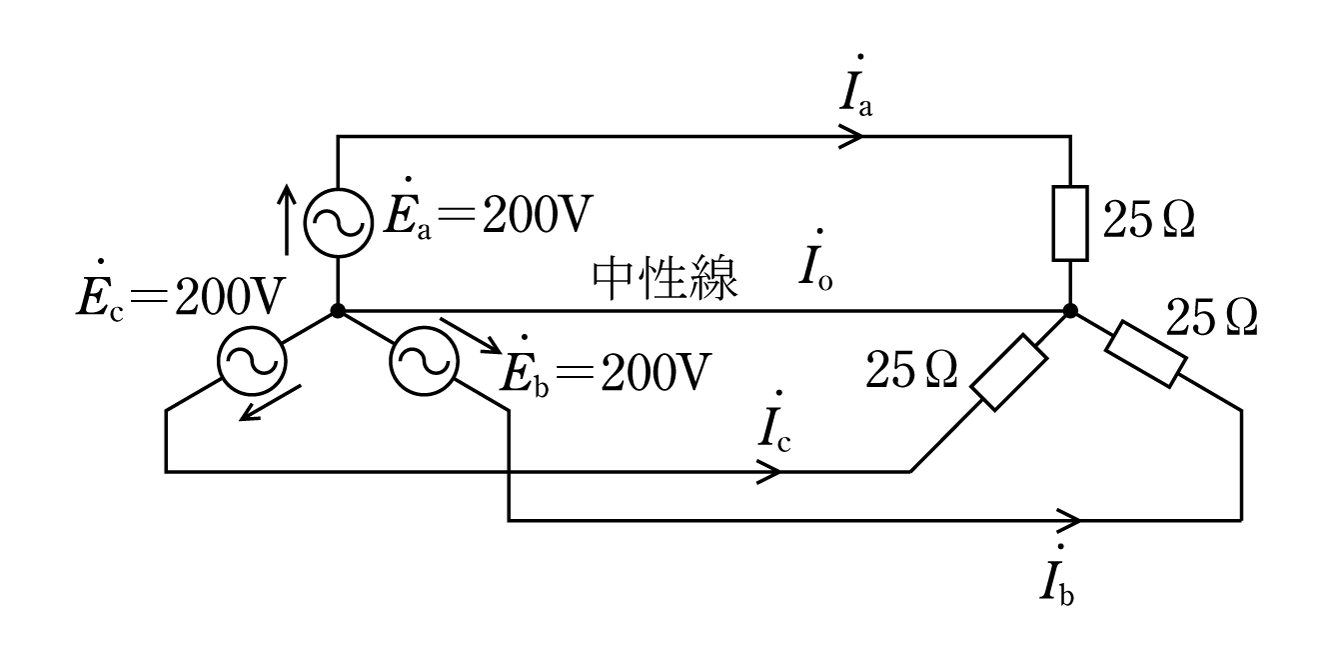
第4図の平衡三相回路では中性線に電流が流れないので、このようにわざわざ中性線を書き込むことはないが、初めにベクトルオペレータaを使って中性線電流が0になることを確認してみよう。
〔問題〕 次の三相平衡回路における電流I0を求めよ。
〔正解〕
![]()
![]() すなわち、各相を流れる電流はいずれも8Aになる。したがって、中性線を流れる電流
すなわち、各相を流れる電流はいずれも8Aになる。したがって、中性線を流れる電流
![]()
![]() は、
は、
![]()
![]() 、
、
![]()
![]() 、
、
![]()
![]()
であるから、
〔答〕 電流
![]()
![]()
![]()
![]() A
A
〔落とし穴〕
![]()
![]() 、
、
![]()
![]() 、
、
![]()
![]() とおき、
とおき、
この場合、答は合っていても、
![]()
![]() 、
、
![]()
![]() であることを間違えてはいけない。
であることを間違えてはいけない。
![]()
![]() や
や
![]()
![]() がどのベクトルにかかっているかを、しっかりつかんでおくことが大切である。
がどのベクトルにかかっているかを、しっかりつかんでおくことが大切である。
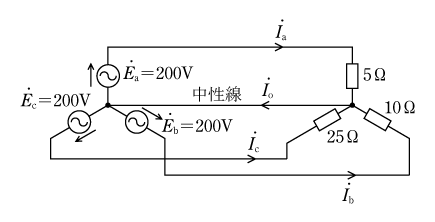
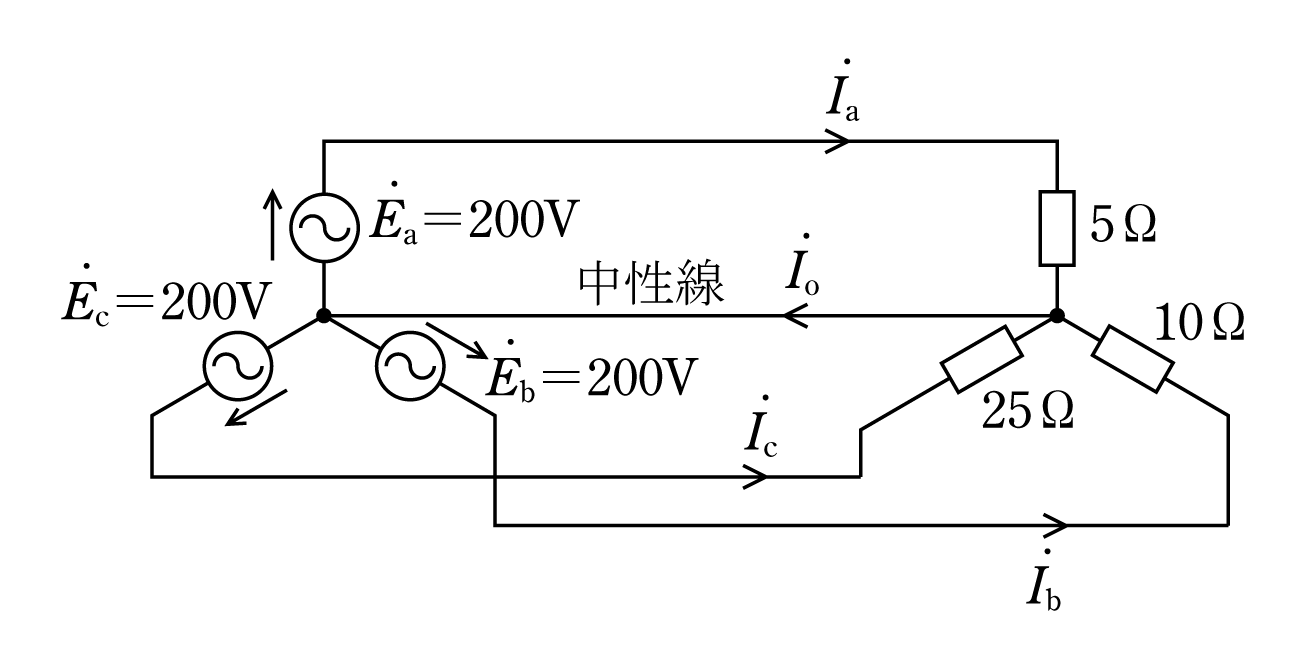
次の第5図の問題は
![]()
![]() の力で正解へ導いてくれる。前問とよく似ているが、ここでは負荷抵抗の値がそれぞれ異なる不平衡回路なので、発電機側で平衡三相交流を発電・供給していても、負荷側の電流の大きさは異なり、そのため中性線にも電流が流れてしまう。
の力で正解へ導いてくれる。前問とよく似ているが、ここでは負荷抵抗の値がそれぞれ異なる不平衡回路なので、発電機側で平衡三相交流を発電・供給していても、負荷側の電流の大きさは異なり、そのため中性線にも電流が流れてしまう。
![]()
![]() を活用することで、この電流を求めることができる。
を活用することで、この電流を求めることができる。
〔問題〕 次に示す不平衡負荷回路における
![]()
![]() の大きさを求め、
の大きさを求め、
![]()
![]() と
と
![]()
![]() の位相差を求めよ。
の位相差を求めよ。
![]()
![]() がどのベクトルにかかっているか、この問題でも間違えないように計算を進めないといけない。
がどのベクトルにかかっているか、この問題でも間違えないように計算を進めないといけない。
次のような手順で解答していく。
① まず
![]()
![]() の大きさを求める。
の大きさを求める。
![]()
![]() A、
A、
![]()
![]() A、
A、
![]()
![]() A
A
②
![]()
![]() を
を
![]()
![]() を使って表現する。
を使って表現する。
③
![]()
![]() を計算する。
を計算する。
④
![]()
![]() の絶対値を求める。
の絶対値を求める。
I 0 = 28A
⑤
![]()
![]() と
と
![]()
![]() との位相差(偏角)を求める。
との位相差(偏角)を求める。
![]()
![]() から θ=24°(三角関数表から)
から θ=24°(三角関数表から)
この問題では中性線が結ばれており、この中性線を流れる電流をベクトルオペレータ
![]()
![]() を用いて解いたが、三相の負荷インピーダンスが異なる不平衡回路で中性線が結ばれていない場合には、たとえ電源は平衡三相電圧であったとしても簡単に計算を進めていくことはできない。このような場合の
を用いて解いたが、三相の負荷インピーダンスが異なる不平衡回路で中性線が結ばれていない場合には、たとえ電源は平衡三相電圧であったとしても簡単に計算を進めていくことはできない。このような場合の
![]()
![]() の扱い方については別の機会に取り上げたいと思う。
の扱い方については別の機会に取り上げたいと思う。