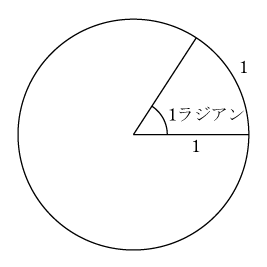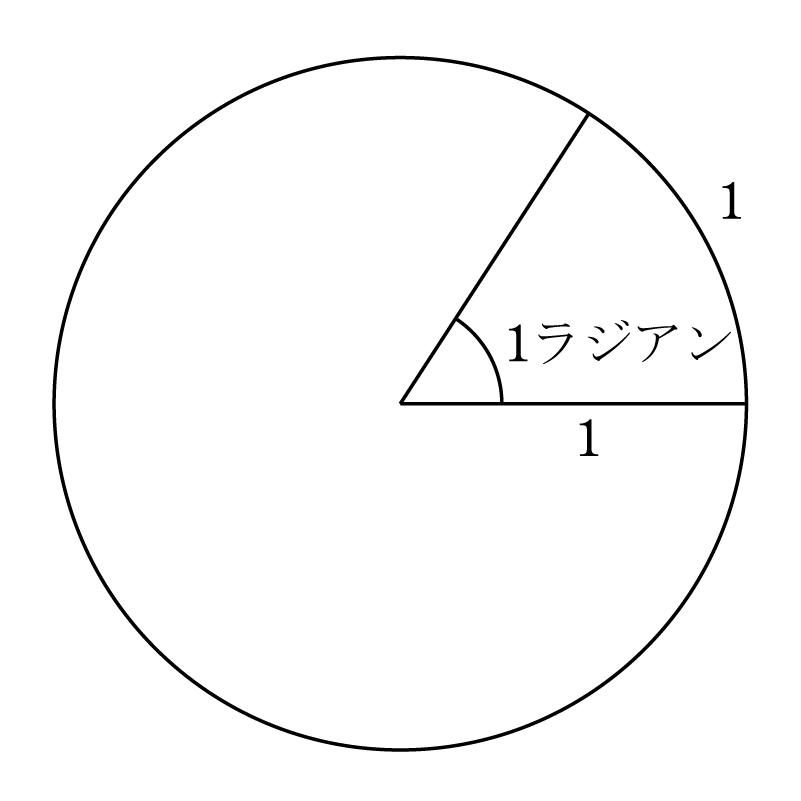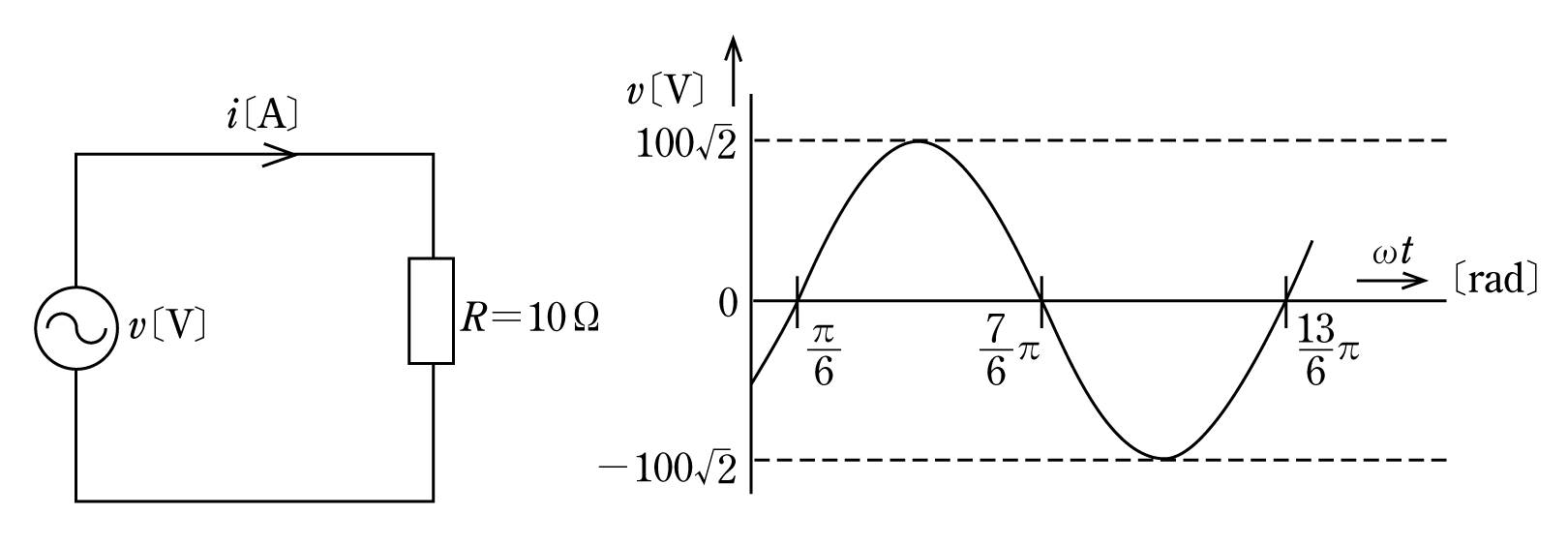〜終わり〜
■ぜひアンケートにご協力下さい■


三角関数はsinやcosなど英記号で表すので難しいと思っている人が意外に多いが、正弦波交流を取り扱う上で重要な関数である。ここでは、三角関数のグラフと交流の瞬時値の式を対比させ交流波形を描くこと、瞬時値の式から位相の進み遅れが分かることを目標に解説する。また、関連する電験の過去問題も例題として取り上げ、理解を深めよう。
角の大きさを表すのに、最もふつうに用いられるのは、直角の1/90を単位とする表し方である。この直角の1/90は1度と呼ばれ、記号1°で表される。この単位によれば、直角は90°、平角は180°、円周角は360°となる。
しかし、電気では“度”よりもむしろ弧度法による単位を用いたほうが便利である。この方法は半径が1である円の周の長さが2πであることを利用して、円周角360°が2πで表されるように、単位の角を選ぶのである。
この単位によれば、直角はπ/2で、平角はπで表される。円周角が2πとなるように選んだ角の単位をラジアンまたは弧度という。1ラジアンの角度とは半径1の円において、それを中心角とする円弧の長さがちょうど1に等しくなるような角である(第1図)。
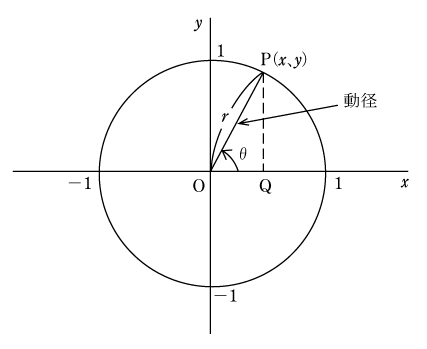
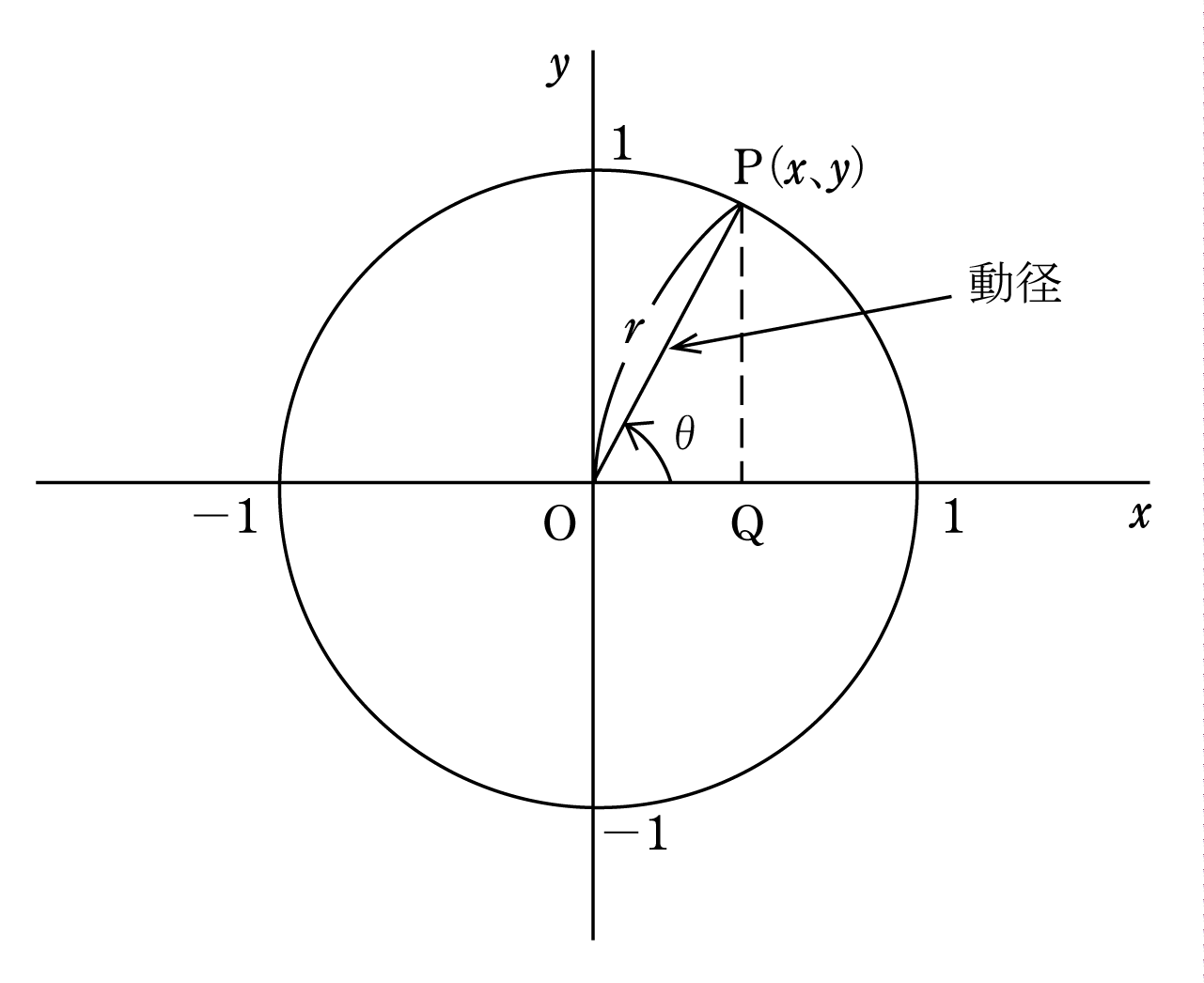
原点Oを中心とする半径1の円を単位円という。第2図でx軸のxの正の部分を始線とする角θの動径と単位円Pとの交点Pの座標(x、y)について考えてみる。OP=1であるから、三角関数の定義から、
OQ/OP =cosθ → x=cosθ PQ/OP=sinθ → y=sinθ
ここで単位円上の点(x、y)について三平方の定理からx2+y2=1
したがって、sin2θ+cos2θ=1となることが分かる。
(1)y=sinθのグラフ
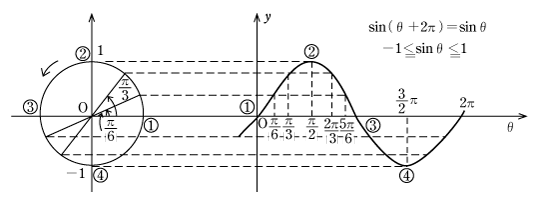
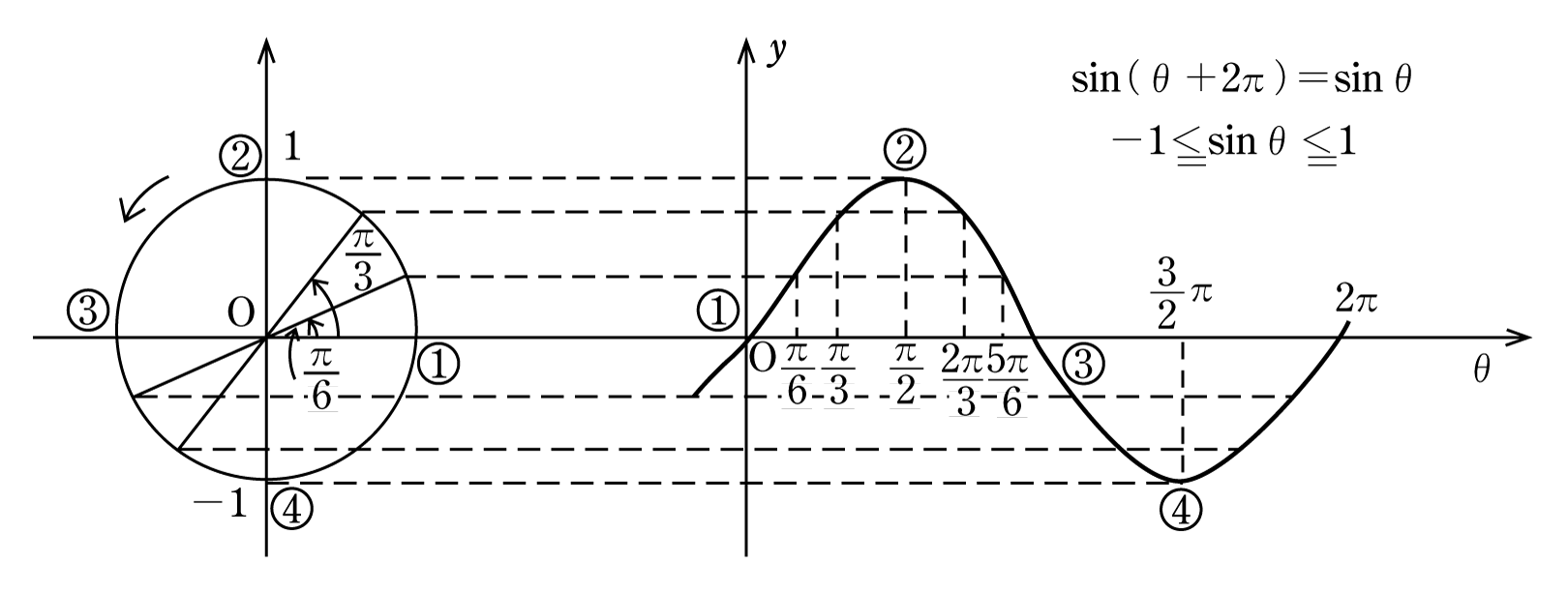
第2図を見てください。Pのy座標がsinθの値になることが分かるはずである。したがって、横軸にθの値をとり、縦軸に各θに対するsinθの値を目盛ってグラフを書くと第3図のようになる。書き方は例えば、右のθ軸上θ=π/6で、θ軸に立てた垂線と、θ=π/6に対する動径と単位円との交点Pからθ軸に引いた平行線との交点をつくる。また、ほかの角度、θ=π/3、π/2、2π/3、5π/6、π、…と順々に同様にして交点をつくり、この交点を結ぶと①、②、③、④のy=sinθのグラフが第3図のようになることが分かる。
これを正弦曲線(サインカーブ)と呼んでいる。また、sinθの値は2π〔rad〕ごとに同じ変化を繰り返す。
(2)y=cosθのグラフ
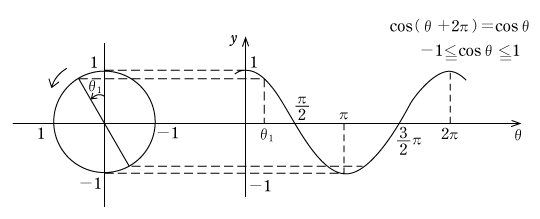
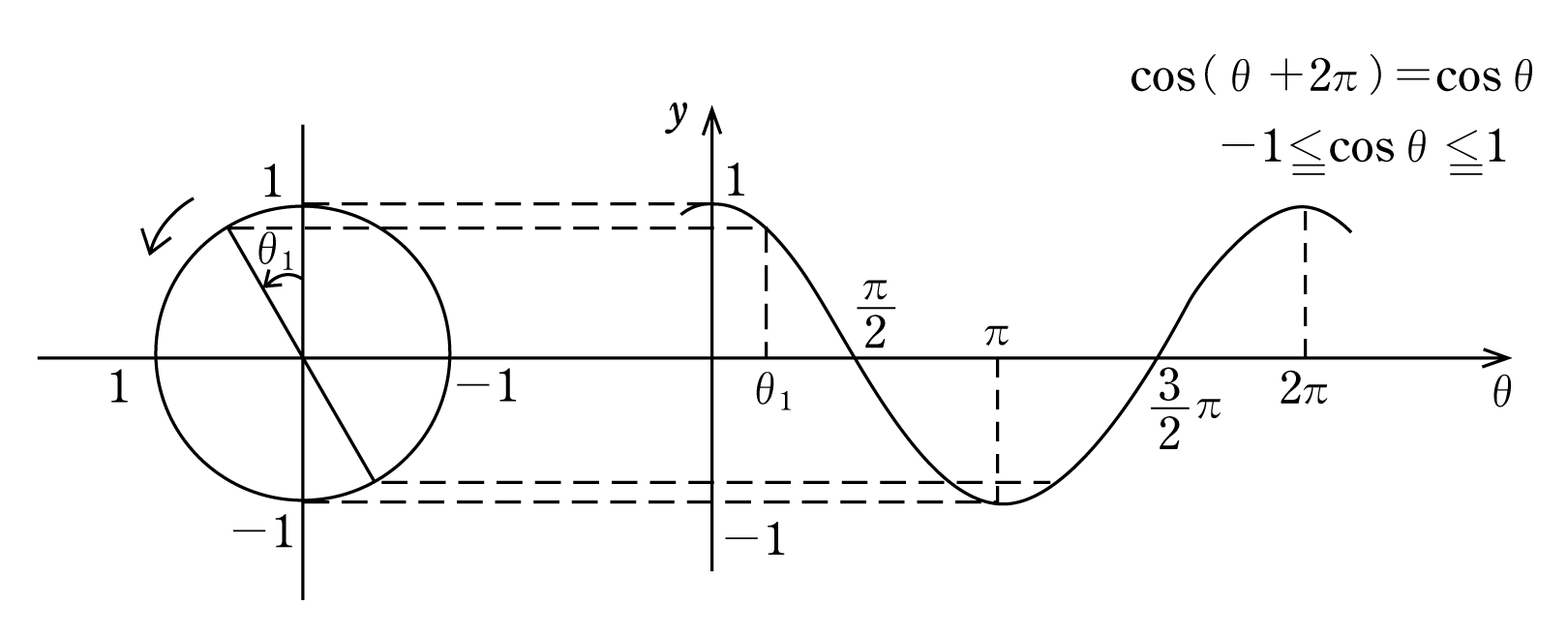
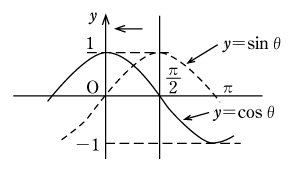
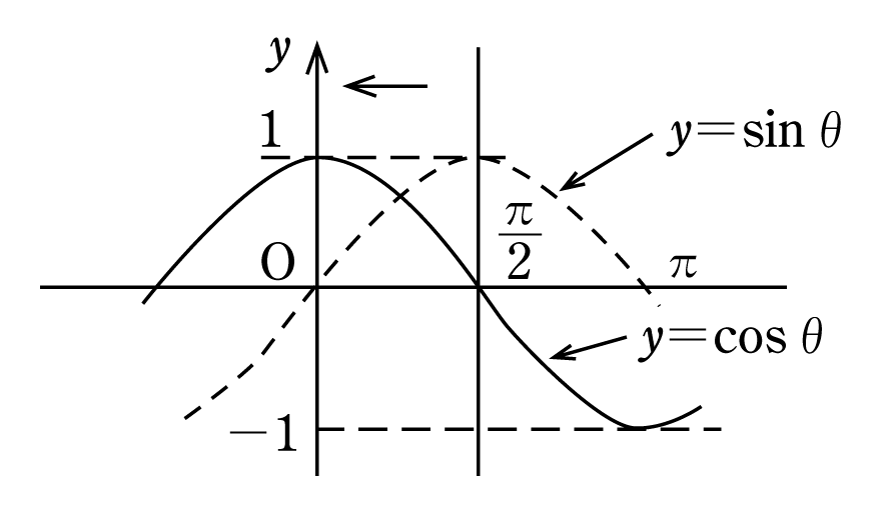
次にy=cosθのグラフを書いてみる。既に第2図で述べたように、角θの動径と単位円との交点をPとすると、Pのy座標がsinθであり、x座標がcosθに等しいことを学んだ。このことから動径Pのx座標の大きさに注目しながら
y=cosθのグラフを書くと、第4図のようになる。y=cosθのグラフは余弦曲線またはコサインカーブと呼ばれる。
しかし、グラフから分かるように cosθ=sin(θ+π/2)であるから、y=cosθのグラフは、y=sinθのグラフをθの方向に-π/2だけ(負の方向にπ/2だけ)平行移動したものである。すなわち、余弦曲線は位置がずれているだけで、形状的には正弦曲線と全く変わりない(第5図)。
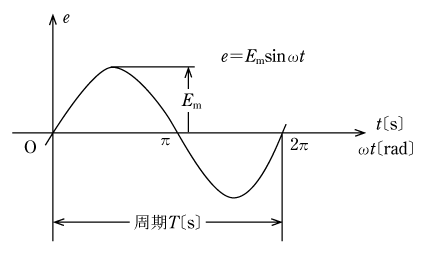
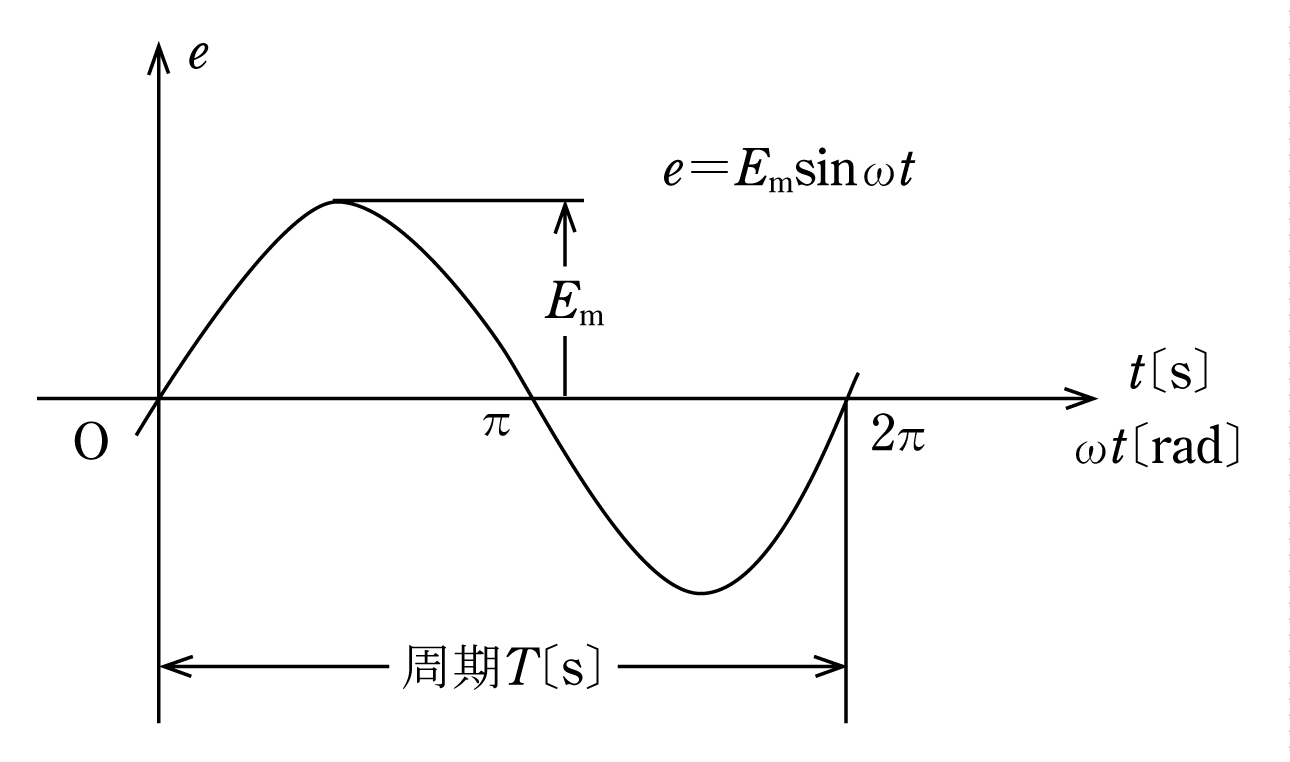
第6図の交流を瞬時値で表現すると、電圧e=Emsinωt〔V〕であるが、Em:最大値であり、実効値をEとすれば
![]()
![]() 〔V〕、またωは角速度〔rad/s〕でω=2πf、θ=ωtである。この交流は時間T〔s〕ごとに同じ変化を繰り返しており、このT〔s〕を周期と呼び、次の関係が成立する。
〔V〕、またωは角速度〔rad/s〕でω=2πf、θ=ωtである。この交流は時間T〔s〕ごとに同じ変化を繰り返しており、このT〔s〕を周期と呼び、次の関係が成立する。
T=1/f〔s〕
三角関数のグラフが二つあった場合、位相の進み遅れの判断が必要となる。このときの判断の基準は交流の波形から行う場合と、瞬時値の式から行う場合がある。いま第7図のように(5・1)式および(5・2)式に示される周波数の等しい二つの波形に時間的なずれ、すなわち位相差があるとき、位相の進み遅れの判断はどうすればよいであろうか。
e1=Emsinωt〔V〕 (5・1)
e2=Emsin(ωt-θ)〔V〕 (5・2)
この二つの交流e1、e2 はt=0のときの位相がそれぞれ0、-θであるから、e1はe2よりもθだけ位相が進んでいる、あるいはe2はe1よりもθだけ位相が遅れていると表現する。また、位相のずれがないときは同相であるという。
e1の位相がe2に対してどれだけ進んでいるか、また遅れているかの判断はe1の位相角からe2の位相角を引けばよい。
(e1の位相角)-(e2の位相角)の値が正の場合は、e1はe2より位相が進んでいることになるし、負ならばe1はe2より位相が遅れていることになる。
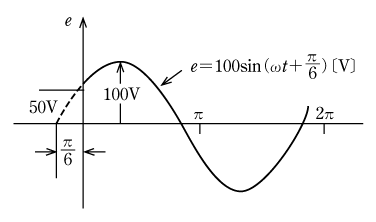
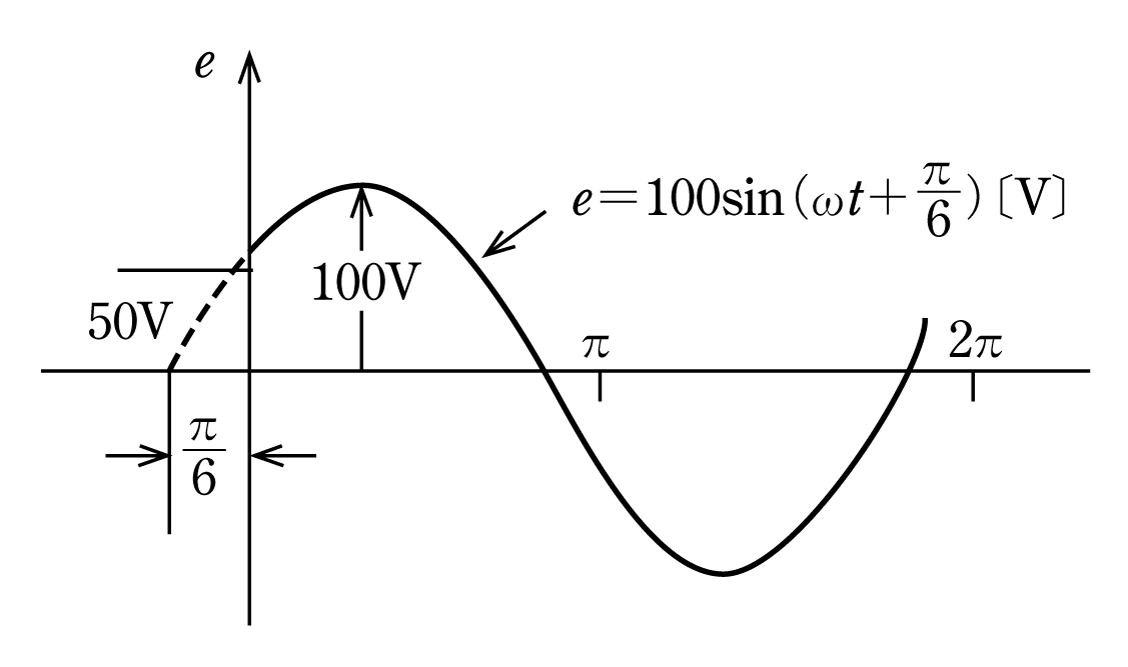
(例題1)e=100sin(ωt+π/6)〔V〕及びi=10sin(ωt-π/3)〔A〕の波形のグラフを描き、eとiとの位相差を求めよ。
〔解答〕 e=100sin(ωt+π/6)において、
ωt=0ではe=100sinπ/6=100×1/2=50V
ωt=-π/6ではe=100sin0=0
となるから、eの波形のグラフは第7図のようになる。
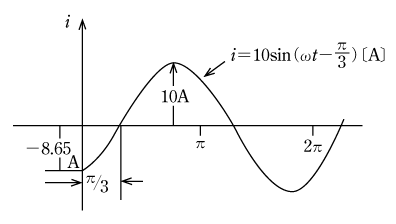
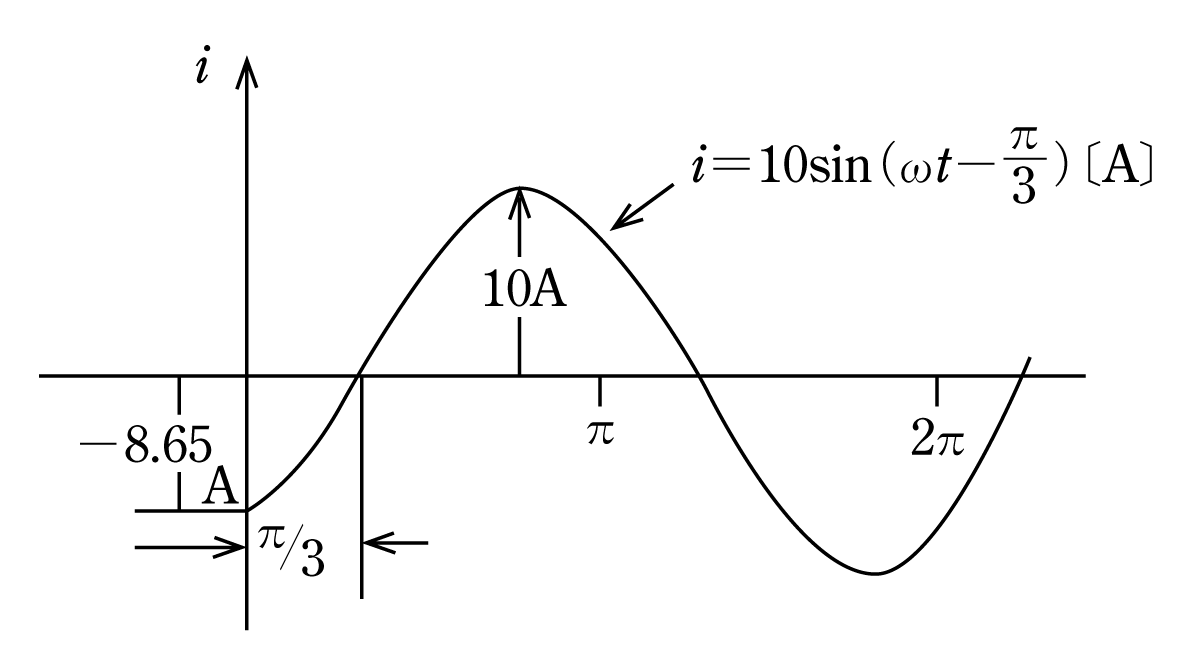
また、i=10sin(ωt-π/3)で、
ωt=0では
![]()
![]()
ωt=π/3ではi=10sin0=0
となるからiの波形のグラフは第8図のようになる。
eの位相角はθ1=π/6、iの位相角はθ2=-π/3であるから、位相差はθ1―θ2=π/6-(-π/3)=π/2〔rad〕となる。
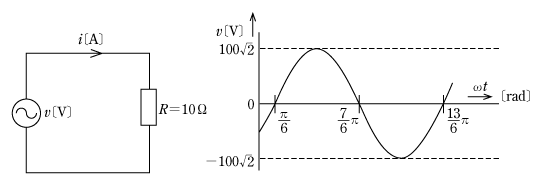
(例題2)図の回路において、右のような正弦波交流電圧v〔V〕を抵抗R=10Ωに加えたとき、流れる電流の瞬時値i〔A〕を表す式として正しいのは次のうちどれか。ただし、電源の周波数を50Hzとする。
(1)10sin(50π t-π/6) (2)10sin(50π t+π/6)
(3)10sin100π t (4)
![]()
![]()
(5)
![]()
![]()
〔解答〕与えられた電圧波形の瞬時値の式は、
である。ただし、ωt=2πft=100π t
瞬時値iは抵抗負荷Rであるから、電圧vと同相で次のように表される。
〔答〕(5)
(例題3)
![]()
![]() 〔V〕と
〔V〕と
![]()
![]() 〔A〕で表される電圧と電流の位相差を時間で表すと、正しいのは次のうちどれか
〔A〕で表される電圧と電流の位相差を時間で表すと、正しいのは次のうちどれか
(1)1/50 (2)1/100 (3)1/100π (4)1/240 (5)1/1,200
〔解答〕
Eをsinで表せば、位相をπ/2進める必要があるので、位相差θは、
この位相差を時間で表すには、ωt=θを満足するtを求めればよい。
ω=100πであるから、
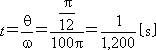
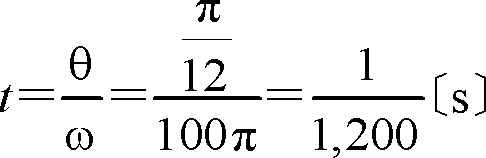
〔答〕(5)
(例題4)ある回路に、
![]()
![]() 〔A〕の電流が流れている。この電流の瞬時値が、時刻t=0〔s〕以降に初めて4〔A〕となるのは、時刻t=t1〔s〕である。t1の値として正しいのは、次のうちどれか。
〔A〕の電流が流れている。この電流の瞬時値が、時刻t=0〔s〕以降に初めて4〔A〕となるのは、時刻t=t1〔s〕である。t1の値として正しいのは、次のうちどれか。
(1)1/480 (2)1/360 (3)1/240 (4)1/160 (5)1/120
〔解答〕時刻t1での瞬時値i=4〔A〕を電流の式に代入すると、
変形すると
![]()
![]()
sinの値が
![]()
![]() になるときは、角度がπ/4〔rad〕のときなので、
になるときは、角度がπ/4〔rad〕のときなので、
π /4=120π t1
〔答〕(1)