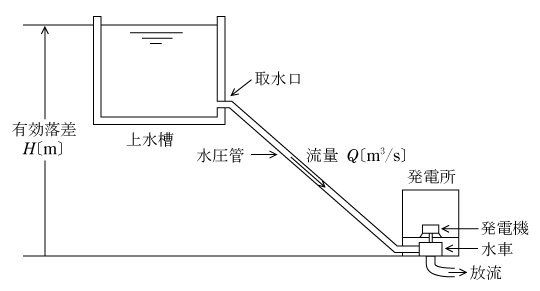
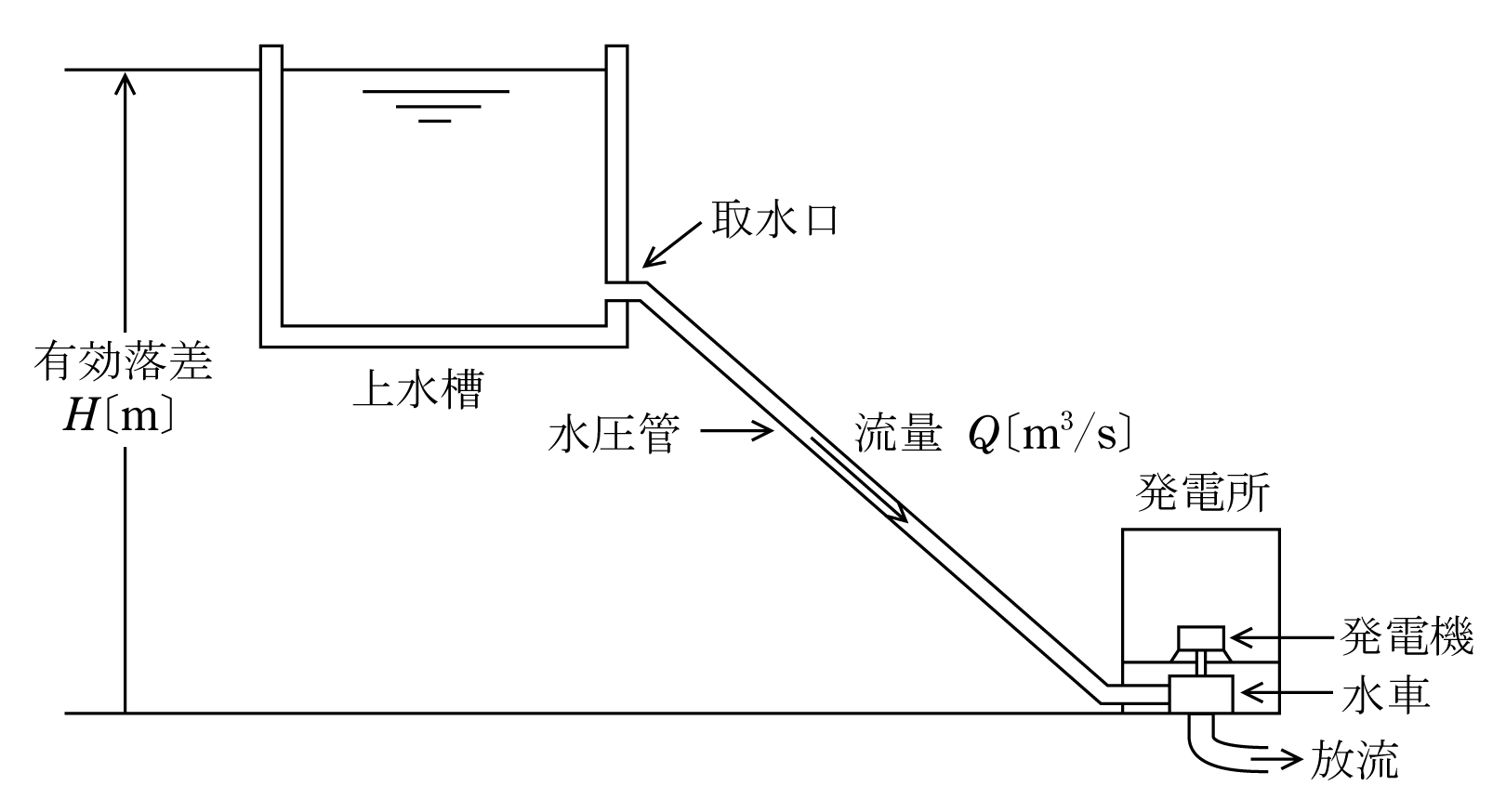
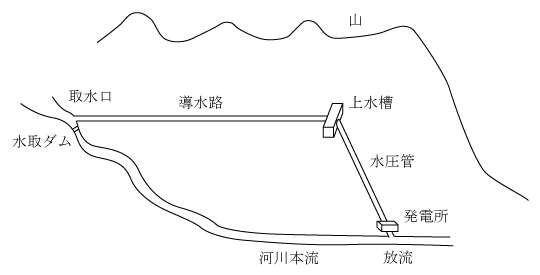
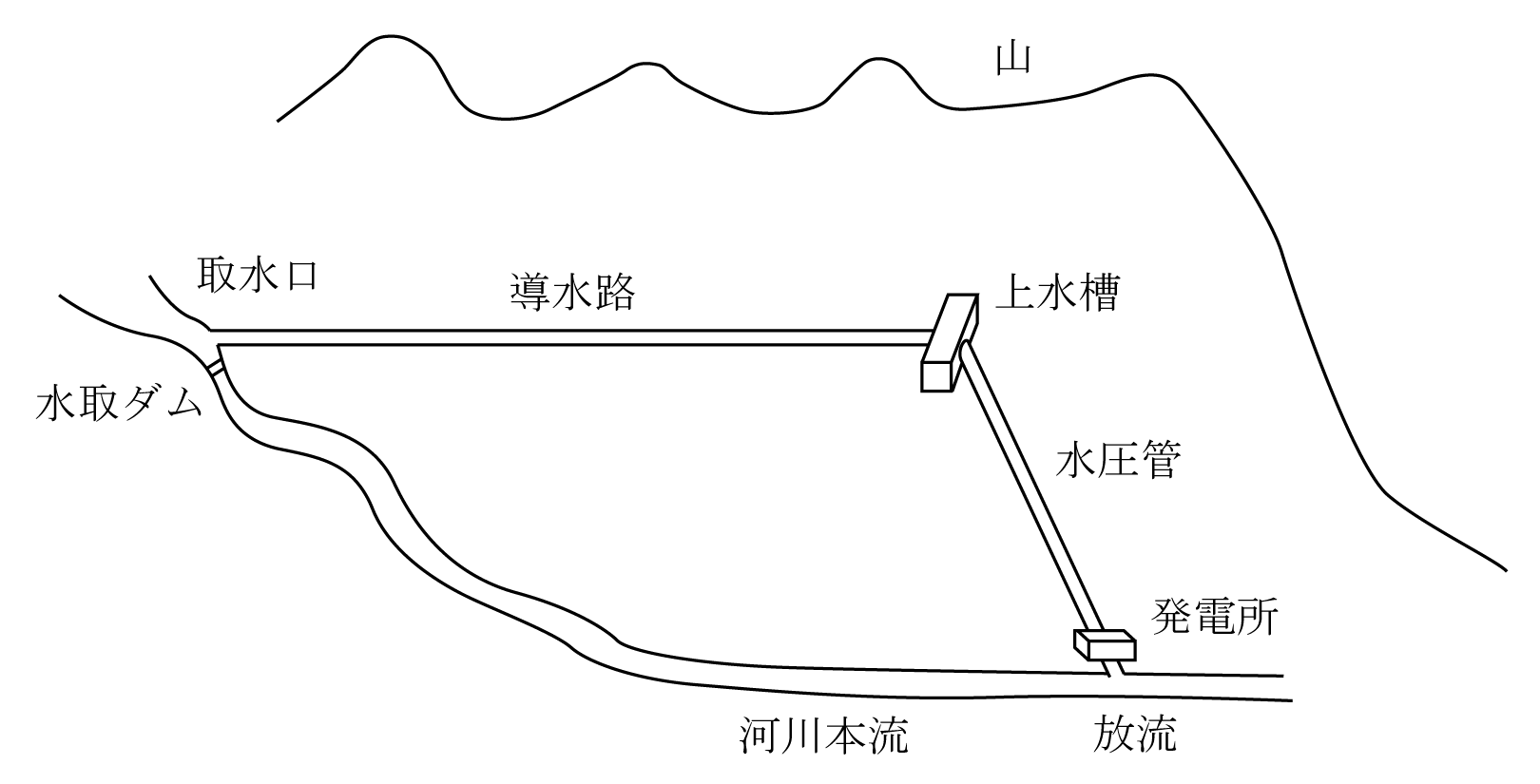
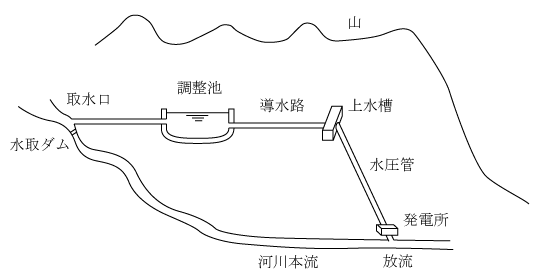
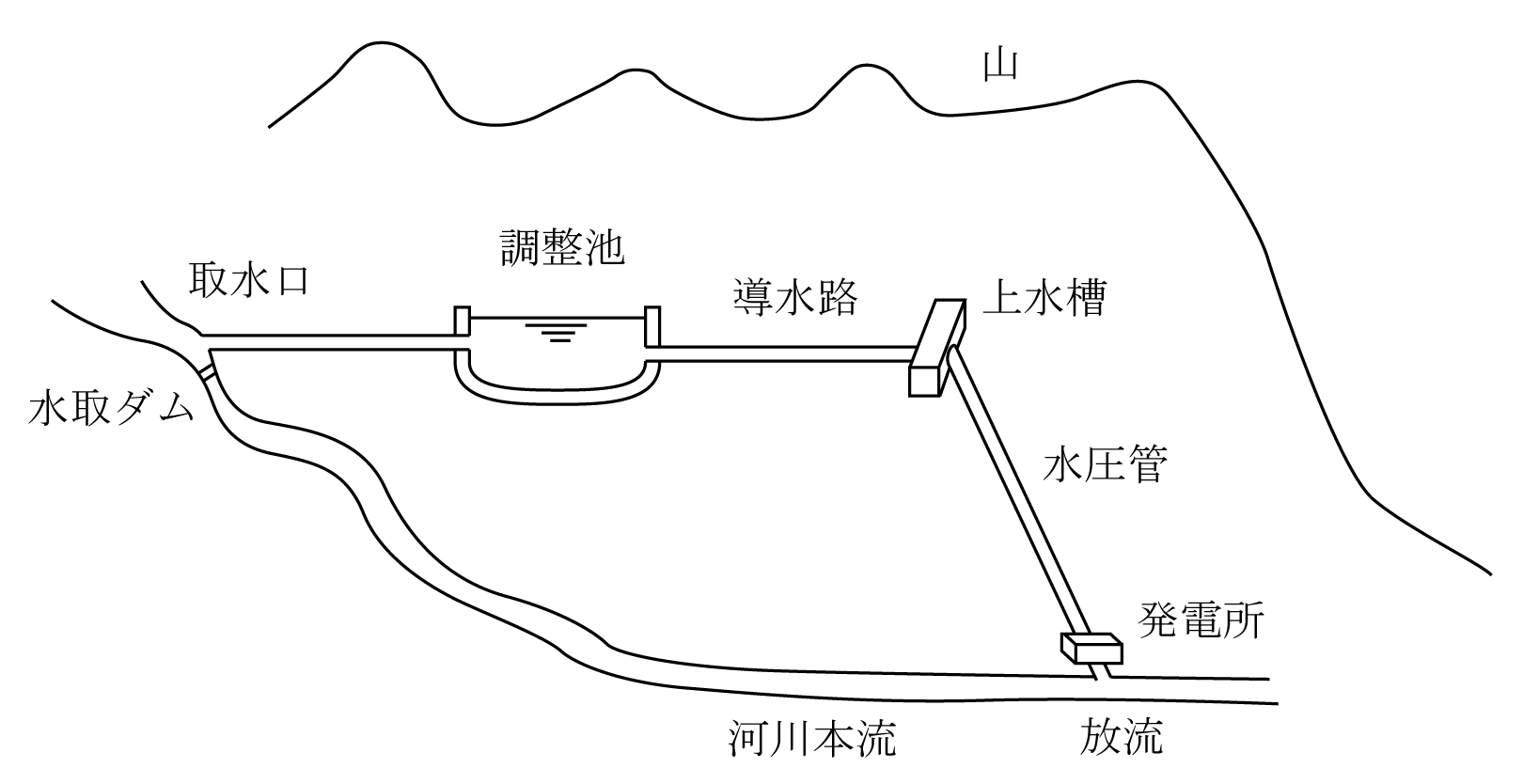
水力発電所での水の流れは、第1図のように河川の上流の山間部で取水した水を上水槽から水圧管を通して発電所の水車に投入して回転させ、河川の下流に放流される。このとき水車と直結している同期発電機で発電する。

　上水槽の水面と水車の間の有効落差:H〔m〕、水の流量Q〔m³/s〕=1,000Q〔kg/s〕、重力加速度g〔m/s²〕=9.8とすると、1秒間の位置のエネルギーH_p〔J/s〕=〔W〕は(1)式となり、

　　　　H_p =1,000QgH=9.8QH×1,000〔W〕= 9.8QH〔kW〕(1)

水車、発電機の効率をη_t、η_gとすると、水力発電所の出力P〔kW〕は(2)式となる。

　　　　P=9.8QHη_tη_g〔kW〕(2)

　次に発電使用水量をV〔m³〕とすると、発電電力量W〔kWh〕は(3)式となる。

　　　　W=9.8(V/3,600) Hη_tη_g〔kWh〕(3)

■第1図　水力発電所の基本イメージ■

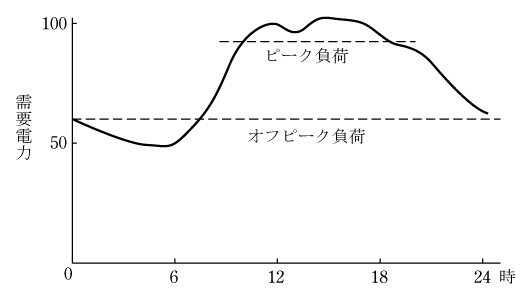
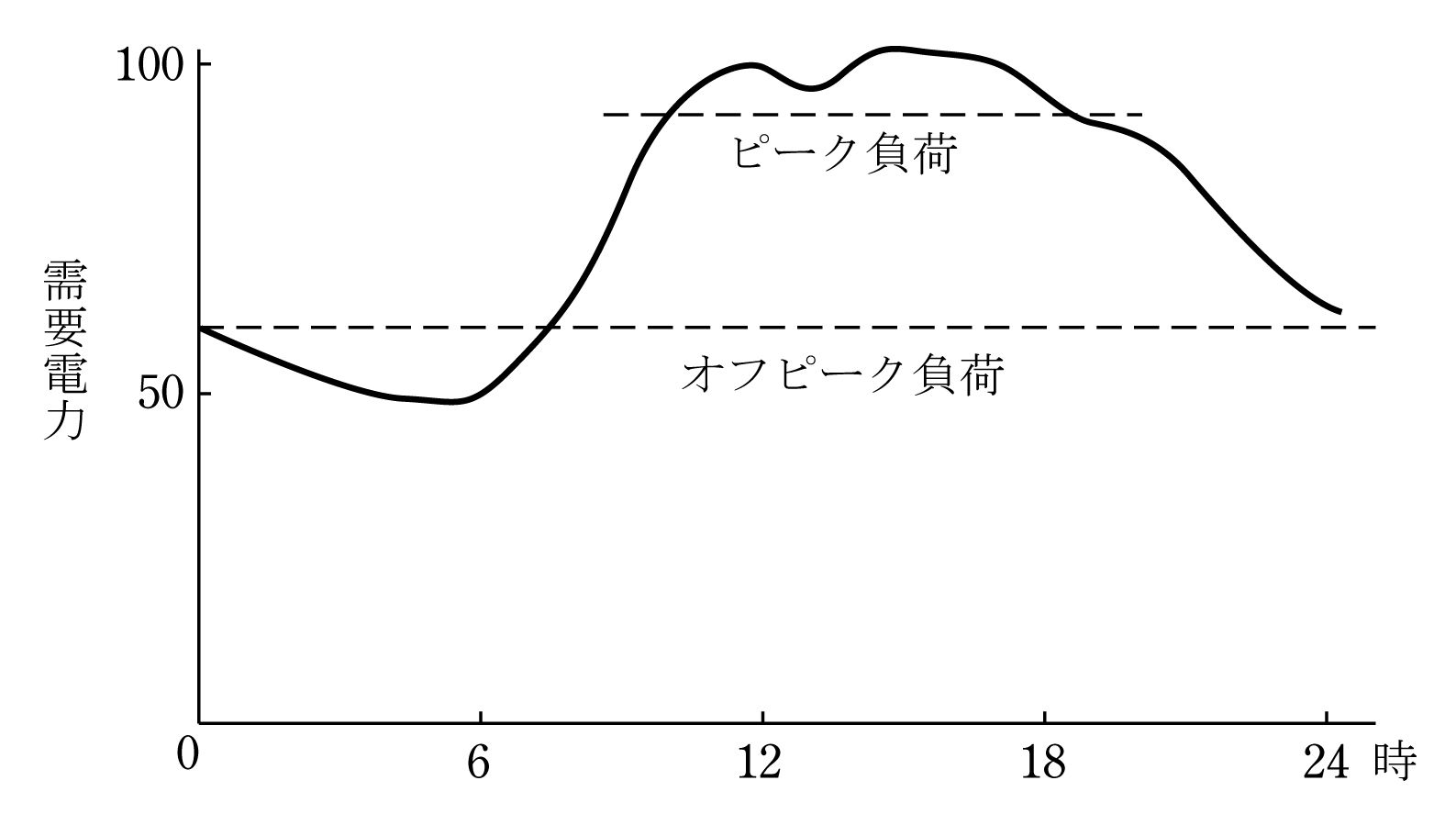
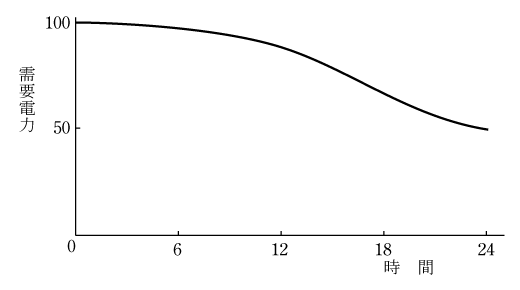
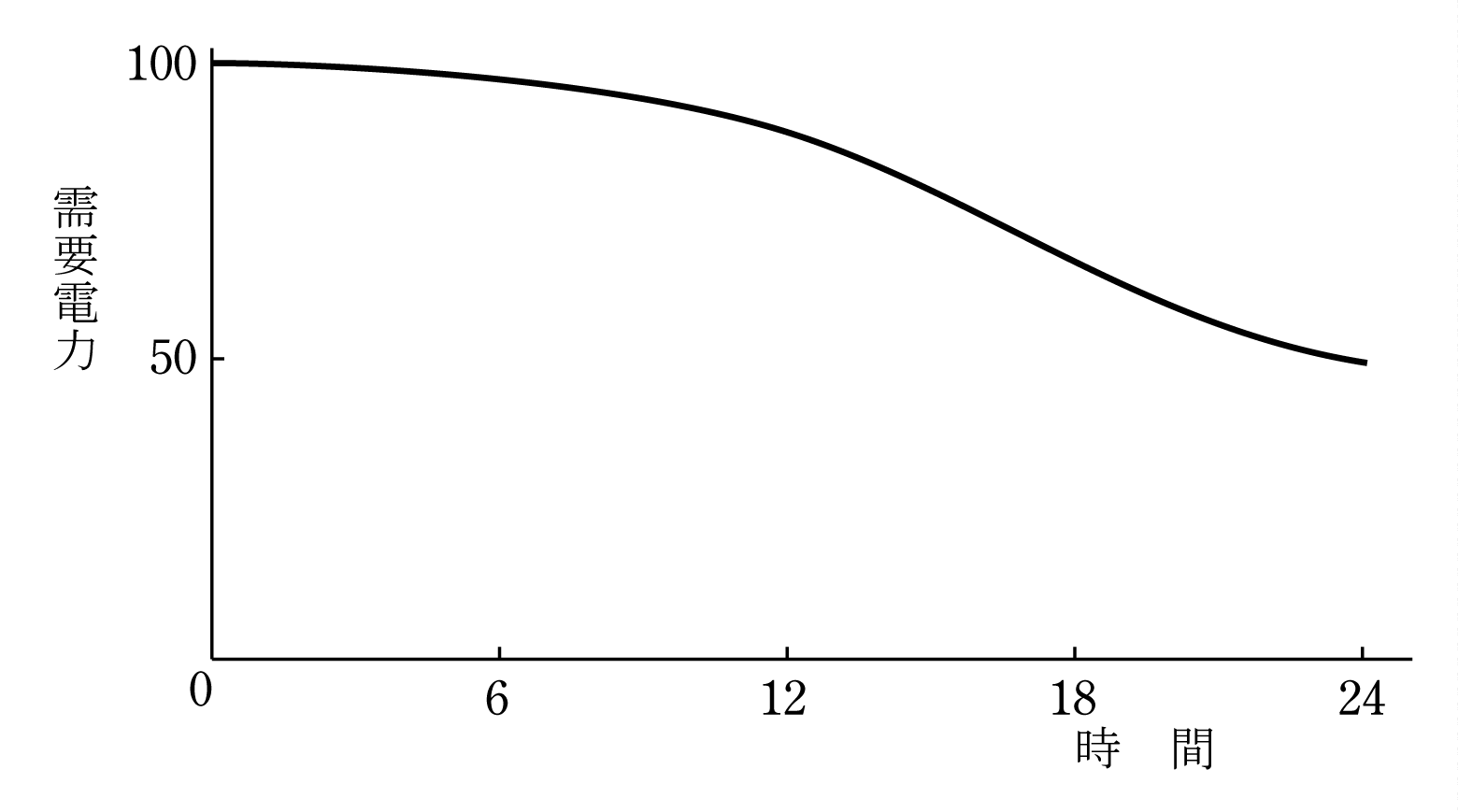
　1日の全需要を総合した電気の使われ方は第2図のように横軸を0時から24時、縦軸を電力として電力の変化を表すと、夜間は少なく早朝からしだいに増加し、仕事が始まる9時ごろから急増し最大値に達した後、仕事が終了する夕方から減少し深夜になると最小になる。これを日負荷曲線という。電気がたくさん使われる時間帯をピーク、深夜などの少ない時間帯をオフピークという。これに対応するには1日一定の発電だけではなく、ピーク時に大量の発電が必要になるので、水力発電所には3章のような発電方式がある。

　負荷持続曲線は第3図のように縦軸は電力、横軸は24時間として日負荷曲線をもとにして、電力の大きい順に並べて作成される。

■第2図　日負荷曲線■

■第3図　日負荷持続曲線■

　水力発電所ではH、ηはほぼ一定である。出力P〔kW〕の調整は流量Q〔m³/s〕を調整して行われる。このことから流量Qの利用方法を基本に以下の4発電方式がある。

（1）自流(流込み)式

　概要を第4図に示す。図のように河川の上流に取水口を設けて水を取水し、ほぼ水平(1/1000～1/1500勾配)な導水路を通して上水槽に移動させる。河川の下流側に発電所を設けて有効落差を確保し、両者間に水圧管を設置する。これによって第1図と同様に流量Q〔m³/s〕と有効落差H〔m〕の水力発電所となる。

　この方式は取水した河川水量をそのまま利用することになるので水量の調整はできず、1日24時間河川流量に合わせた発電になる。これを自流(流込み)式という。

■第4図　自流(流込み)式■

（2）調整池式

　概要を第5図に示す。図のように取水口と上水槽の導水路の中間に調整池と呼ばれる貯水池を設ける。これによって自流式とは異なり、調整池を利用して水を蓄え、ピーク時など必要な時間に必要な発電するなど河川流量と異なる発電ができる。

■第5図　調整池式■

（3）ダム式

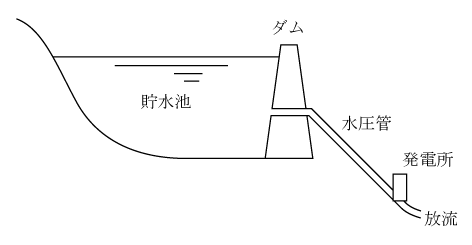
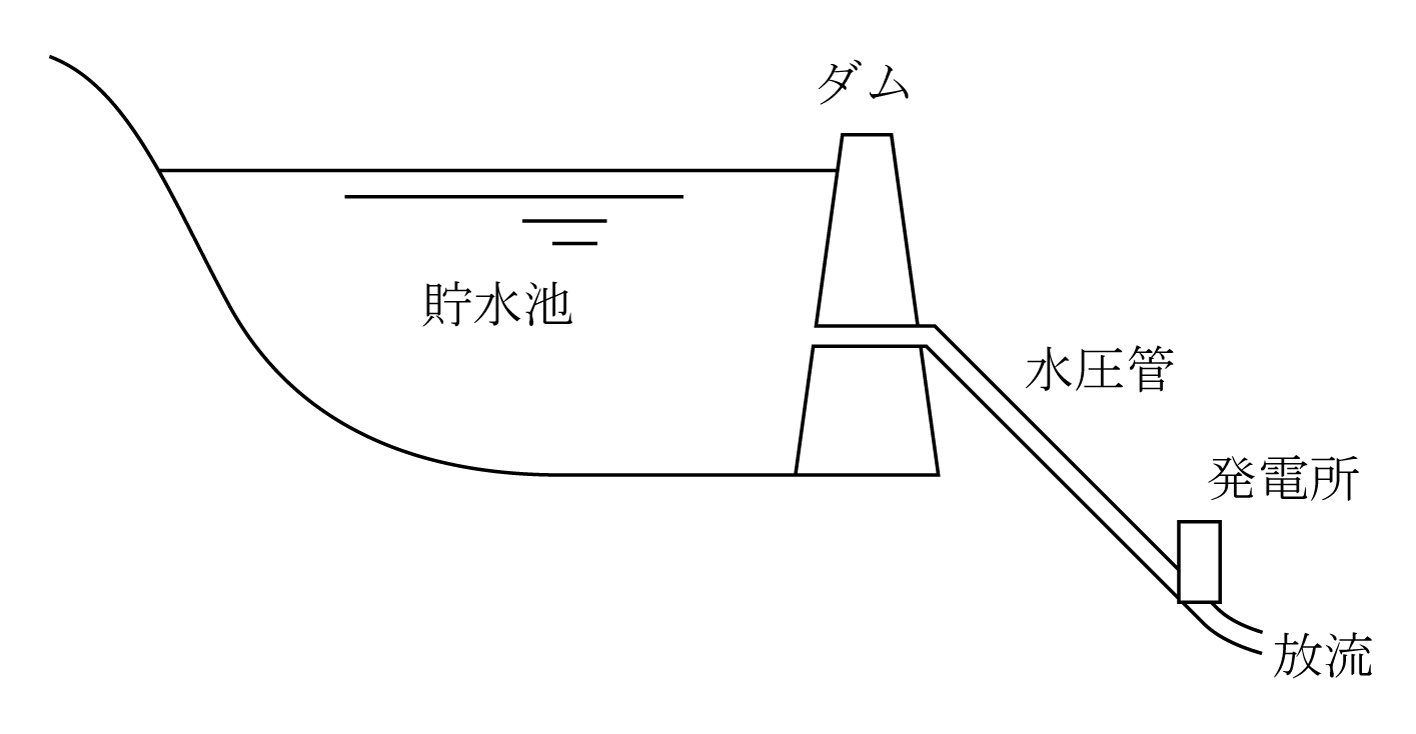
　概要を第6図に示す。図のように河川の上流側に大きなダムを設け、大量の水を貯水する。ダムの直下に発電所を設ける。ダムと発電所間に水圧管を設置し、第1図と同様の発電所とする。使用後の水量は下流の河川に放水する。大量の水を貯水できるので100万kW前後の大容量発電所で主にピーク時に発電する。

■第6図　ダム式■

（4）揚水式

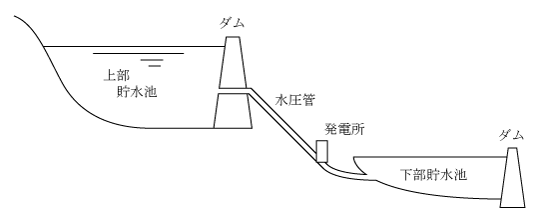
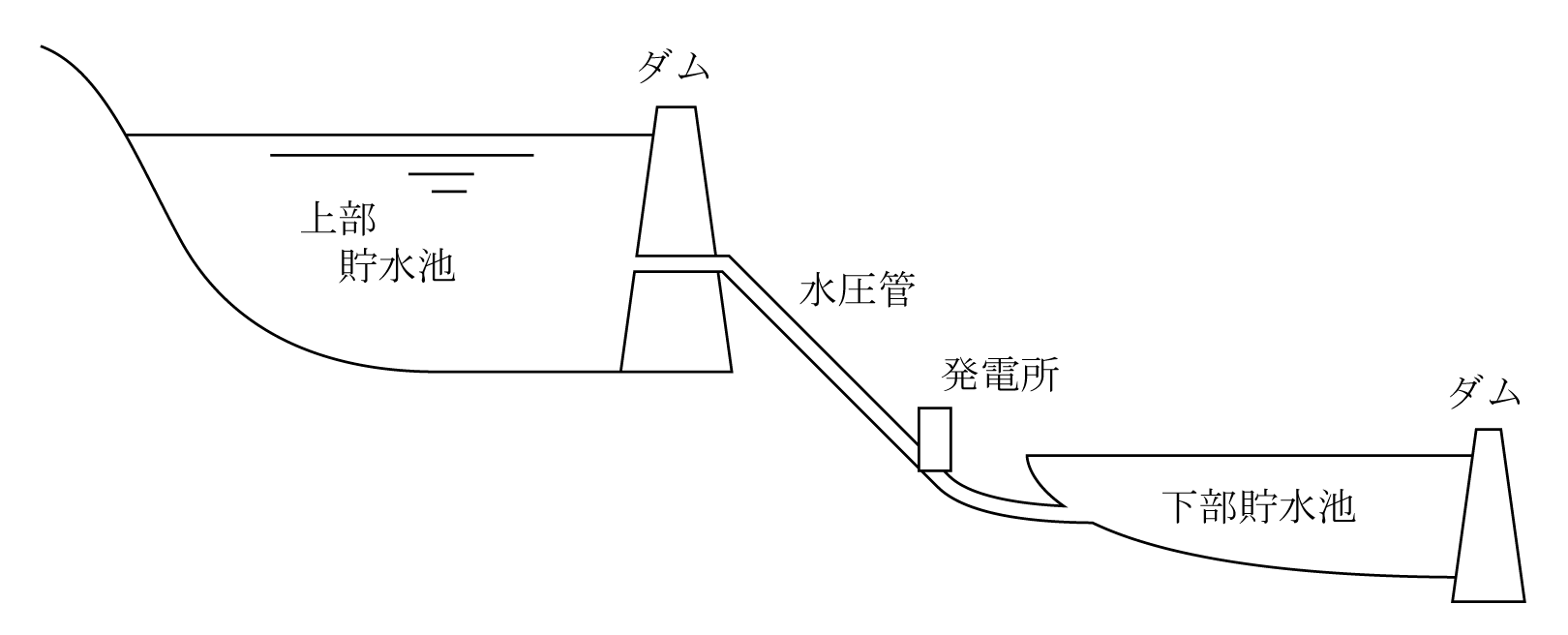
　概要を第7図に示す。図のように河川の上流側にダムを設け、上部貯水池として大量の水を貯水し、ダムの直近に発電所を設け、その下流側に下部貯水池として更にダムを設ける。発電はダム式と同様であるが、使用後の水量は放流せず下流の下部貯水池に貯水し、夜間電力を使ってポンプで上部貯水池に揚水する。これによって河川流量以上の発電が可能となる。なお、発電所の水車と発電機はポンプと電動機に切替えできる機能をもっている。

　2章で述べたようにオフピーク時は発電に余裕があり、ピーク時に比べて電力料金が安価なので、揚水式発電所ではオフピーク時の夜間に揚水し、ピーク時に発電する。ピーク時対応するための大容量発電所である。

■第7図　揚水式■

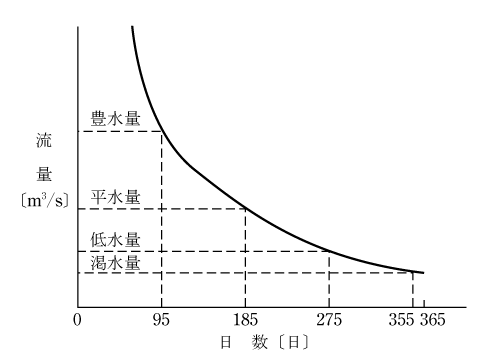
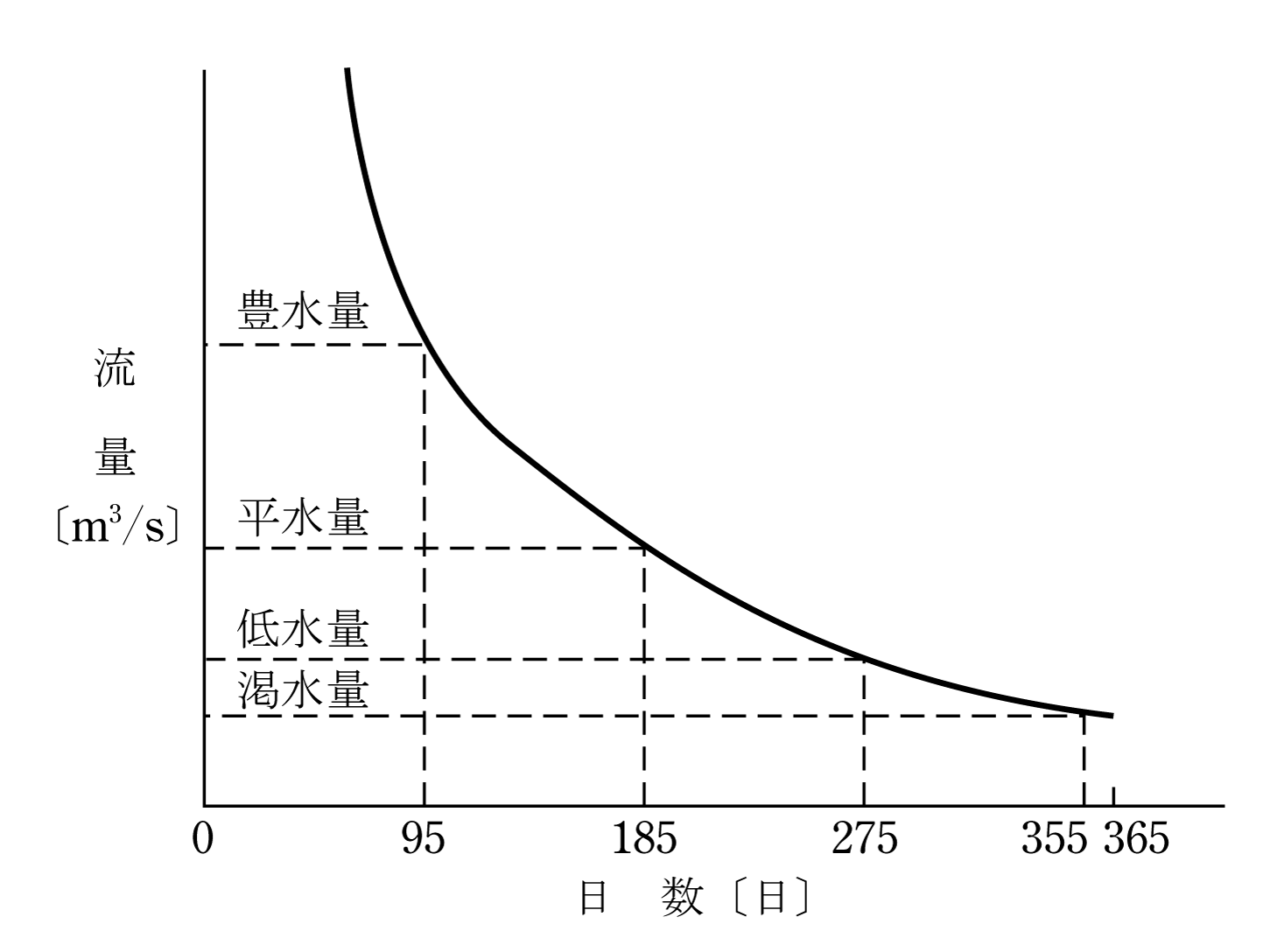
　流況曲線は第8図のように年間の1日当たりの平均流量Q〔m³/s〕を大きな順に365日表示するものである。自流式では最大使用水量を超えたものは取水口から直接放流される。調整池式では貯水池の大きさで満杯になるまで貯水し、それ以上は放流する。ダム式、揚水式では大量の貯水ができるので、台風等の大雨などを除いて貯水できる。

■第8図　流況曲線■

　過去の問題は以下のとおりで、ポイントを解説する。

（1）日負荷曲線を用いた送受電電力量の計算（H20）

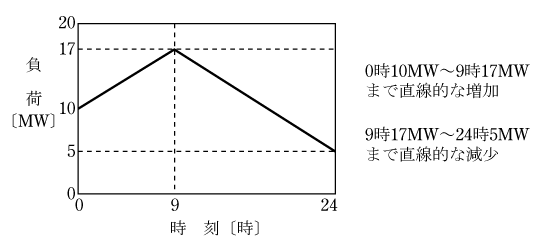
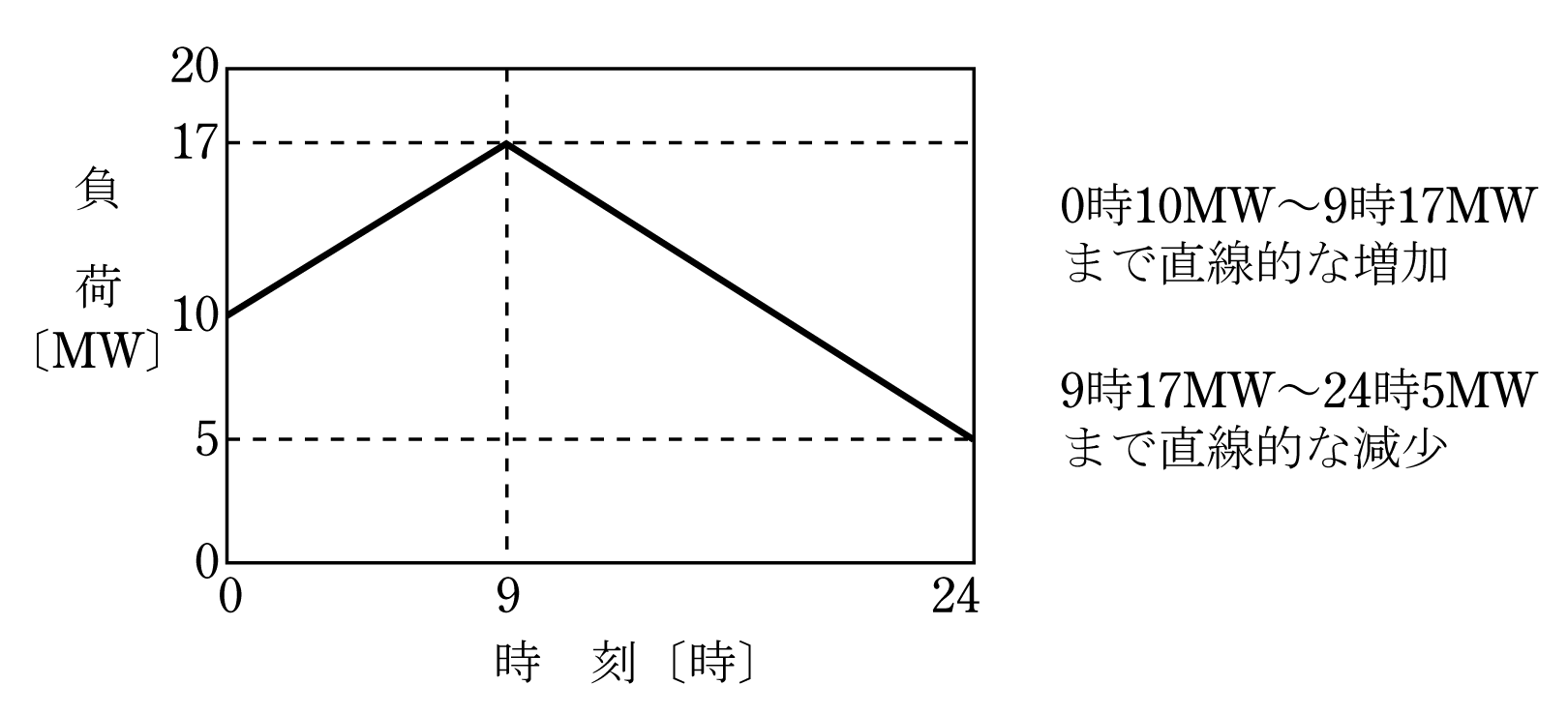
　自家用水力発電所を有し、電力系統(電力会社)と常時系統連系(逆潮流ができるものとする)している工場がある。この工場のある1日の負荷は図のように変化した。

■第9図　問題図(1)■

　この日の水力発電所の出力は10MW一定であった。次の（a）及び（b）に答えよ。

　ただし、水力発電所の所内電力は無視するものとする。

　（a）　この日の電力系統からの受電電力量〔MW･h〕の値として、最も近いのは次のうちどれか。

　　　　(1) 45.4　　　(2) 58.6　　　(3) 62.1　　　(4) 65.6　　　(5) 70.7

　（b）　この日の受電電力量〔MW･h〕(A)に対して送電電力量〔MW･h〕(B)の比率(B/A)として、最も近いものはどれか。

　　　　(1) 0.20　　　(2) 0.22　　　(3) 0.23　　　(4) 0.25　　　(5) 0.28

　（a）の回答

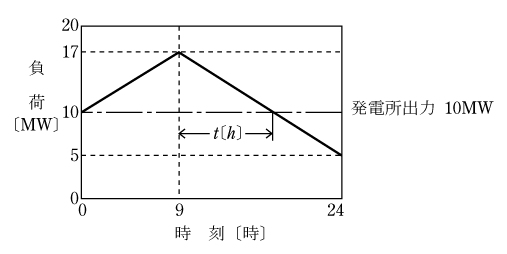
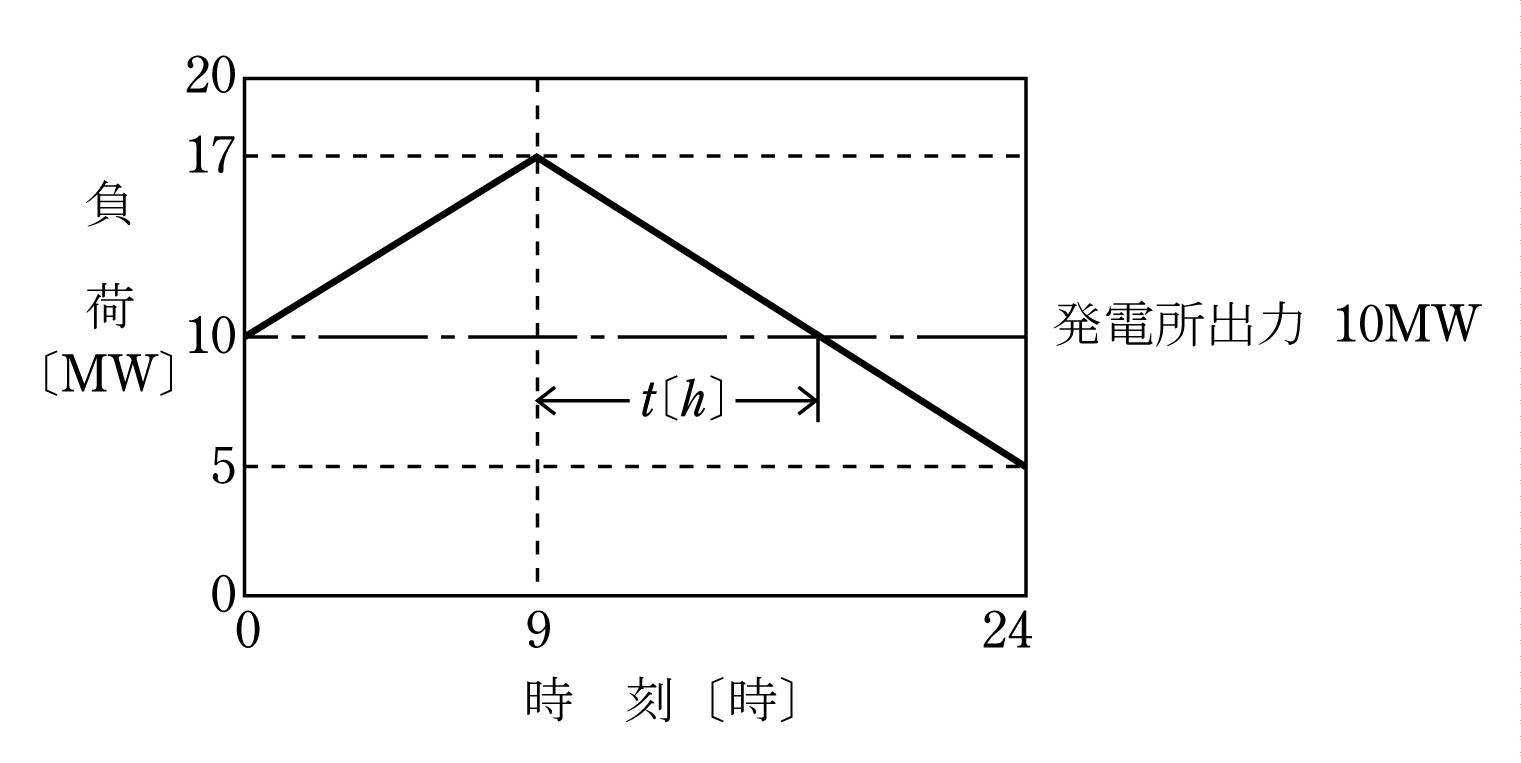
　問題の図面に第10図のように発電所出力10MWの水平線を引き、日負荷曲線が水平線を超えた部分の面積が受電電力量、以下の部分が送電電力量となる。

　図から9時以降負荷が10MWとなるまでの時間t〔h〕は、

　　　　10=17－(17－5)t/(24－9)=17－12t/15=17－4t/5

　　　　t=(17－10)?5/4=8.75h

　受電電力量W_a〔MW・h〕は前述の面積の計算をすると、

　　　　W_a=(17－10)×(9＋8.75)/2=62.125MW・h

　〔答〕　(3)

　（b）の回答

　送電電力量W_b〔MW・h〕は前述のように日負荷曲線が発電所出力以下となる面積なので、

　　　　W_b=(10－5)×(15－8.75)/2=15.625

　　　　送電電力量W_b /受電電力量W_a=15.6/62.1=0.251

　〔答〕　(4)

　問題で示された図面を活用して面積の計算をすることで短時間の回答ができる。

■第10図　回答図(1)■

（2）流込み式発電所の年間流況曲線を用いた計算問題（H15）

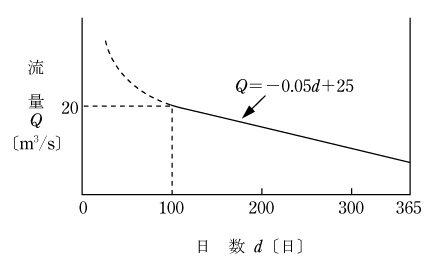
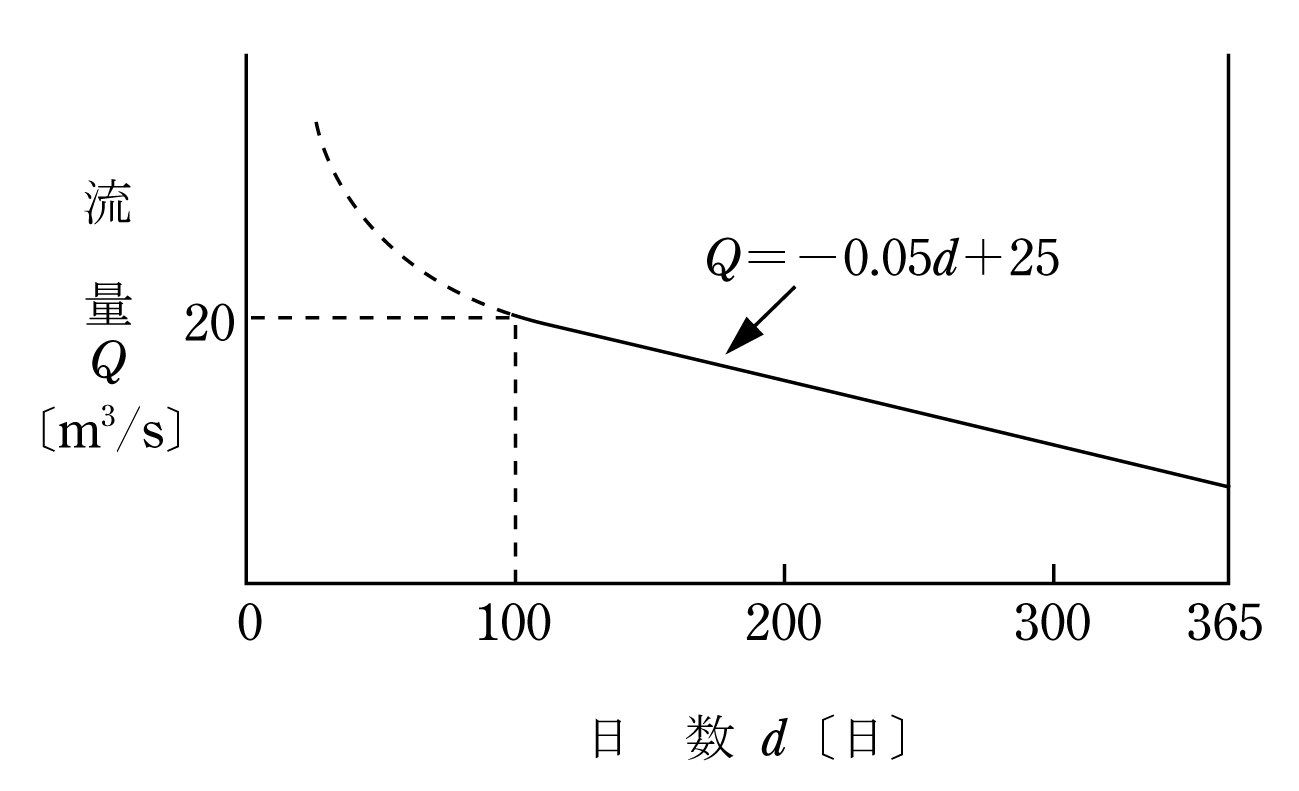
　最大使用水量15〔m³/s〕、有効落差20〔m〕の流込み式水力発電所がある。この発電所が利用している河川の流量Qが図のような年間流況曲線(日数dが100日以上の部分は、Q=－0.05d＋25〔m³/s〕で表される)であるとき、次の（a）及び（b）に答えよ。

　ただし、水車及び発電機の効率はそれぞれ90%及び95%で、流量によって変化しないものとする。

■第11図　問題図(2)■

　（a）　この発電所で年間に溢水が発生する日数の合計として最も近いのは次のうちどれか。

　　ただし、溢水とは河川流量を発電に利用しないで無効に放流することをいう。

　　　　(1) 100　　　(2) 190　　　(3) 200　　　(4) 210　　　(5) 220

　（b）　この発電所の年間可能発電電力量〔GW･h〕の値として、最も近いのは次のうちどれか。

　　　　(1) 19.3　　　(2) 20.3　　　(3) 21.4　　　(4) 22.0　　　(5) 22.5

　（a）の回答

　溢水は河川流量Qが最大使用水量15m³/sを超えた場合に発生するので、

　　　　Q=－0.05d＋25=15m³/sから、

　〔答〕　(3)

　（b）の回答

　・365日目の流量Q´=－0.05d＋25=－0.05×365＋25=6.75m³/s

　・200日まではQ=15m³/s一定なので全流量Q ₁は、

　　　　Q₁=15×24時間?200日=72,000m³/s･時間

　・200～365日間は流量曲線が傾斜した直線で200日の流量Q=15m³/s、365日の流量

　Q´=6.75m³/sから、全流量Q ₂は台形面積で求められるので、

　・合計流量Q₃=Q₁＋Q₂=72,000＋43,065=115,065m³/s･時間

　・年間可能発電電力量W〔GW･h〕は、

　　　　W=9.8×合計流量Q₃×有効落差h×10^-6×個々の効率

　　　　　=9.8×115,065×20×10^-6×0.9×0.95=19.28GW･h

　〔答〕　(1)

（3）調整池式での必要なときの発電電力の計算（H17）

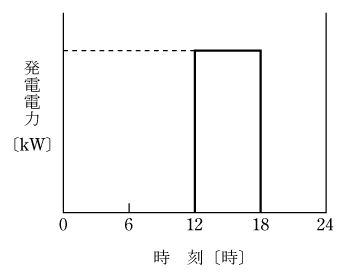
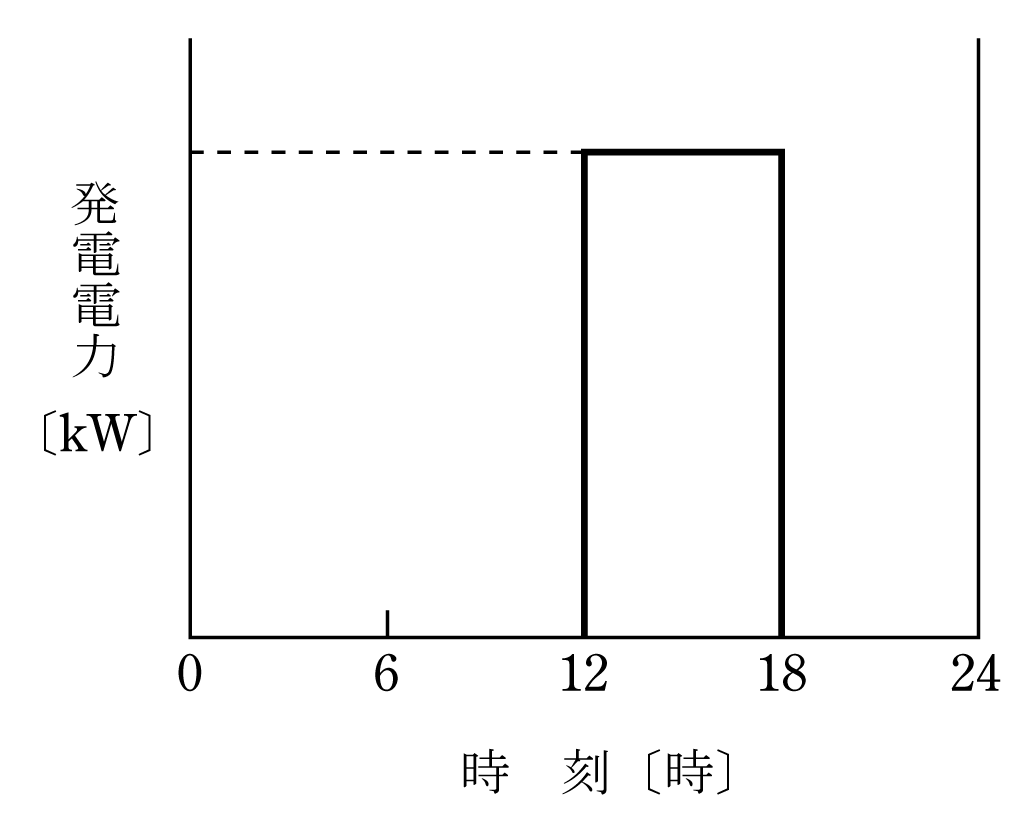
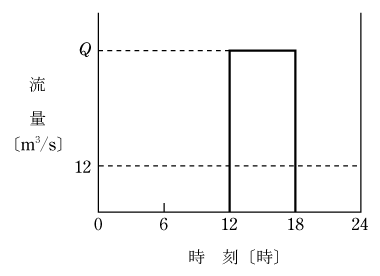
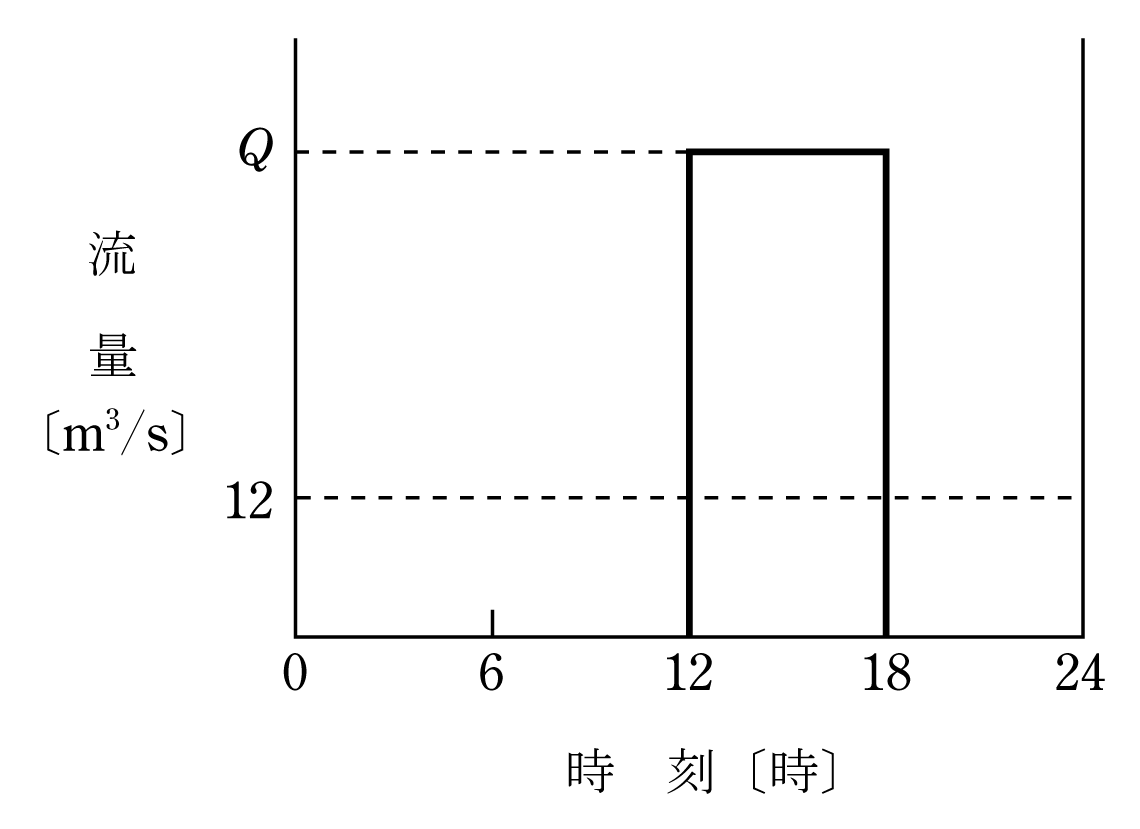
　有効落差80mの調整池式水力発電所がある。河川の流量が12m³/s一定で、第12図のように1日のうち18時間は発電せずに全流量を貯水し、6時間だけ自流分に加え貯水分を全量消費して発電を行うものとするとき，次の（a）及び（b）に答えよ。

　ただし，水車及び発電機の総合効率は85％、運転中の有効落差は一定とし、溢水はないものとする。

■第12図　問題図(3)■

　（a）　1日当たりの総流入量〔m³〕の値として、最も近いのは次のうちどれか。

　　　(1) 288×10³　　　　(2) 780×10³　　　(3) 860×10³

　　　(4) 1,040×10³　　　(5) 1,730×10³

　（b）　発電電力〔kW〕の値として，最も近いのは次のうちどれか。

　　　(1) 20,000　　　(2) 27,000　　　(3) 28,000　　　(4) 32,000　　　(5) 37,000

　（a）の回答

　1日当たりの総流入量Q_m〔m³〕は第13図のように河川の流量が12m³/s、24時間の面積の計算をする。ただし、1時間=3,600sを考慮して、

　　　　Q_m=12×24×3,600=1,036,800m³

　〔答〕　(4)

　（b）の回答

　第13図のように総流入量Q _mを調整池に貯水して6時間ですべて使用するので総流入量=使用水量から、1s当たりの流量Q〔m³/s〕は、

　　　　　12×3,600×24=Q×3,600×6　から、

　発電電力P〔kW〕は、

　　　　　P=9.8QHη=9.8×48×80×0.85=31,987kW

　〔答〕　(4)

■第13図　回答図（3）■

　この問題も示された図面を活用して面積の計算をすることで短時間の回答ができる。