〜終わり〜
■ぜひアンケートにご協力下さい■


比例式は、二つの変数の関係を表す一次式の最も簡単な場合であり、一方の変数がもう一方の変数にある倍率を乗じた値になる式である。オームの法則により電気回路の電圧と電流は比例する、コンデンサに蓄えられる電荷は電圧に比例する、回転機械ではトルクと機械的出力は比例するなど、電験の問題を解く場合にはさまざまな比例式が登場する。また、指数関数は、大きな数から小さな数までを簡潔に表し、積商の計算するのに便利である。電気回路や物理の定理や法則の式は、積や商であらわす式が多く、計算の方法に慣れ、使いこなせるようになっておくことが重要である。ここでは、比例式や指数の考え方、実際の問題の解答での応用のされ方、効率よく使うための方法を学ぶ。
比例式としてなじみの深いのは、導体の抵抗Rは長さlに比例し、断面積Sに反比例するという式
![]()
![]() であるが、この式でlが2倍になると抵抗も2倍になる。つまり長さの増す割合と同じ割合で抵抗も増加する。これが比例である。また、断面積が2倍になると抵抗は1/2になる。つまり断面積の倍数の反対(逆にした数)になるので、反比例と呼んでいる。
であるが、この式でlが2倍になると抵抗も2倍になる。つまり長さの増す割合と同じ割合で抵抗も増加する。これが比例である。また、断面積が2倍になると抵抗は1/2になる。つまり断面積の倍数の反対(逆にした数)になるので、反比例と呼んでいる。
ところで、抵抗率ρはなぜ比例に関係しないのかと考えるかもしれないが、これは数学上では比例定数と呼ばれるもので、もともと比例というのは割合だけを考えているので、実際の数値は考慮しなくてよいのである。この理由をもう少していねいに説明しよう。
いま、同じ断面積で、長さだけがl1の導体とl2の導体があるとする。長さl1のほうの抵抗をR1、l2のほうの抵抗をR2とすれば、
![]()
![]() 、
、
![]()
![]() となるが、
となるが、
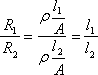
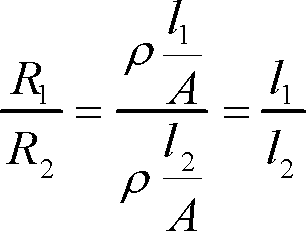
となって抵抗率ρは消えてしまう。つまり長いほうが抵抗も大きく、その割合は長さの割合になる。
比例という言葉の場合には、実際の数字を直接には問題にしていない。
しかし、比例式を用いて導体の抵抗は何Ωあるかということになると、銅線であるか、アルミ線であるか、鉄線であるかによって、長さや断面積が同一であっても、導体のオーム数はみな異なるはずである。そこで、それぞれの材料のl=1、A=1のときの値が分かれば、これをもとにして、一般に長さがlで、断面積がAの材料の抵抗が分かるはずである。つまり、
これが抵抗率であり、比例定数というものの存在する意義がある。比例式は形の上では分数式であるが、割合の概念という面で応用する場合、大切な内容を持っていることを事例をもとに示してみよう。
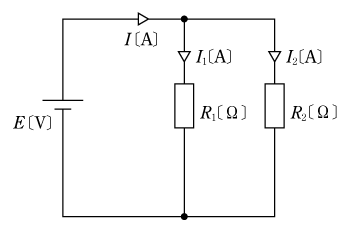
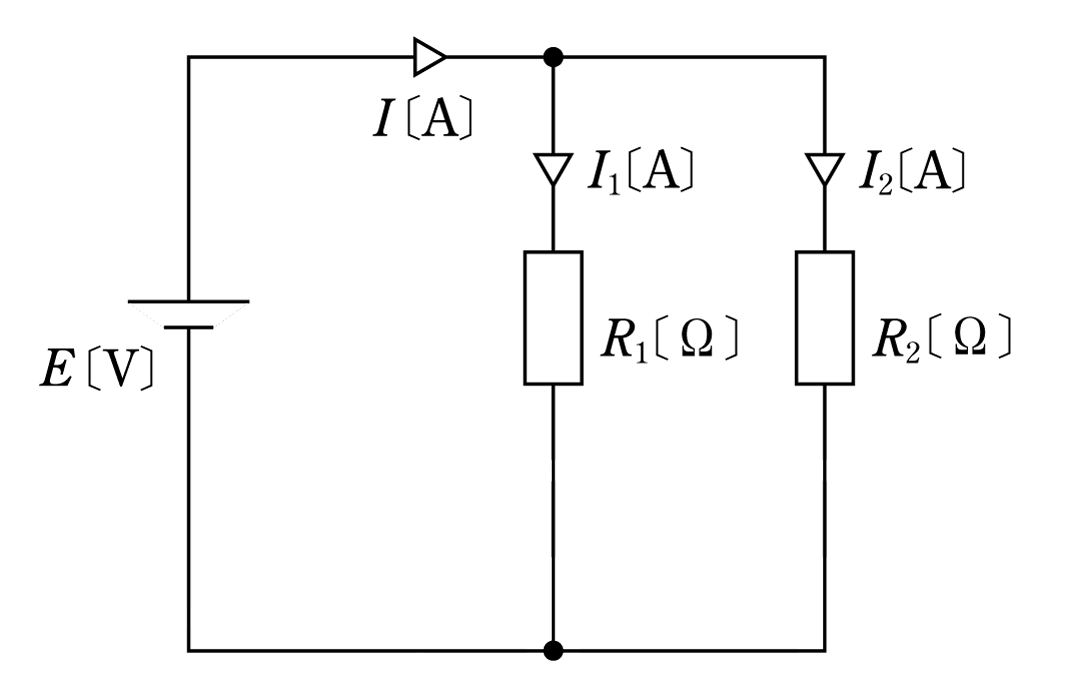
〔例題1〕 第1図に示す回路の全電流
![]()
![]() が分岐回路にどのような割合で分流するかを、比例式の考え方を用いて示せ。
が分岐回路にどのような割合で分流するかを、比例式の考え方を用いて示せ。
第1図の分岐回路の電流は、
![]()
![]() 、
、
![]()
![]() であるから、
であるから、
これを比例式という立場でみると電流の比例関係と、抵抗の比例関係が逆になっている。これは反比例の関係である。つまりI1がI2より大きくなるためには、R2のほうがR1より大きくなければならない。このことをもっとはっきりさせるために式を書き換えてみる。
比例計算で面白いのは「合比の理」といわれるもので、
![]()
![]() の比例式の両辺に1を加えて計算を進めてみると、
の比例式の両辺に1を加えて計算を進めてみると、
![]()
![]() 通分して
通分して
![]()
![]()
ここで第1図を見るとI1+I2=Iであるから、
また、電流
![]()
![]() については、
については、
![]()
![]() から
から
![]()
![]() であるから同様に、
であるから同様に、
![]()
![]() から
から
![]()
![]()
よって、
この(1)、(2)式は、全電流Iが分岐回路にどのような割合で分流するかを示す公式としてよく用いられる。
(参考) 合比の理に対して除比の理がある。これは例えばa/b=c/dの比例式があるとき、両辺から1を引いて、
![]()
![]() ゆえに
ゆえに
![]()
![]()
とすることである。
累乗(るいじょう)とは、同じ数または同じ文字を次々に掛けた積をいう。累は重ねるという意味である。指数とは累乗において、その数なり、文字なり、式なりを何個掛け合わせたかを示す数のことで、指数はその数を、数字または文字の右肩に小さく書いて示す。式の場合は括弧でくくって括弧の右肩に書く。
〔指数法則〕
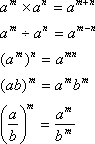
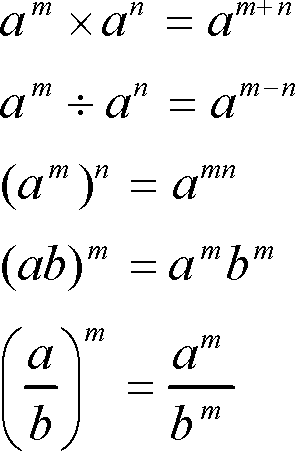
これらの指数法則が成り立つことは
![]()
![]() と
と
![]()
![]() とに実際の数字を入れてみればすぐ分かる。
とに実際の数字を入れてみればすぐ分かる。
(参考) 例えば、いまm=4、n=2として、
もしm=2、n=4とすると、
となるが、このときも公式をそのまま用いると、
つまりマイナスの指数は逆数(分子を1とする分数)を表すものと約束すればよいことになる。しかし、一つ約束が必要である。その約束とは指数が0になるときである。
![]()
![]() となる。これは
となる。これは
![]()
![]() を
を
![]()
![]() で割った結果を表しているので答が1になるのは当然であるが、公式を用いて計算すると奇妙な指数ゼロという数が現れるので、一応理屈を抜きにして
で割った結果を表しているので答が1になるのは当然であるが、公式を用いて計算すると奇妙な指数ゼロという数が現れるので、一応理屈を抜きにして
![]()
![]() ということで全部の場合を公式化しているのである。
ということで全部の場合を公式化しているのである。
また、指数が分数のときは、指数の分子はn乗、分母はn乗根の意味である。
例えば、
![]()
![]() =
=
![]()
![]() 、
、
![]()
![]() 、
、
![]()
![]() =
=
![]()
![]() =5
=5
〔例題2〕 真空中にある2個の電子の間隔が0.1〔μm〕であるときの両電子の電荷間に働く力をf1〔N〕とし、1個の電子に加わる重力をf2〔N〕とするとき、f1 / f2の値として正しいのは次のうちどれか。ただし、電子の電荷は1.6×10-19 C、電子の質量は9.1×10-31 kg、重力の加速度は9.8m/s2とし、また、
![]()
![]() F/mとする。
F/mとする。
(1)5.13×1013 (2)1.82×1014 (3)2.58×1015
(4)3.47×1016 (5)4.85×1017
〔解答〕 2個の電荷間に働く力f1はクーロン力であるから、電荷e〔C〕とし、電荷間の距離をr〔m〕とすれば、
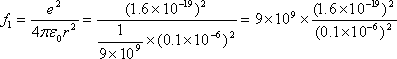
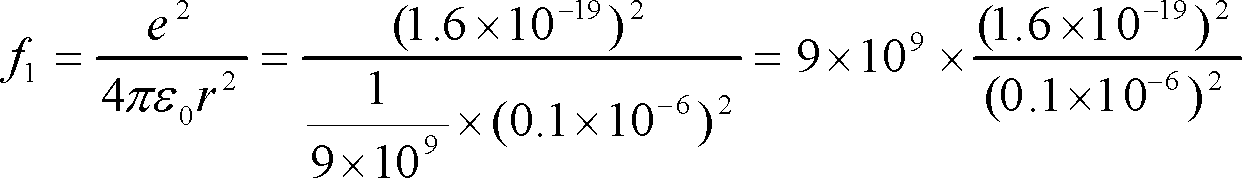
また、1個の電子に加わる重力f2は電子の質量m〔kg〕と重力の加速度g〔m/s2〕の積を求めればよい。
f2=mg=9.1×10-31×9.8=8.918×10-30
したがって、
〔答〕(3)
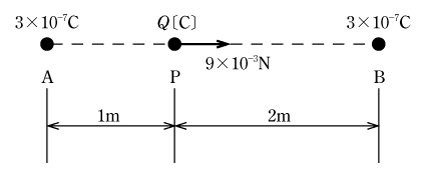
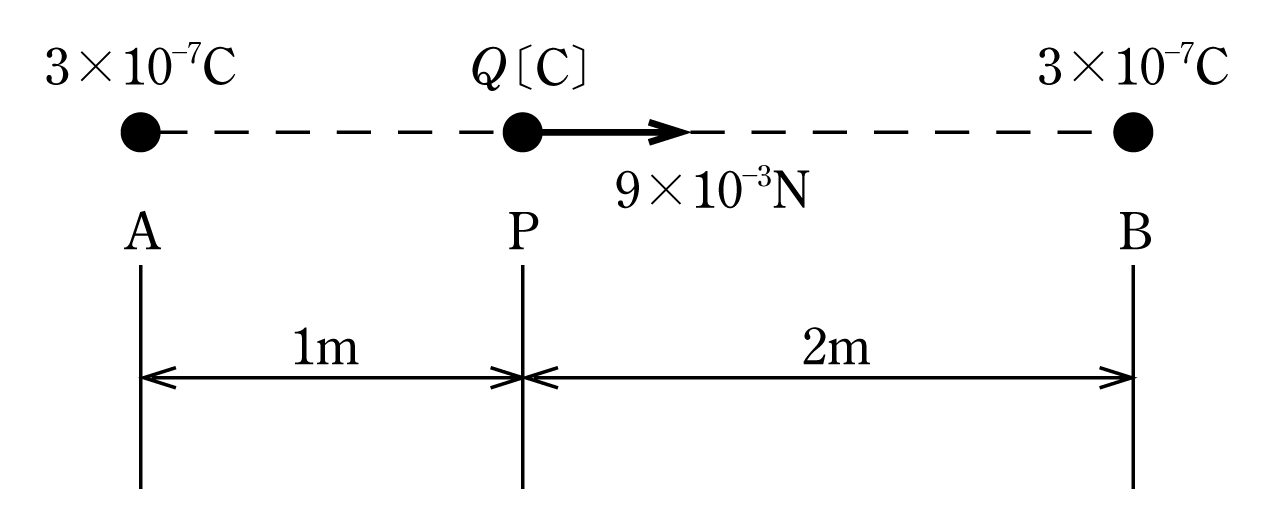
〔例題3〕 第2図のように真空中の3m離れた2点A、Bにそれぞれ3×10-7Cの正の点電荷がある。A点とB点とを結ぶ直線上のA点から1m離れたP点にQ〔C〕の正の点電荷を置いたとき、その点電荷にB点の方向に9×10-3Nの力が働いた。この点電荷Q〔C〕の値として、最も近いのは次のうちどれか。
ただし、真空中の誘電率を
![]()
![]() 〔F/m〕とする。
〔F/m〕とする。
(1)1.2×10-9 (2)1.8×10-8 (3)2.7×10-7
(4)4.4×10-6 (5)7.3×10-5
〔解答〕 点電荷Q〔C〕に働く力は、A点とB点のもつ電荷(3×10-7C)とそれぞれの距離からの合力fである。A点からの距離は1m、B点からの距離は2mであるが、これをそれぞれr1、r2とすると、題意から次の式が成り立つ。
合力fは9×10-3Nであるから、
この式を整理すると、
したがって、
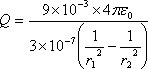
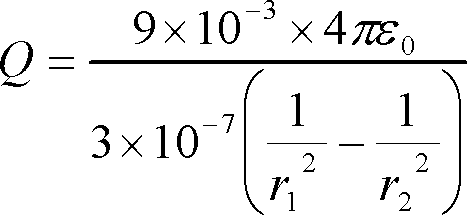
=
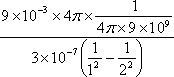
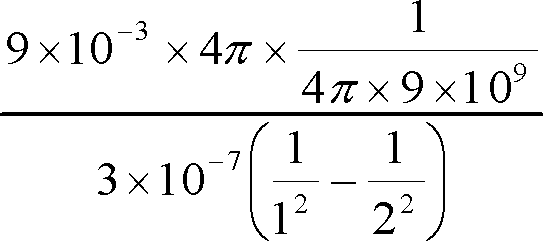
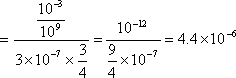
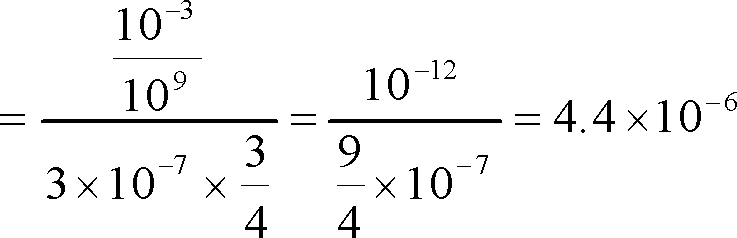
〔答〕(4)
〔例題4〕 水力発電所の水圧管内での単位体積当たりの水が保有している運動エネルギーは、水の密度ρ〔kg/m3〕、水の速度をv〔m/s〕とすると、
![]()
![]() 〔J/m3〕
〔J/m3〕
で表される。この場合ρとv2の単位の積がエネルギーの単位〔J/m3〕になることを示せ。
〔解答〕 単位についての次元を確かめると、次のようになる。
* 1N=1
![]()
![]() である。
である。