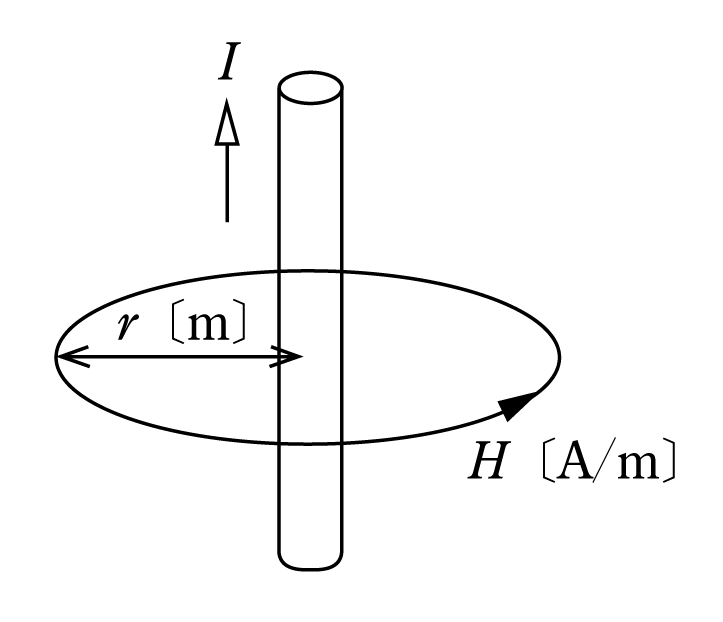〜終わり〜
■ぜひアンケートにご協力下さい■
電流による磁界を計算するための法則としては、ビオ・サバールの法則とアンペア周回路の法則がある。ここでは、各法則の概要と例題による計算手順を解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
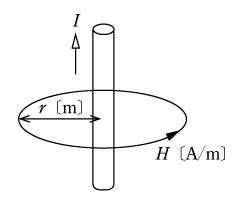
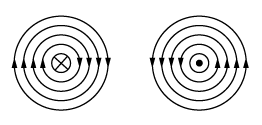
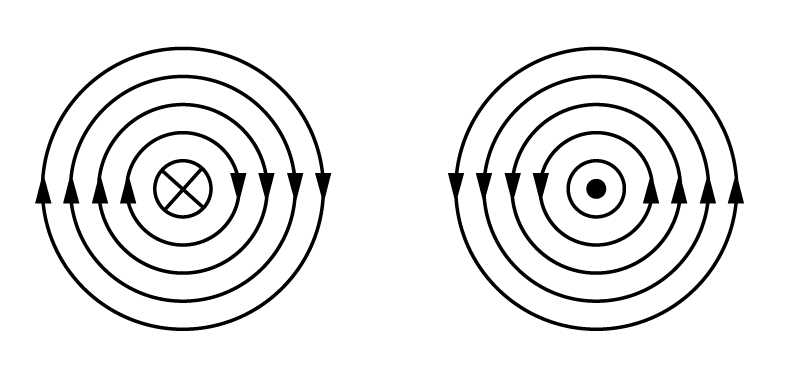
第1図に示すように電線に電流を流すと、その周囲には磁界が発生する。この磁界の方向は、電流が流れる向きと磁界の向きとの関係が、ちょうど右ねじが回転して進む方向と一致する。これをアンペアの右ねじの法則という。第2図は平面的に電流の向きを表したもので、
は手前から奥の方向へ、
は奥から手前の方向へ垂直に電流が流れている方向を示す記号である。
電線に電流を流すとその周囲には第1図に示すように磁界が発生する。この電線から半径r〔m〕離れた円周を考える。この円周上に微小長さΔl1、Δl2、・・・、Δln〔m〕をとり、それぞれの微小長さにおける磁界の強さをΔH1、ΔH2、・・・、ΔHn〔A/m〕とする。このときアンペアの周回積分の法則によって次式が成立する。
〔A〕
〔A〕
半径r〔m〕の円周上では磁界の強さは等しく、これをH〔A/m〕とすれば、
また、
とすれば、
となる。第1図では
〔m〕なので、
∴
となる。
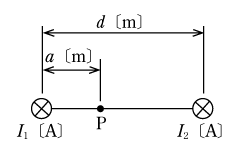
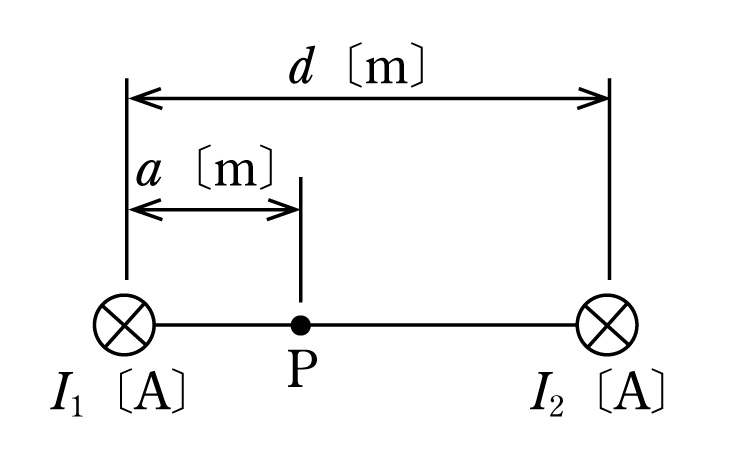
【例題1】 第3図で点Pの磁界の強さがゼロになるときのaの長さ〔m〕はいくらか。
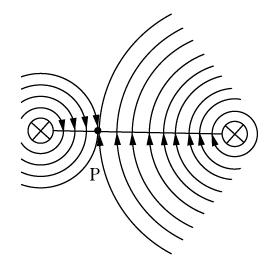
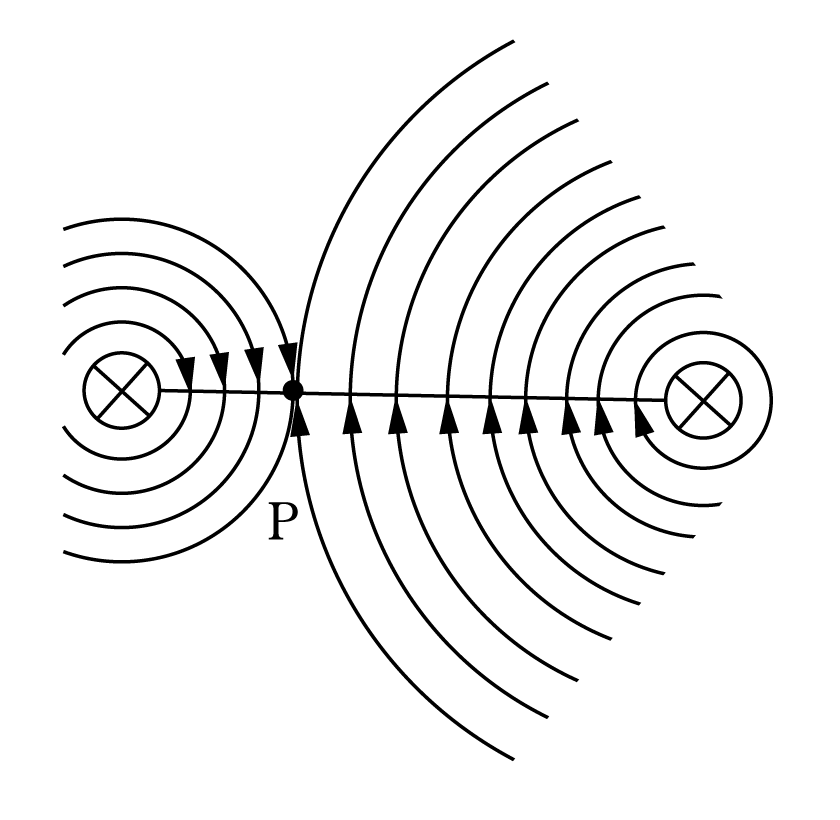
【解説】 電流の向きが同じなので、磁界の方向は第4図に示すようになる。すなわち、点PでI1によって発生する磁界H1とI2によって発生する磁界H2の向きが逆になるので、それぞれの磁界の強さが等しくなったとき、点Pの磁界の強さがゼロになる。よって、
〔A/m〕 ( 1 )
〔A/m〕 ( 1 )
〔A/m〕 ( 2 )
〔A/m〕 ( 2 )
( 1 )式と( 2 )式を等置して整理すれば、
〔m〕
〔m〕
【問題1】 真空中に無限長の直線状電線があり、これに10Aの電流が流れているとき、電線から1m離れた点の磁束密度〔T〕として、正しいのは次のうちどれか。
ただし、真空の透磁率を
〔H/m〕とする。
( 1 ) 1×
( 2 ) 2×
( 3 ) 4×
( 4 ) 2π×
( 5 ) 4π×
【解説】 アンペアの周回積分の法則から、磁界の強さH〔A/m〕は、
〔A/m〕
〔A/m〕
よって、磁束密度Bは、
〔T〕
〔T〕
（答）( 2 )
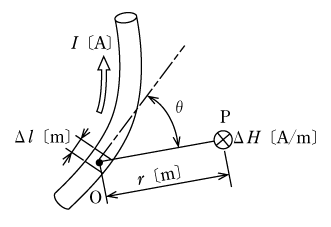
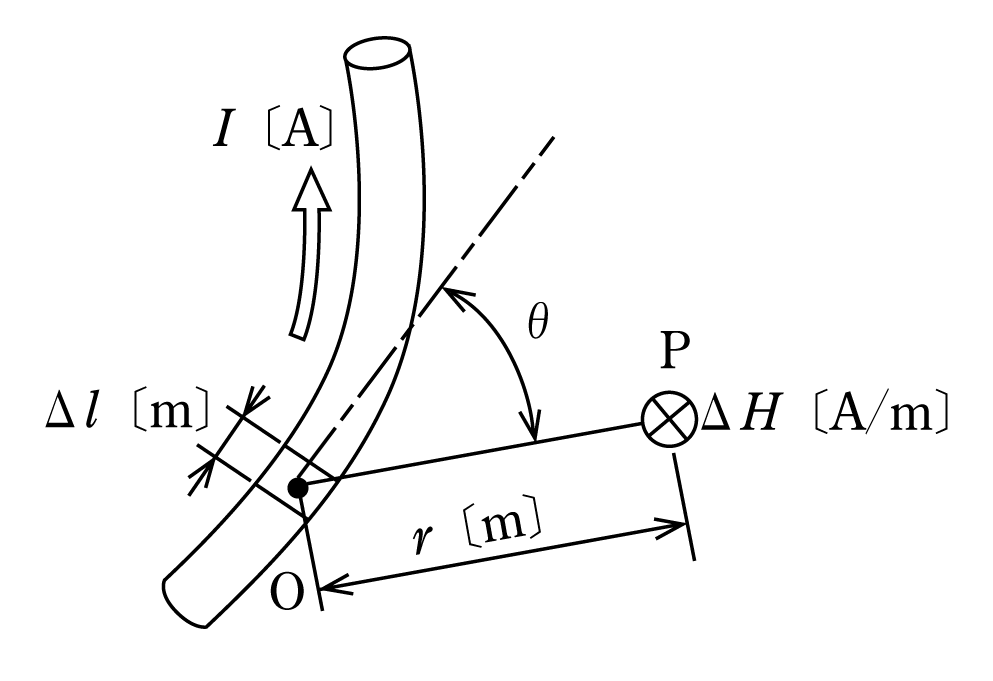
第5図に示すように電線に電流I〔A〕が流れているとする。この電線上の任意の場所に微小長さΔl〔m〕をとり、ここを点Oとする。この点Oからr〔m〕離れた点Pにおける磁界の強さΔH〔A/m〕は、
〔A/m〕 ( 3 )
〔A/m〕 ( 3 )
ただし、θはΔlの接線と線分OPのなす角
で求めることができる。これをビオ・サバールの法則という。
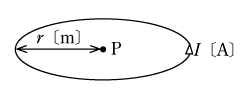
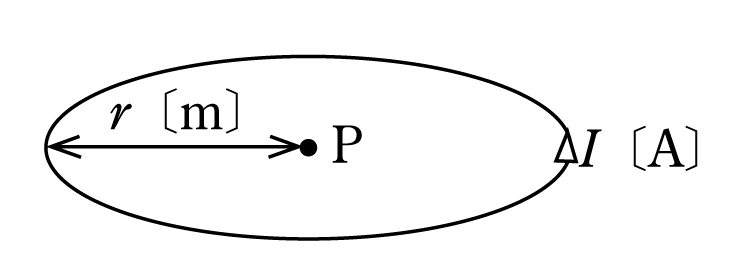
例えば、第6図に示すような円形コイルに電流I〔A〕が流れているものとする。このとき円形コイルの中心Pに生じる磁界の強さを求めてみよう。円形コイル上に微小長さΔl1、
Δl2、・・・、Δln〔m〕をとり、それぞれの微小長さにおける磁界の強さをΔH1、ΔH2、
・・・、ΔHn〔A/m〕とする。それぞれの微小長さと点Pのなす角は常に90°であるから、sinθは常に1となる。よって、ビオ・サバールの法則から中心Pの磁界の強さH〔A/m〕は、
( 4 )
( 4 )
であるから、
であるから、
〔A/m〕 ( 5 )
〔A/m〕 ( 5 )
となる。コイルの巻数がN回であれば、
〔A/m〕 ( 6 )
〔A/m〕 ( 6 )
となる。
【例題2】 半径1〔m〕、巻数1の円形コイルの中心点の磁界の強さが1A/mであるとき、コイルに流れる電流〔A〕はいくらか。
【解説】 ビオ・サバールの法則を用いて解く。( 5 )式を変形して、
A
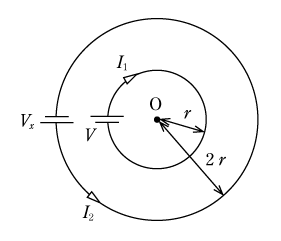
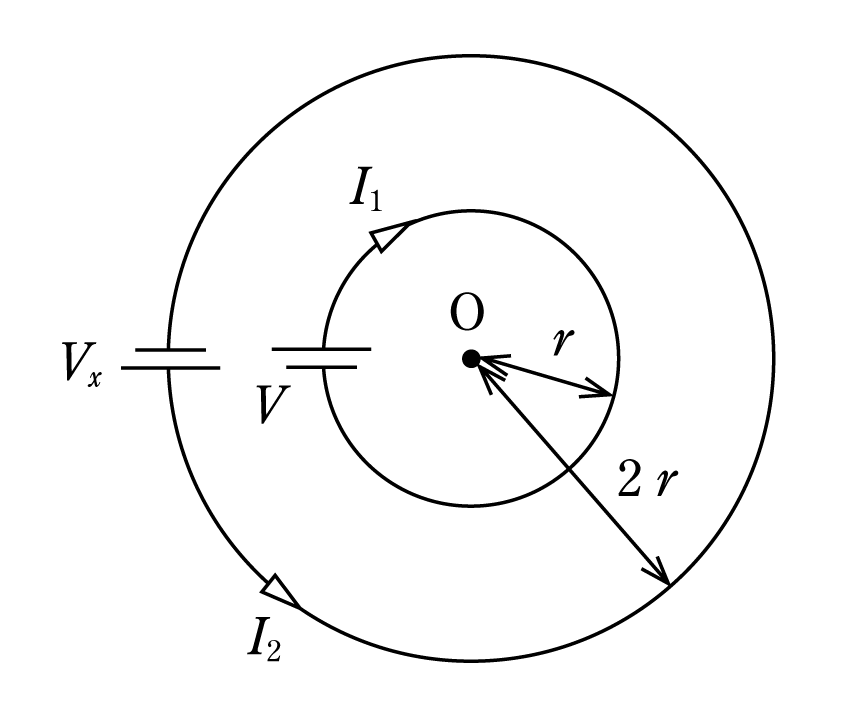
【問題2】 第7図で二つの円形導体は同一材料、同一断面である。中心Oの磁界H0をゼロとするための外側導体の電圧Vx〔V〕を内側導体の電圧V〔V〕で表すとき次のうちで正しいものはどれか。
( 1 ) V ( 2 ) 2V ( 3 ) 4V ( 4 ) 8V ( 5 ) 16V
【解説】 内側の導体の長さをl1、外側導体の長さをl2とすれば、
である。題意から同一材料、同一断面であるので、この抵抗率をρ、断面積をSとする。内側の導体と外側導体の電気抵抗をそれぞれR1〔Ω〕、R2〔Ω〕とすれば、
( 7 )
( 7 )
( 8 )
( 8 )
( 7 )、( 8 )式から、
が得られる。さて、電流I1とI2がそれぞれ中心Oにつくる磁界の強さ、H1、H2は、
( 9 )
( 9 )
( 10 )
( 10 )
中心OでI1によって発生する磁界H1とI2によって発生する磁界H2の向きが逆になるので、それぞれの磁界の強さが等しくなったときに中心Oの磁界の強さがゼロになる。よって、( 9 )式と( 10 )式を等置して整理すると、
∴
（答）( 3 )