〜終わり〜
■ぜひアンケートにご協力下さい■
ベクトル制御の解説書に頻繁に出てくるdq変換と関連技術について易しく解説する。最初に三相二相変換を説明する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
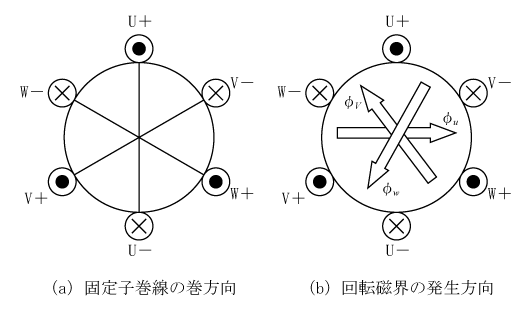
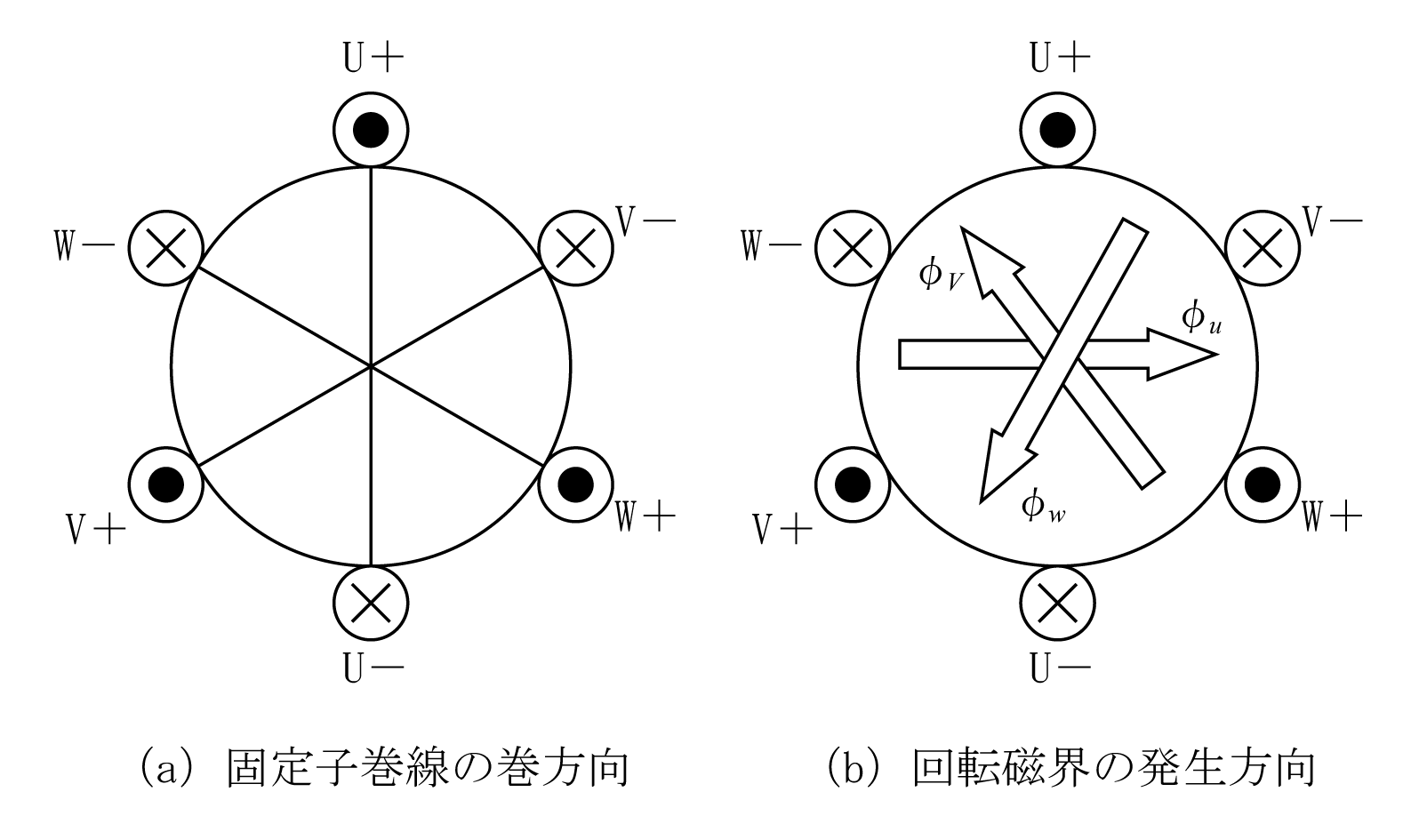
二次回路を含む誘導電動機への展開の準備段階として、まず固定子巻線だけについて考える。三相でドライブされる固定子巻線と回転磁界を第1図のようにモデル化する。
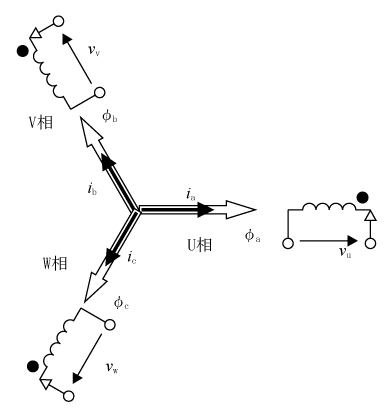
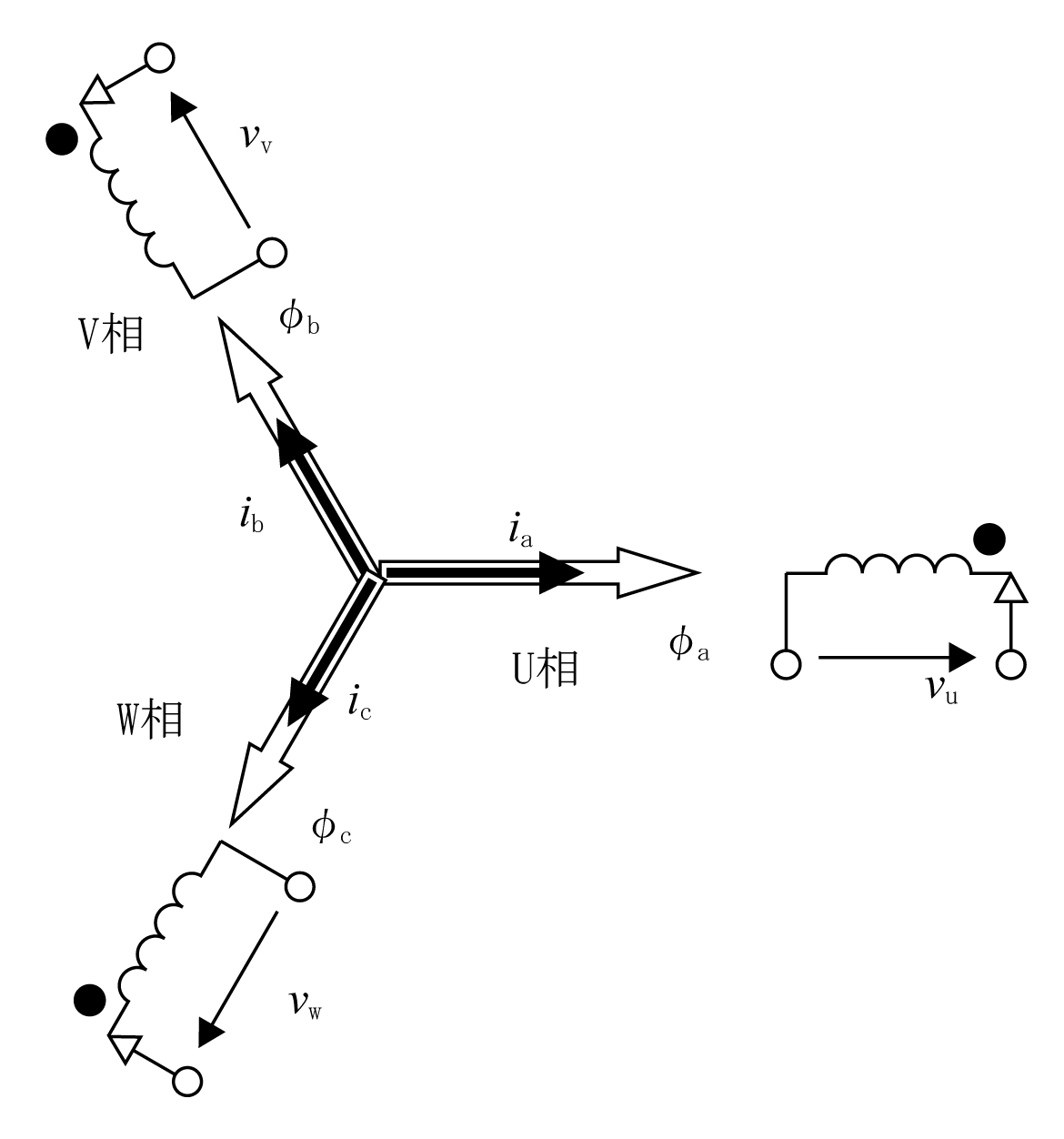
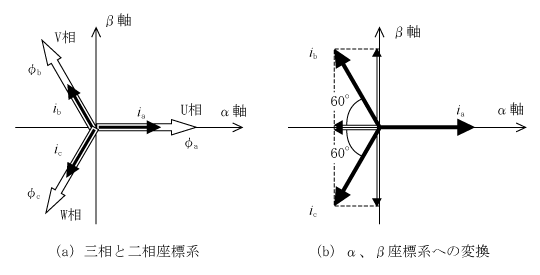
第1図（a）で示すコイルにU、V、W相の三相電圧を加え、電流を流すと第1図（b）φu、φv、φwのように回転磁界が発生する。しかし、この図では以後の展開に不都合なので、第2図のように表現する。すなわち、U、V、W相に各コイルをスター（Y）状に配置し、磁束φの方向を各相の方向に合わせる。また、電流ベクトルの方向を磁束の方向としてia、ib、icで記述する。
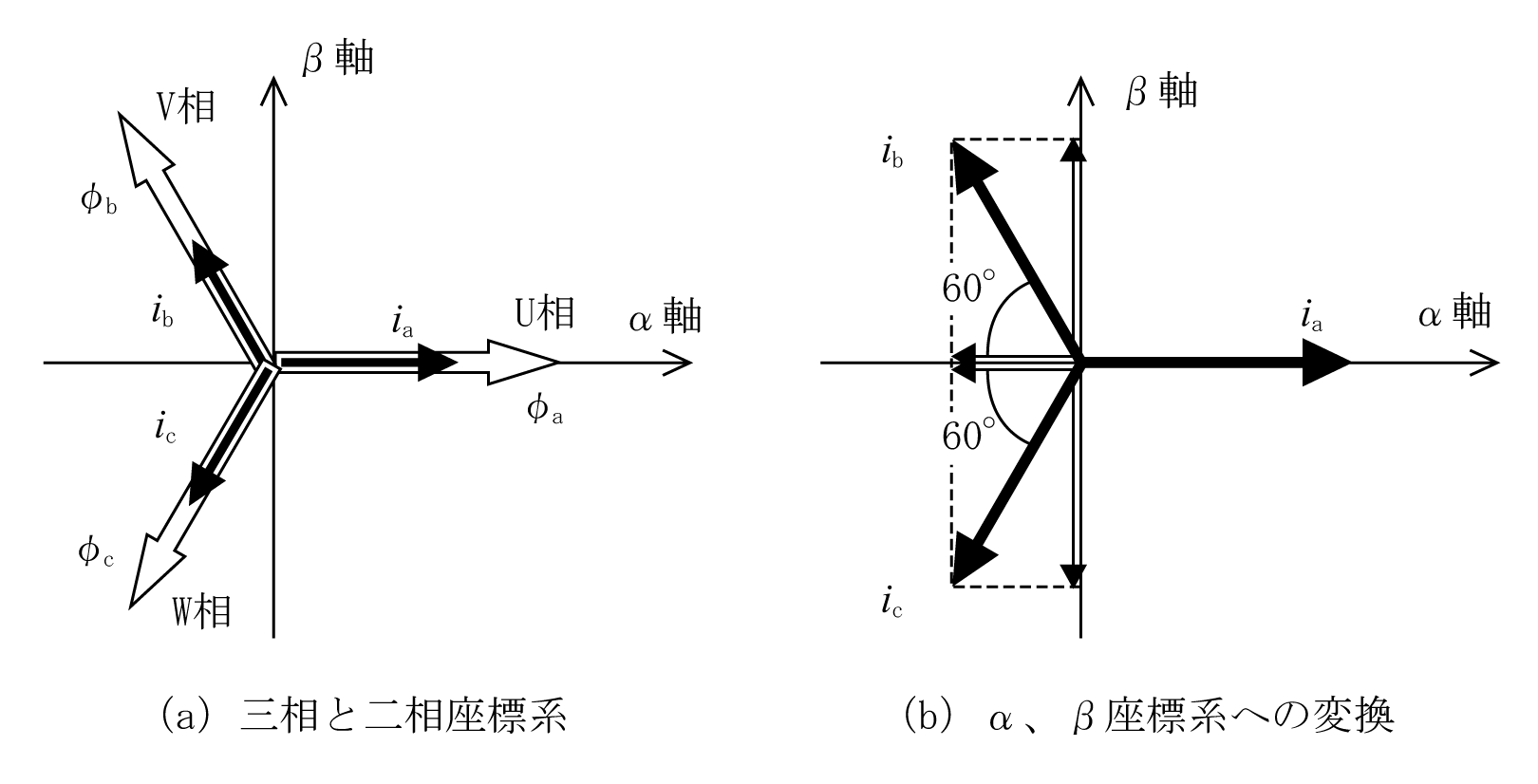
三相二相変換は対称三相交流をそれと等価な二相交流への変換で、αβ変換と呼ぶ。第2図の三相モデルを第3図（a）のように直交するα軸とβ軸を考えα軸とU相軸を合うように配置する。
第3図（b）を参考にして固定子巻線に三相電流ia、ib、icがそれぞれ流れている状態を二相座標系のα軸、β軸で表現する。
α方向の電流iαはiaとibのα成分 －ib×cos60°=－1/2×ibと、ic のα成分 －ic×cos60º=－1/2×icの総和になる。同様にしてiβはibのβ成分
と、icのβ成分
の和となる。
以上をまとめると、
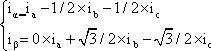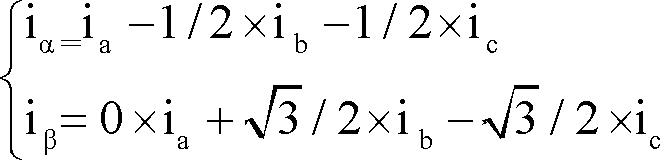（1）
（1）
となる。これを行列で表現すると、
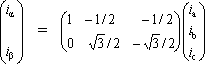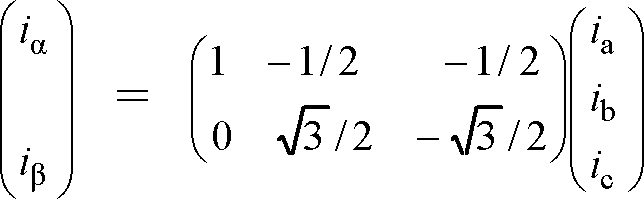（2）
（2）
である。確認のために右辺にある2個の行列の掛け算を実行すると、
（3）
（3）
となり、iα、iβに関する（1）式が再現される。
（2）式によりia、ib、icの三相電流の状態をiα、iβの二相電流で表現できたことになる。この操作が三相から二相への座標変換であり、変換に使われた行列を変換行列という。
座標変換の条件として、変換前後で電気的・磁気的に等しい条件を付け加える。このような変換を絶対変換という。具体的には（2）式の座標変換に実数Kを掛けて、
（4）
として、これを三相二相の絶対変換とする。ここで〔 〕内のCは変換の記号で、そのほかの付属記号は後でまとめて説明する。絶対変換の条件は変換と逆変換を行うと元に戻るという次式で表現される。
（5）
（5）
ここで[1]は行列の対角要素が1、そのほかの要素が0の行列で、[ ]Tは転置行列を表し行と列を入れ替えた行列である。（5）式の左辺を計算する。
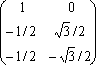
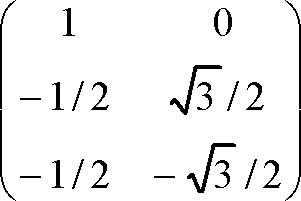
（6）
この結果を（5）式の左辺に置くと、K2×3/2 [1]=[1]でありK2×3/2=1、すなわち
と求められる。これより、三相から二相への絶対変換は（7）式の行列で表現される。
（7）
（7）
既に簡単な説明の基で使用したが、今後使用する記号について整理しておく。
[ ]は行列を、Cは変換を意味して、[C]で変換行列とする。上付きや下付きの文字は座標系を表す。これらを組み合わせた [αβCabc]は、a、b、c軸座標系からα、β軸座標系への変換行列を表わす。また、[αβi ]は電流をα、β軸座標系で表現した行列とする。
[ ]－1は逆行列を表す。[αβCabc]－1はa、b、c軸の座標系からα、β軸座標系への変換の逆の変換行列で[abcCαβ]と等価である。[αβCabc]－1=[abcCαβ]の関係である。
ここで、上付きと下付きの効用について説明しておく。上付き座標を分子に下付き座標を分母にして分数計算すると変換の答えになる。具体例で示すと、
[abci ]=[abcCαβ] [αβi ]の変換では、
が成立するので便利である。
なお、[A][A]T=[1]が成立する行列では [A]－1 = [A]Tが成立し、逆行列は転置行列と同等である。[αβCabc] = [abcCαβ]－1=[abcCαβ]Tとなるので、
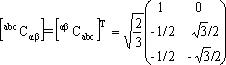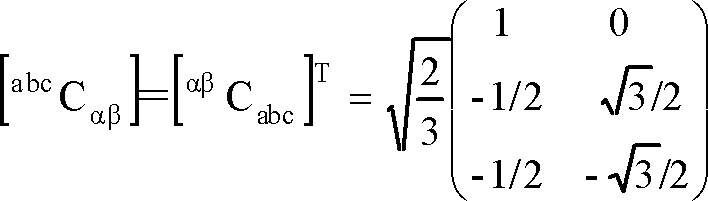（8）
（8）
は二相から三相への変換行列である。
幸いなことにこれから出てくる回転座標変換行列にも[C]－1=[C]Tが成立するので、両者を特に区別する必要はない。
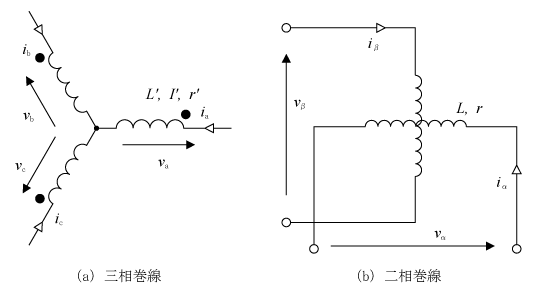
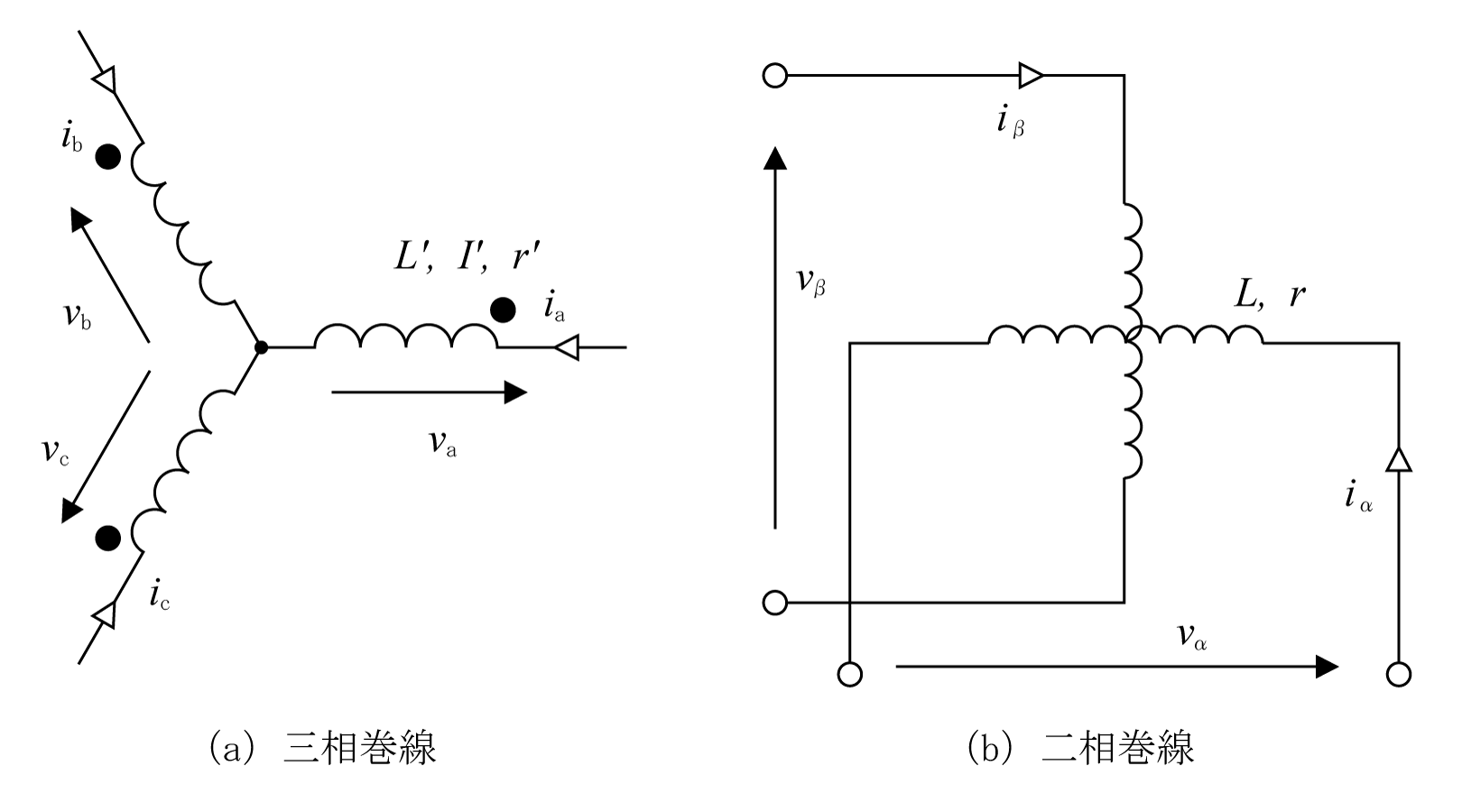
電圧や磁束についても上記の電流とまったく同様に三相巻線と二相巻線変換が可能である。電圧方程式の三相から二相への転換を実行する。第4図に両者を対比して示す。
第4図（a）の三相巻線の電圧方程式は次式になる。
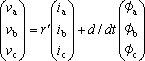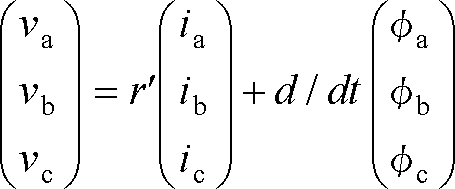（9）
（9）
ここで、r′ は巻線抵抗，φa、φb、φcは各相の鎖交磁束である。
1相当たりの漏れインダクタンスをl′、有効インダクタンスをL′とすると、各相の鎖交磁束は巻線の配置から次式となる。
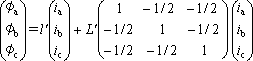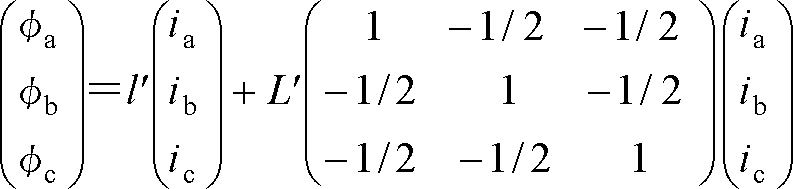（10）
（10）
ここで、φaへのib、icの電流寄与分はφb、φcのφa方向成分であり、－φbcos60°、－φccos60°の計算値である。φb、φcについても同様に確認できる。
（9）、（10）の行列を簡単に、
（11）
（11）
と表現する。
[abcv]に左から三相二相変換行列を掛けると、[αβCabc] [abcv] = [αβv]となり二相巻線に変換される。（11）式の右辺にこの変換を作用させる。
（12）
（12）
各項の計算を実行する。まず第1項は次のように計算される。
（12）式第1項=
（13）
ここでr′ は定数なので行列の積の前に移動できる。[αβCabc] [abcCαβ]は変換と逆変換なので、積は[1]である。また、[1] [αβi]=[αβi]になるのは、普通の計算と同じである。
αβ座標系での抵抗rと電流の関係はr[αβi]なので、係数の比較によりr=r′ が成立している。すなわち、三相二相変換では抵抗値は変化しない。続いて第2項は以下の展開になる。
（9）式第2項=
（14）
（14）
ここで、[abcCαβ]は定数行列なので時間微分の影響を受けなく、定数扱いで前方に出すことができる。よって、
であり、（11）式と類似な式になる。
以上により、この変換では電圧と磁束の関係式の形は変化しないことが分かる。
次に磁束φの式を変換する。
（15）
（15）
（15）式の[αβCabc] [abcL] [abcCαβ]はαβ座標系でのφとiの関係の係数なので、この座標系のインダクタンスとして、[αβL]であり、（10）式の[abcL]を代入して計算すると、
（16）
（16）
になる。
二相と三相変換では抵抗値は変化しないが，インダクタンス値は絶対変換の影響を受けて変化する。
第4図（b）から二相巻線で電圧方程式をたてると、
（17）
（17）
である。行列が3×3から2×2に変数の数が減り、しかもインピーダンス行列は対角行列になって三相巻線の場合と比較して大幅に簡単化されている。これは解析の容易性だけでなく、システム制御での処理時間短縮に寄与しており、二相変換が使用される理由である。
（1） 電気学会 交流電動機駆動方式の技術・分類・用語整理調査専門委員会編:交流電動機可変速駆動の基礎と応用、コロナ社刊
（2） インバータドライブハンドブック編集委員会編:インバータドライブハンドブック、日刊工業新聞社刊