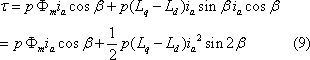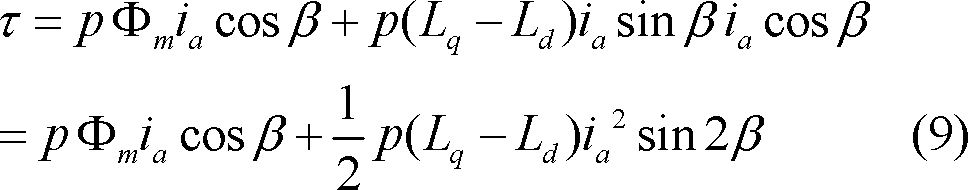PM同期モータは電機子巻線を固定子、回転子(ロータ)に永久磁石を使用した回転界磁形のモータをいい、永久磁石式モータ、磁石式同期モータなどとも呼ばれている。界磁電流が不要なため界磁損失がなく、本質的に低損失・高効率である。従来からACサーボなどの小容量モータに多く採用されているが、最近は省エネルギー機器としてより大型のモータにも採用される傾向にある。
表面磁石構造の同期モータ(SPMSM)と埋込磁石構造の同期モータ(IPMSM)に大別され、ここでは両構造の概要とIPMSMの詳細な特性について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your
Flash plugin.
※テキスト中の図はクリックすると大きく表示されます

直流モータは界磁用の永久磁石が固定子に、電機子巻線が回転子に配置される回転電機子形であるが、PMSM(Permanent Magnet Synchronous Motor)は永久磁石を回転子に、電機子巻線を固定子に設けた回転界磁形の構成である。
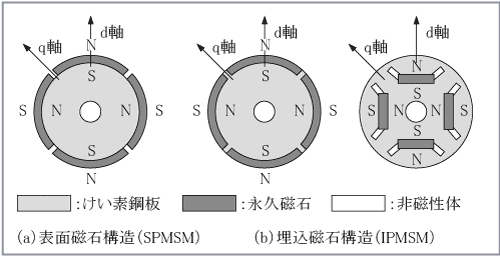
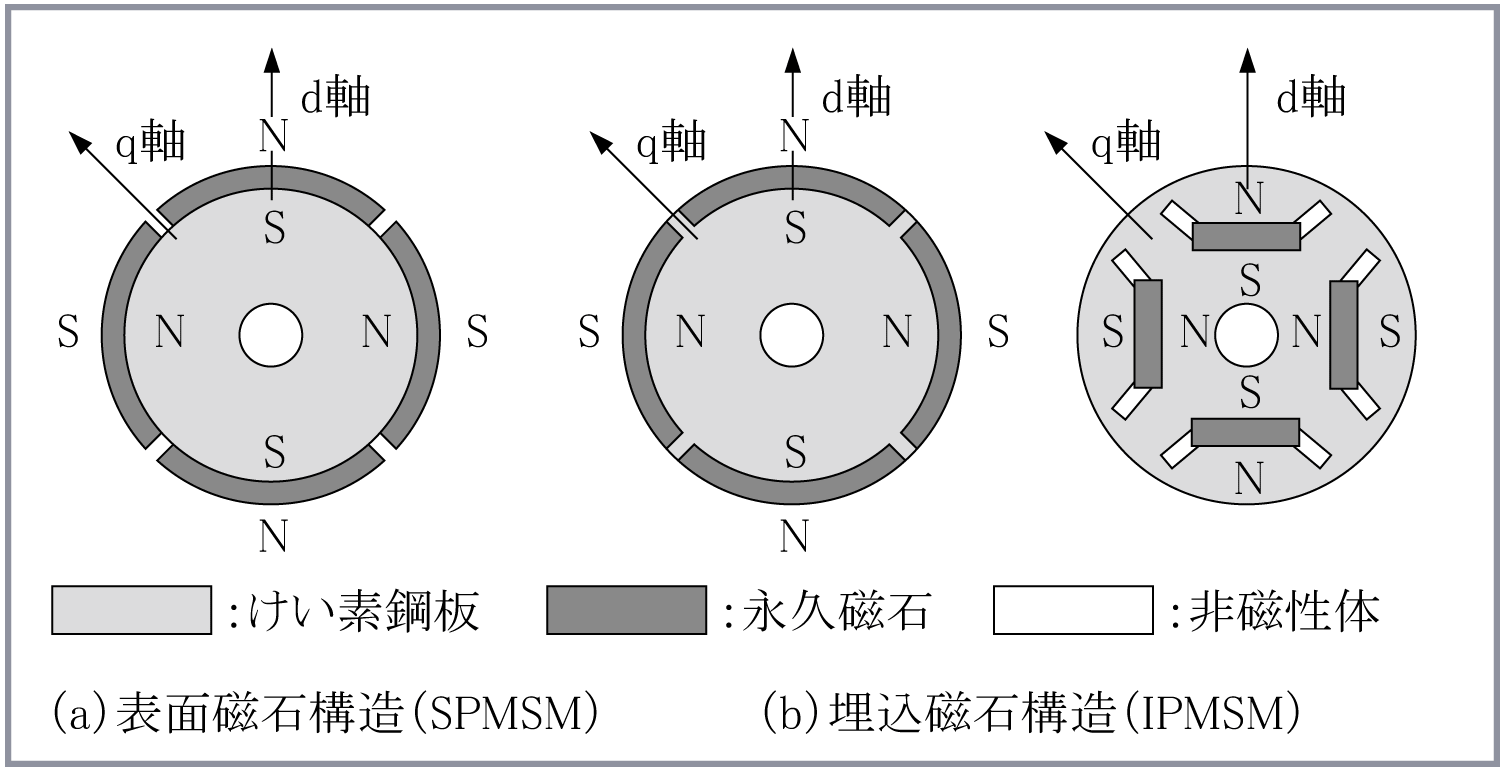
回転子はけい素鋼板から成る鉄心とその中に配置された永久磁石から成る。永久磁石の配置から、回転子の表面に永久磁石を張り付けた表面磁石構造の同期モータ(SPMSM:Surface Permanent Magnet Synchronous Motor)と回転子の内部に永久磁石を埋め込んだ埋込磁石構造の同期モータIPMSM(Interior Permanent Magnet Synchronous Motor)に大別される。第1図に代表的な回転子構造を示す。
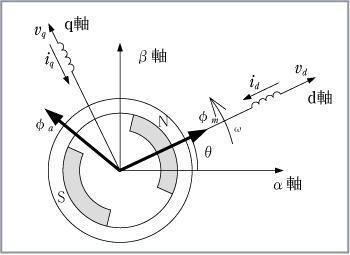
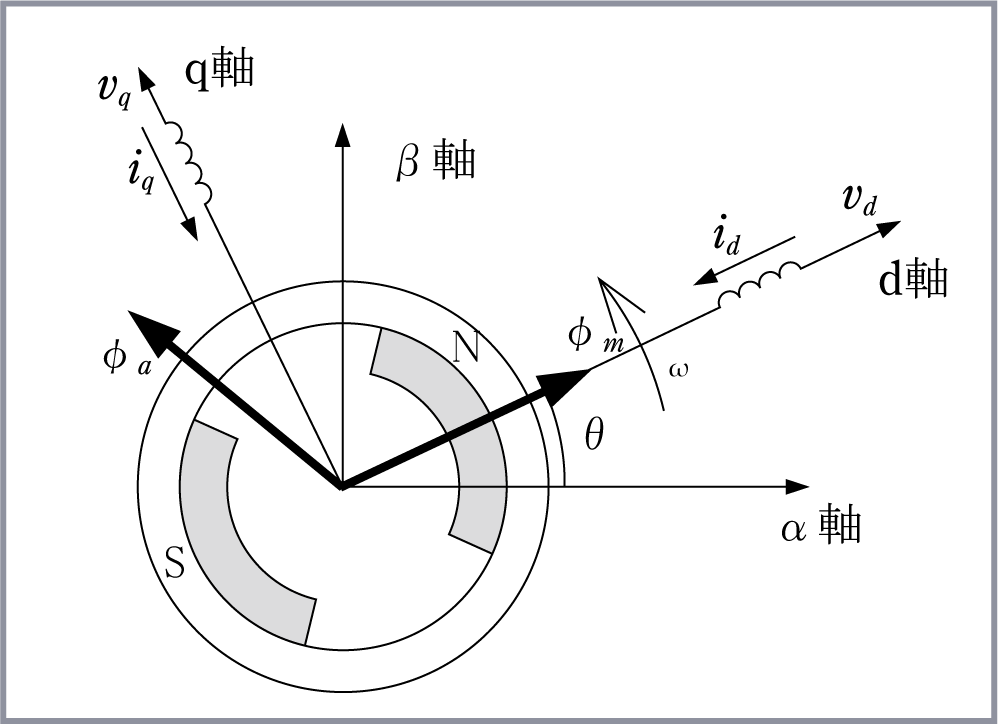
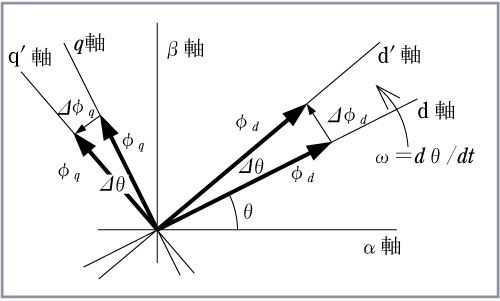
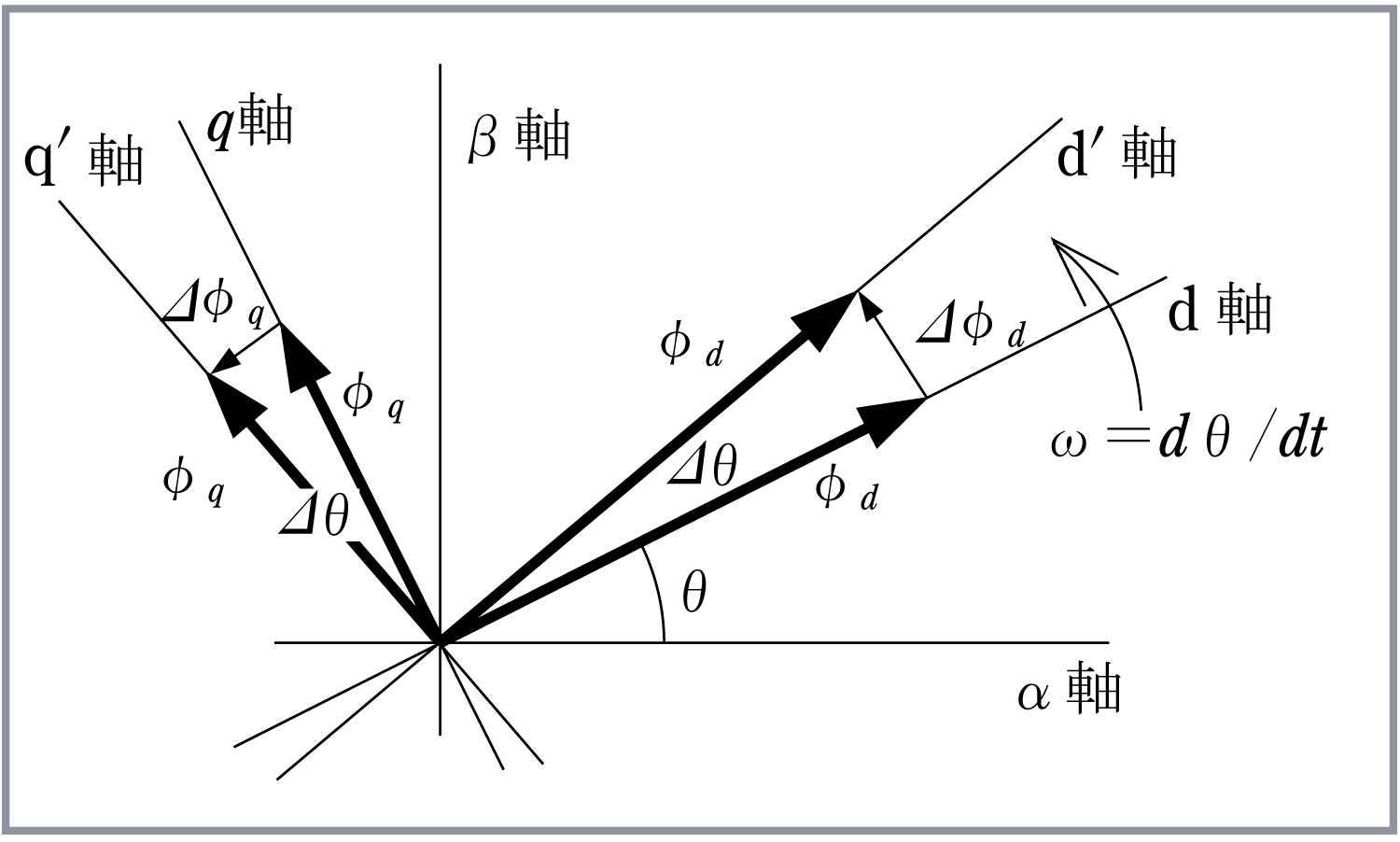
ここで、回転子の磁極の軸を図のように、磁極がつくる磁束の方向(永久磁石の中心軸)をd軸とし、それと電気的、磁気的に直交する軸(永久磁石間の軸)をq軸に設定する。
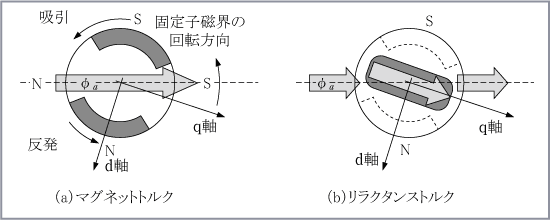
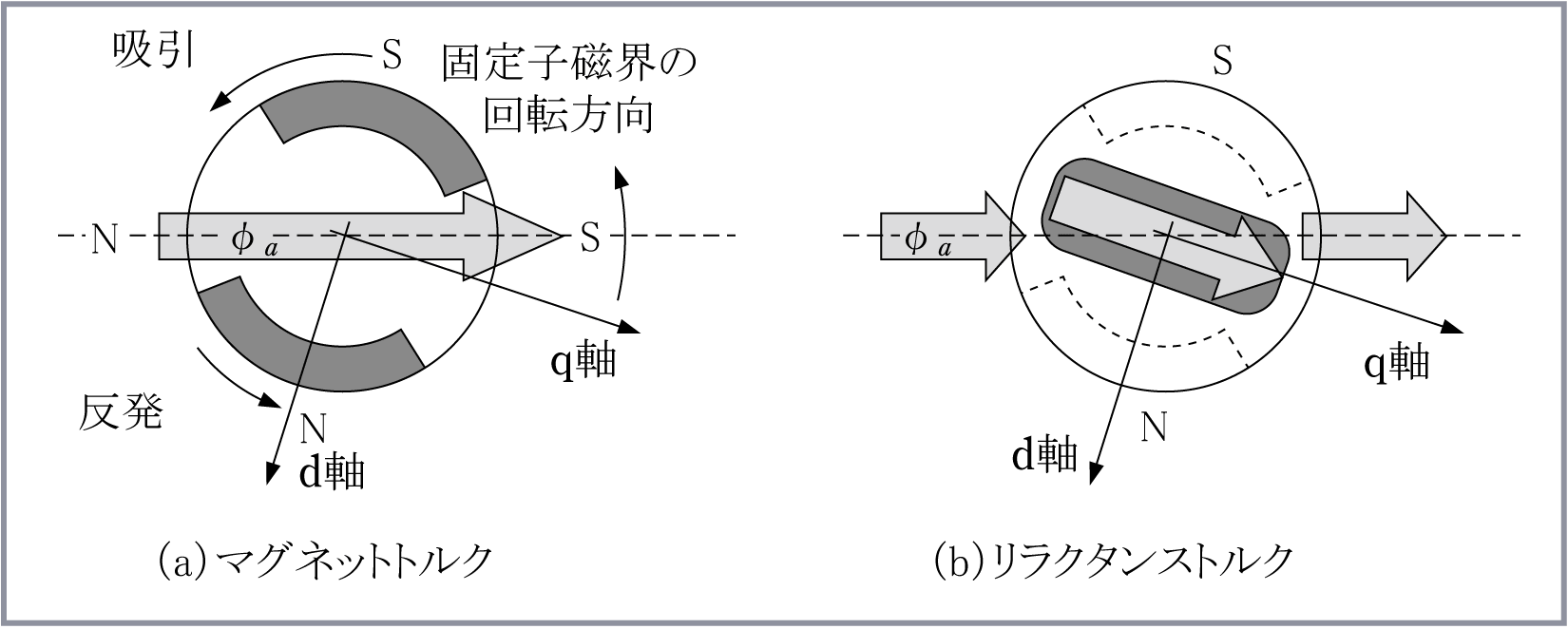
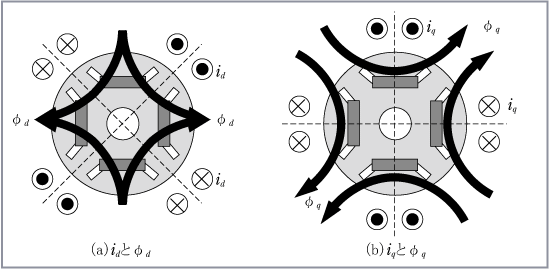
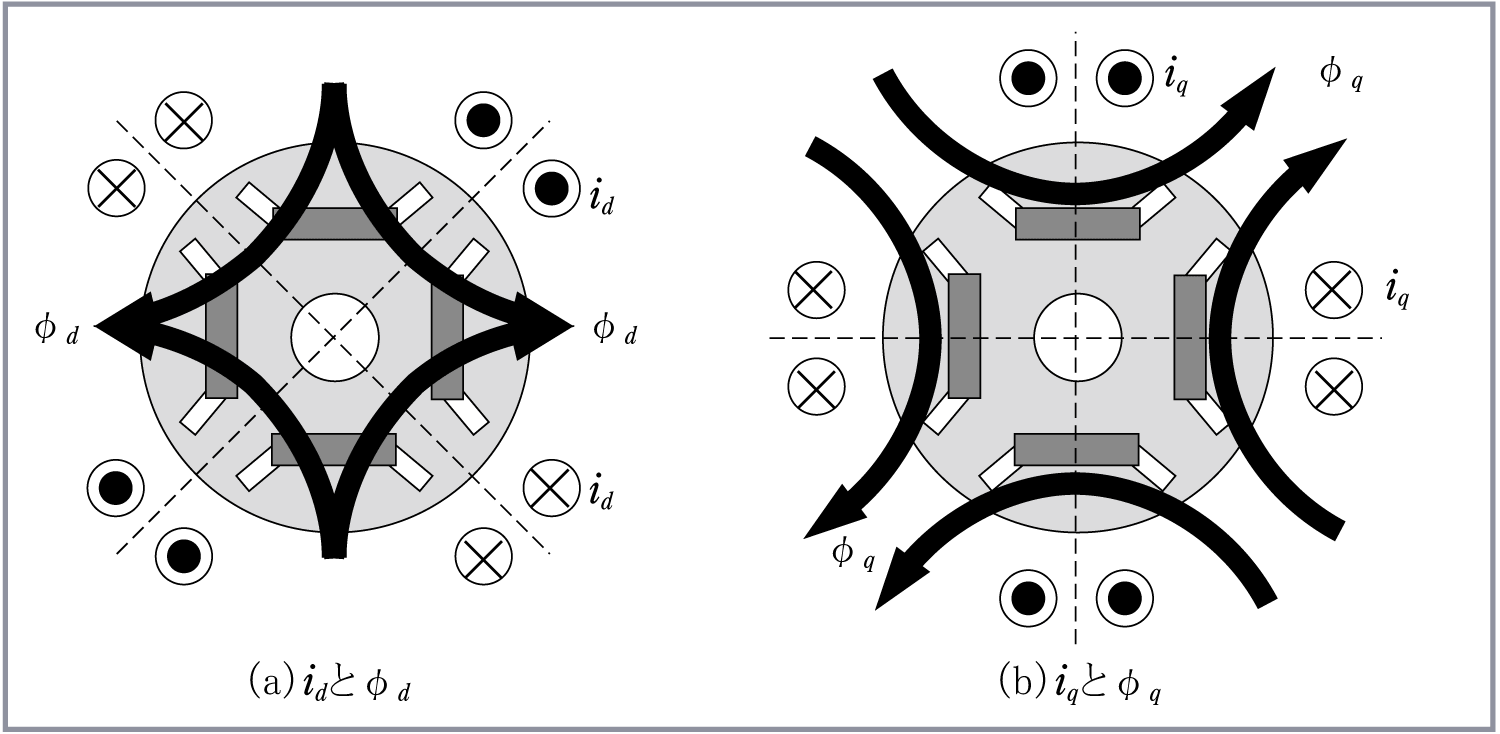
IPM同期モータでは永久磁石によるトルクのほかにリラクタンストルクが発生する。第2図は固定子巻線電流による回転磁界と回転子の位置を表現している。
図(a)はマグネットトルクを、図(b)はリラクタンストルクの発生状況を示す。永久磁石の透磁率は真空中の透磁率とほぼ等しいため、永久磁石の部分は磁気的にエアギャップと等価になる。そこで図(b)では埋込磁石の影響を実効的なけい素鋼板の形状に変形し、d軸側を磁石に相当する分だけ縮小して示す。
マグネットトルクは、図(a)に示すように回転磁界の極と回転子の永久磁石の磁極との吸引及び反発によって発生する。
リラクタンストルクは固定子の回転磁界による極と回転子の突極との吸引力だけによって生ずるトルクで、図(b)ではq軸が固定子磁界のS極に吸引される。これは磁路の磁気抵抗(リラクタンス)が小さくなる方向であって、回転子の極のS、Nに関係していない。

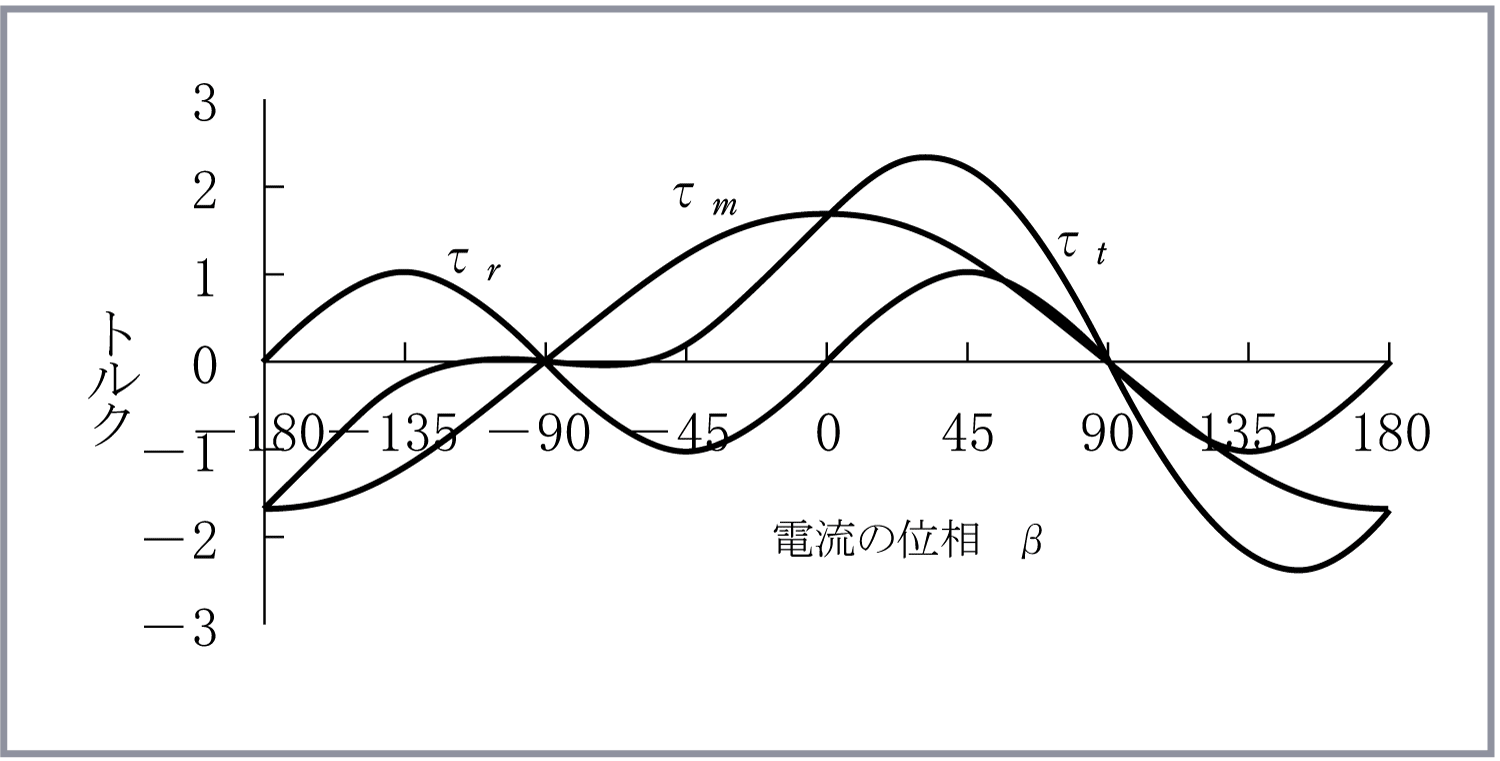
第7図に電流一定の状態で、電流位相角βを変化させたときのマグネットトルク
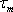
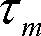
、リラクタンストルク
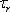
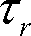
、全発生トルク
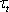
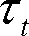
をグラフ化して示す。
マグネットトルクはβ=0°で最大となり、β=180°でマイナス最大になる。一方、リラクタンストルクはβ=45°、−135°で最大、β=—45°、 135°でマイナス最大になる。その結果、全発生トルクは電流位相が0°<β<45°の範囲で最大で、135°<β<180°で負の最大トルクとなる。
このようにβを変化する方式を電流位相制御といい、電流ベクトルを負荷条件に合わせて適切に選択することで、広い負荷範囲で高性能運転を可能にしている。

IPM同期モータでは前述のように
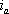
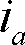
とβを制御することで各種のモードの運転ができる。電流制御方式とその制御条件の例を紹介する。
(1) 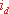
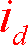 =0制御
=0制御
d軸電流を0に保つ制御で、電流ベクトル
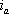
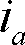
は負荷状態に応じてq軸上を移動する(第6図を参照)。発生トルクは(9)式にβ=0を代入することで、
となり、トルクがq軸電流だけに比例する線形制御になる。
SPM同期モータでは一般的な制御法であり、トルクの発生に寄与しないd軸電流を流さないため、同一トルクの条件では最小の電流となり、高効率運転になる。しかし、IPM同期モータではリラクタンストルクが利用できないので、必ずしも適切な制御とはいえない。
(2) 最大トルク電流制御
同一電流に対して発生トルクを最大に制御する方法で、これは電機子電流に対して最も効率的にトルクを発生する条件になる。
トルクの式(9)式をβで微分し、ゼロとした状態である。すなわち、
三角関数公式
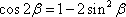
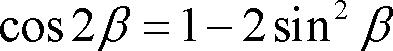
を代入して
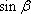
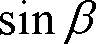
の二次方程式を解くことで、
が得られる。これが最大トルクを与える電流位相角である。このようにβを制御することで最大トルク運転になる。
(3) 弱め磁束制御
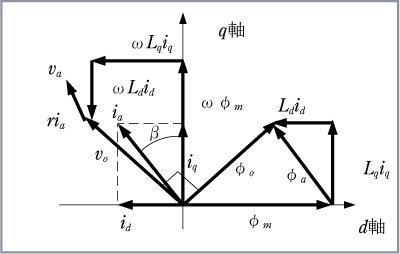
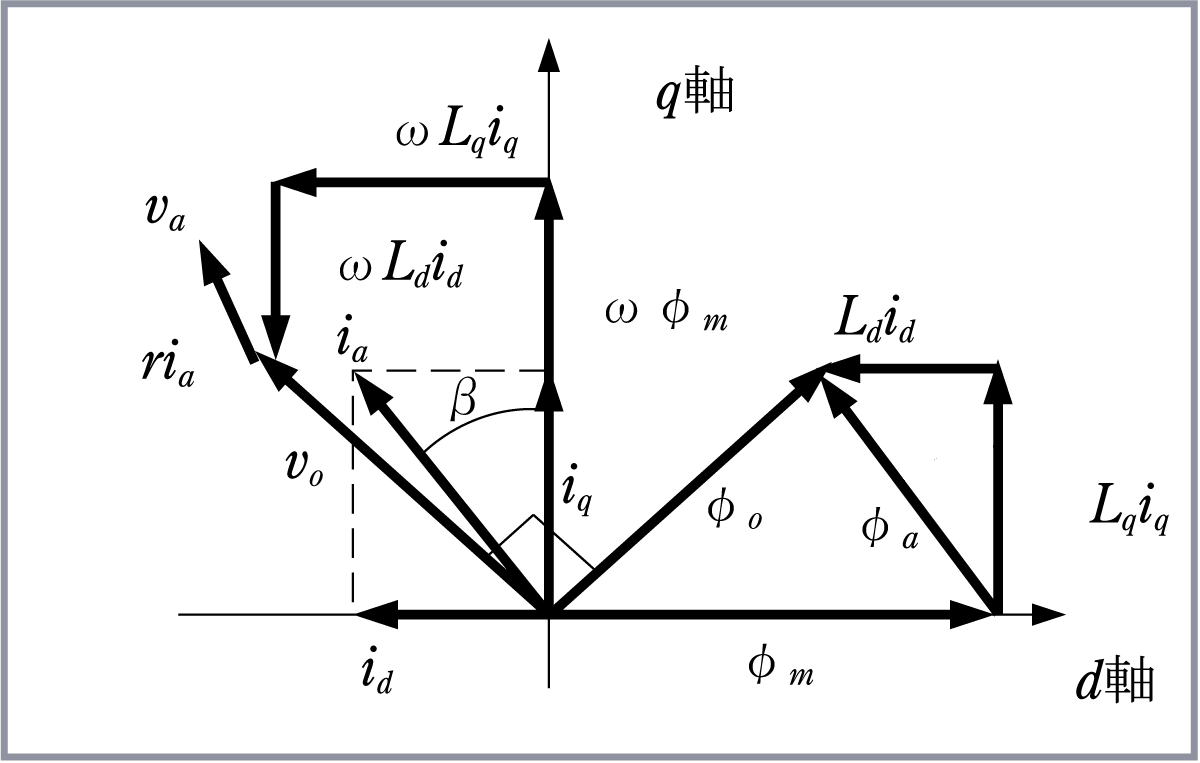
ベクトル図から分かるようにd軸の総磁束は
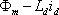
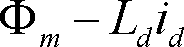
であり、d軸電流は永久磁石の磁束を減磁している。これは弱め界磁作用となり、総合磁束
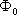
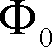
を減少させる。高速回転領域での誘起電圧の上昇を抑えてインバータの耐圧条件を緩和する制御として使用される。
参 考 文 献
- 武田洋次、松井信行、森本茂雄、本田幸夫:埋込磁石同期モータの設計と制御 オーム社刊
- 百目鬼茂雄:省エネ、高機能化へ高効率モータ技術 日刊工業新聞社刊
- (株)日立製作所総合教育センタ技術研修所編:わかりやすい小型モータの技術 オーム社刊
- 竹下隆晴、野村尚史、松井信行:電流推定誤差に基づくセンサレスブラシレスDCモータ制御 電学論D、115巻4号、平成7年
- 竹下隆晴、市川誠、李宙柘、松井信行:速度起電力推定に基づくセンサレス突極型ブラシレスDCモータ制御 電学論D、117巻1号、平成9年