確かに、テブナンの理による方法、対称座標法による方法、直接求める方法は、それぞれの特徴があり、注意すべき点も異なります。
ここでは、違いがしっかり身につくように極力似通った方法で解き、併せて特徴・注意事項について 簡単に説明します。
また、実務面で必要になる保護リレー(特に、方向地絡リレー(DGR))の入力電圧、入力電流について、参考として簡単に触れたいと思います。
① 回路のイメージ
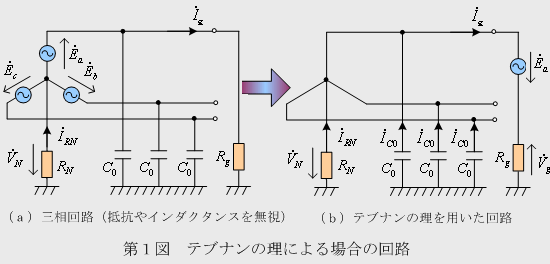
② 計算式の流れ
・第1図(b)から(1)~(4)式
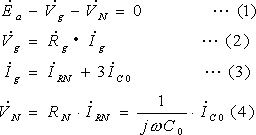
![]()
・![]() について整理((1),(2),(4)式)
について整理((1),(2),(4)式)
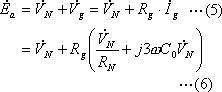
![]()
・![]() ,
,![]() の式
の式
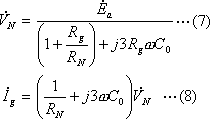
![]()
・DGRの入力電圧![]() ,入力電流
,入力電流![]()
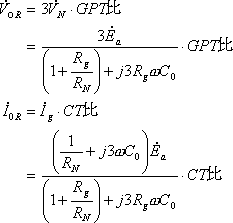
③ 特徴
- 配電系統のように非接地系統では、テブナンの理を活用して零相電圧を求めることができます。(RN(第1図(a)の中性点抵抗)が、多くの場合、等価的に10kΩ程度と大きく線路や変圧器の抵抗(R)、インダクタンス(L)等を無視できるので、テブナンの理を用いて計算できます)
- テブナンの理を用いると簡単に零相電圧(ここでは、(7)式の
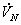 )を求めることができます。
)を求めることができます。
- 注意点は、第1図に示すように、
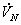 は
は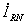 と逆向きになっていることです。
(式では(4)式のとおり、
と逆向きになっていることです。
(式では(4)式のとおり、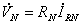 となる。対称座標法の
となる。対称座標法の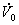 とは逆向きなので注意。)
とは逆向きなので注意。)
- DGRの入力電圧は、GPTの原理から各相電圧の和(ベクトル和)なので、結局3
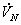 となる。(GPT比は、製品や各会社によって異なる場合があるので注意が必要です)
となる。(GPT比は、製品や各会社によって異なる場合があるので注意が必要です)
- DGRの入力電流は、ここでは
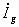 のみとしている。
のみとしている。
① 回路のイメージ
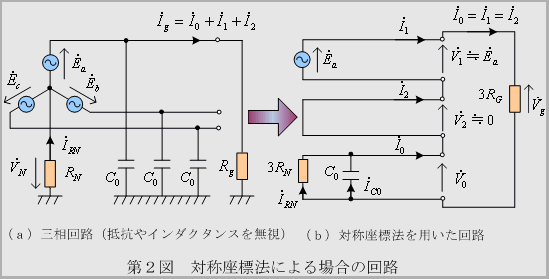
② 計算式の流れ
・第2図 (b)から(9)~(12)式
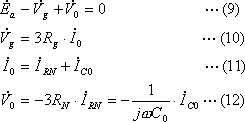
![]()
・![]() について整理((1),(2),(4)式)
について整理((1),(2),(4)式)
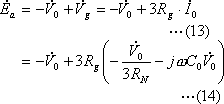
![]()
・![]() ,
,![]() の式
の式
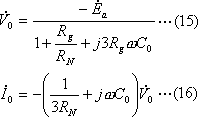
![]()
・DGRの入力電圧![]() ,入力電流
,入力電流![]()
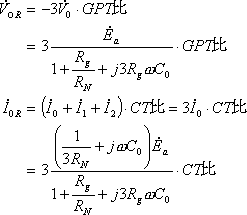
③ 特徴
- 66kV以上等の特別高圧系統では、もっぱら対称座標法を用いて計算しています。(線路や変圧器の抵抗(R)、インダクタンス(L)等を無視できないため)
なお、対称座標法を用いる場合は、回路が平衡である必要がある。 - 対称座標法の場合の
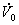 は、第2図のとおり
は、第2図のとおり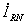 と同じ向きになっている。(式では(16)式のとおり、対称座標法の定義から、
と同じ向きになっている。(式では(16)式のとおり、対称座標法の定義から、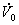 と
と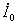 は逆向きになる)
は逆向きになる)
- (15)式のとおり、
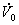 と
と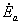 も逆向きになるが、リレー入力電圧は、テブナンの理と同じになる。
も逆向きになるが、リレー入力電圧は、テブナンの理と同じになる。
- リレー入力電流は、3の係数がつくが結果は、テブナンの理と同じになる。
- 対称座標法は、定義や計算法をしっかり修得する必要があるが、幅広く適用できる。
① 回路のイメージ
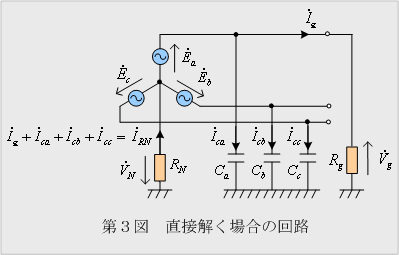
② 計算式の流れ
| ・第3図から |
||
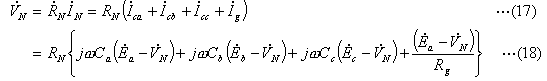 |
||
| ・ |
||
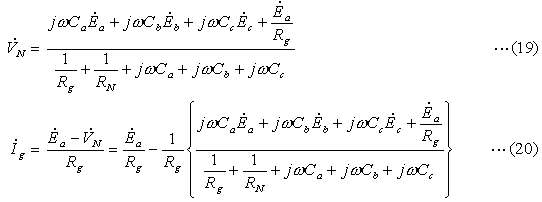 |
||
| ・DGRの入力電圧 |
||
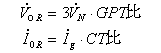 |
||
③ 特徴
- Ca,Cb,Ccの不平衡が無視できないときに、この方法を用いる場合がある。
- ここでは地絡事故時(Rgにて接地)を想定しているが、Rg=∞とすると常時の
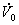 となる。
となる。
- シンプルな回路なので、直接解いてもさほど複雑な式にはなっていませんが、回路が少しでも加わると複雑な式になります。
- 紙面の都合上、細かな説明は省略していますが、ここではそれぞれの方法が理解・対比が出きるように同じような流れで
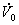 、
、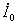 、DGRの入力電圧(
、DGRの入力電圧(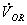 ),入力電流(
),入力電流(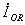 )、等を求めました。
)、等を求めました。
- 方向や係数について、違いがありますのでご注意下さい。 もちろん、いずれの方法で求めてもDGRの入力電圧(
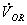 ),入力電流(
),入力電流(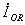 )は、同じになります。
)は、同じになります。
- 配電系統の零相電圧(
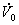 )を求める場合、GPT(接地変圧器)の変成比、3次回路の抵抗(R)によって、等価的な中性点抵抗値が異なります。実務面ではこれらについてもご注意下さい。
)を求める場合、GPT(接地変圧器)の変成比、3次回路の抵抗(R)によって、等価的な中性点抵抗値が異なります。実務面ではこれらについてもご注意下さい。
(参考1)としてGPT3次抵抗の中性点抵抗への換算例を示します。
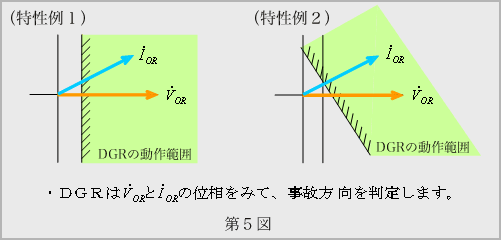
(参考2)としてDGRの判定例を示します。
(参考1) GPT3次抵抗の中性点抵抗への換算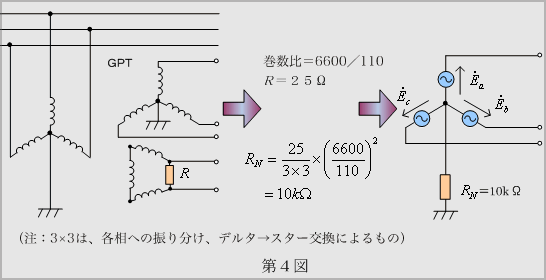
(参考2) DGRの判定方法