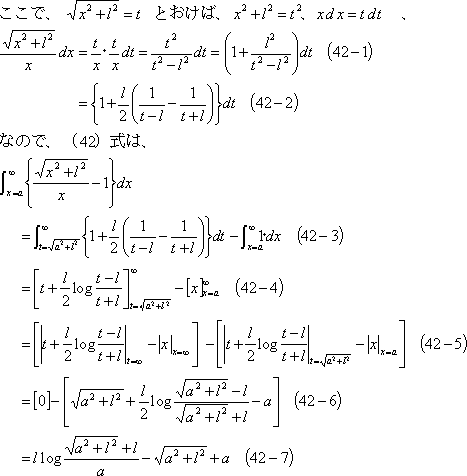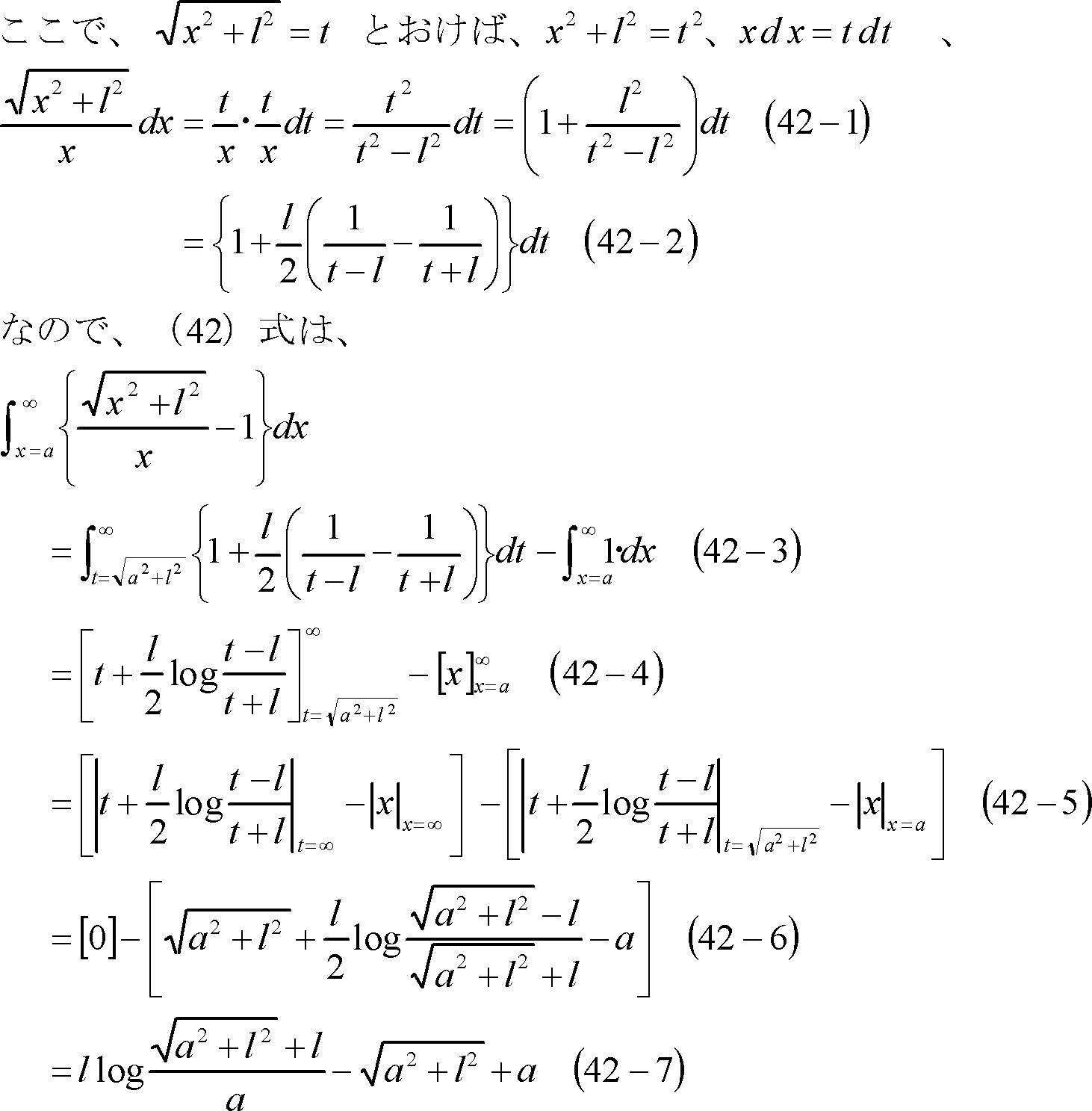〜終わり〜
■ぜひアンケートにご協力下さい■


電磁誘導現象は電気のあるところであればどこにでも現れる現象である。このシリーズは電磁誘導現象とその扱い方について解説する。今回は、代表的な磁気回路のインダクタンスの求め方について解説する。
自己インダクタンスを求めるための計算手順は第1図となる。
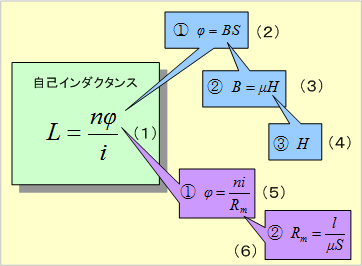
第1図 自己インダクタンスの計算手順
なお、計算の対象となる導体や線路の周囲の媒質は空気とする。
第2図のような環状ソレノイドがある。材料の透磁率μ、巻数N、平均半径R[m]、断面積S[m2]であるとき、このソレノイドの自己インダクタンスはいくらになるか。
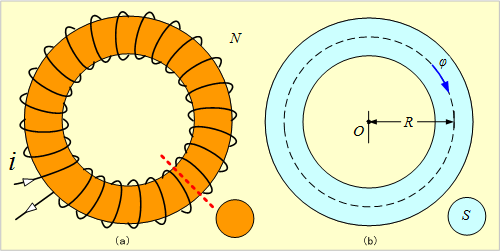
第2図 環状ソレノイド
同図(a)に示す方向に電流i [A]を流すと、同図(b)のようにソレノイド内に磁束φができる。φは磁路の長さをl [m]とすれば、磁気のオームの法則により、
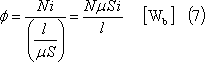
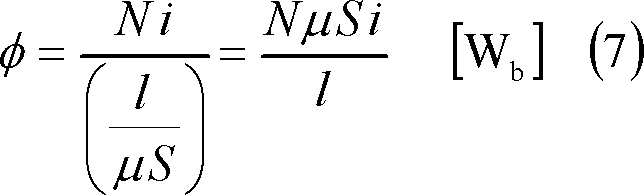
であり、自己インダクタンスLは、
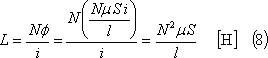
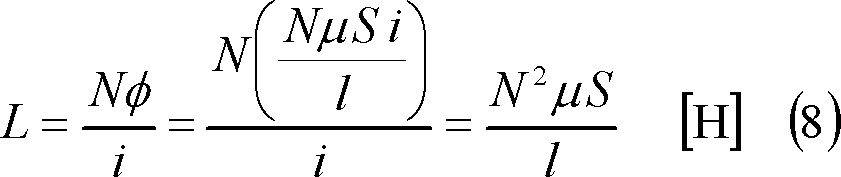
となる。ここで、磁路断面の半径をr[m]とすれば、Lは次式となる。
第3図(a)のように、非常に長い空心円筒状のソレノイドの場合は、円筒内部は平等磁界となるので、単位長あたりの巻数をn[回/m]、空気の透磁率をμ0[H/m]とすれば、同図(b)において、次のオームの法則が成立する。
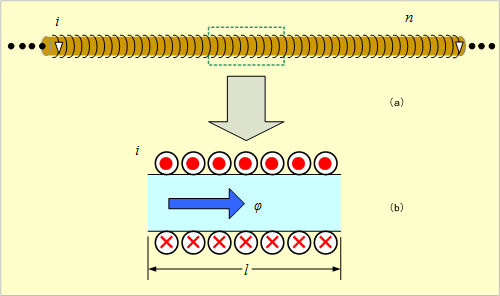
第3図 無限長円筒ソレノイド
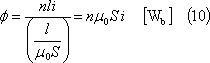
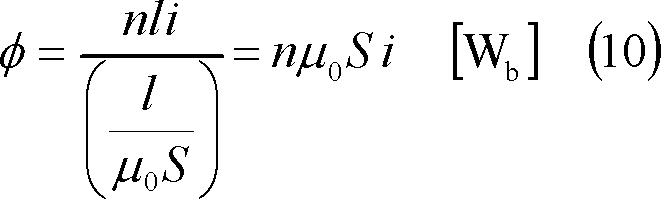
したがって、単位長あたりの自己インダクタンスLは次式となる。
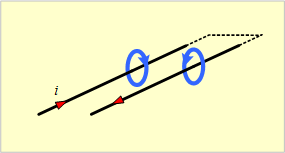
第4図 無限長直線導体による往復線路
第4図のように非常に長い直線導体2本を平行間隔D[m]で配置して往復線路とした場合の線路の自己インダクタンスを求めてみよう。
第5図(a)は線路の断面図で、導体に電流i [A]を流すと、各導体では図のように導体(赤色部)を中心とした同心円状の磁界ができる。したがって、この線路の自己インダクタンスは往復線路という1回巻きコイルと、これと鎖交する磁束φA、φBから求められる。いま、左側の導体Aに注目し、この導体と鎖交する磁束φAを求めてみよう。
同図(b)において、導体中心Oから距離xにおける微少距離Δxと導体長l[m]でつくられる微少面積ΔSを通る磁束ΔφAは、
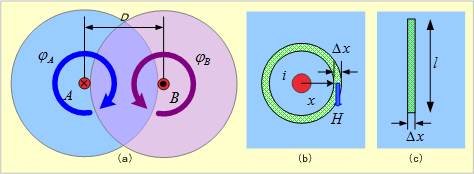
第5図 直線導体の往復線路
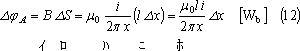
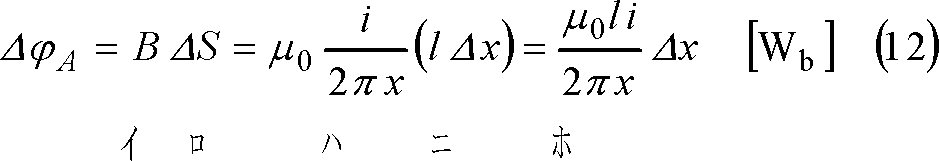
であり、導体が半径r [m]の円形断面をもつとすれば、φAは、
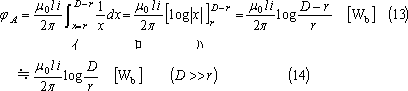
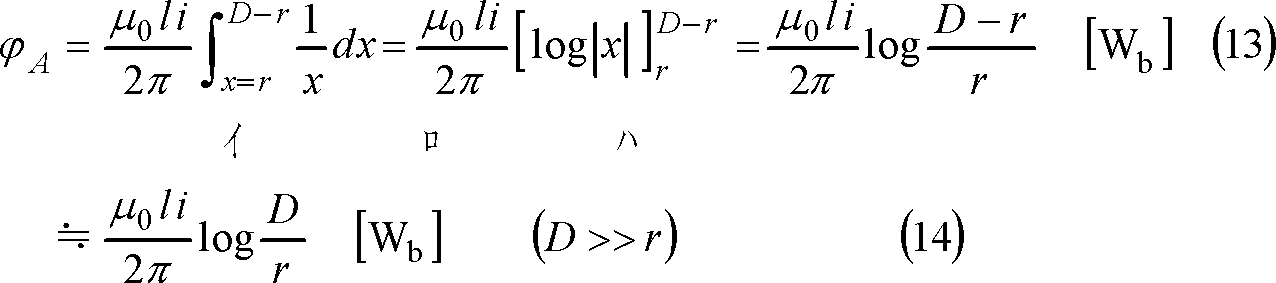
(13)式の注
積分公式
![]()
![]()
となる。この結果、線路導体1本l[m]の自己インダクタンスLは、次式となる。
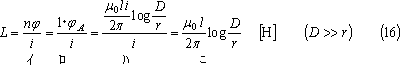
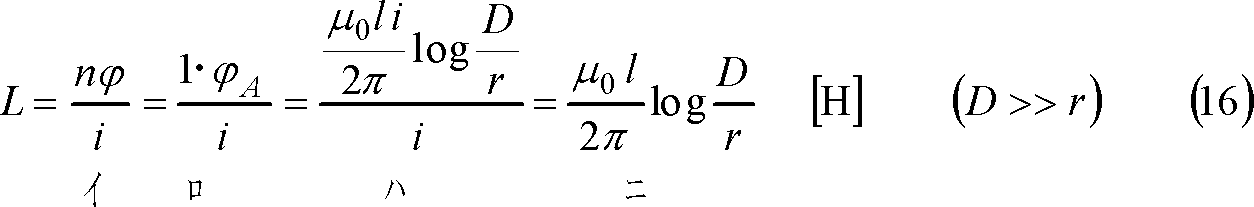
先に扱った直線導体は、第6図(a)のように導体内部を電流が均等に流れていると、同図(b)のように、導体内の一部Cを流れる電流と、この電流がつくる磁束が円筒形導体(茶色部)に同心円状にでき、この結果、電流と磁束が鎖交するので、そこにインダクタンスが存在することになる。このため、このような導体内部のインダクタンスを求めてみよう。
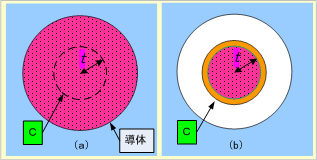
第6図 導体の内部にもインダクタンスがある
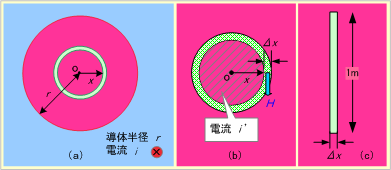
第7図 直線導体の内部
第7図(a)のように、導体(赤色部)の内部で中心Oからx[m]の部分で、微少厚Δx[m]と紙面と垂直な長さ1[m]とでつくる断面(緑色部)ΔS(同図(c))を通る磁束の磁束密度をB[T]、その内部(斜線部)を流れる電流をi´[A]、導体の透磁率をμとし、電流が導体断面を一様に流れているものとすれば、i´による磁束鎖交数
![]()
![]() は、
は、
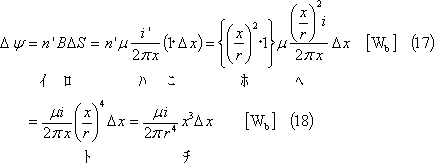
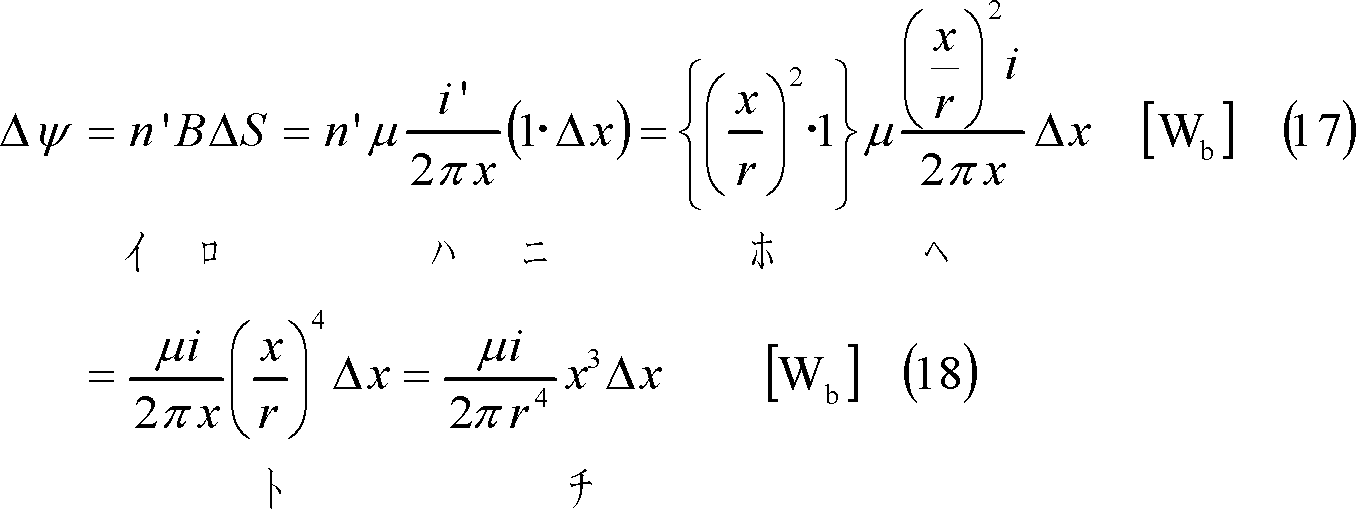
であり、導体内部の磁束鎖交数
![]()
![]() は、
は、
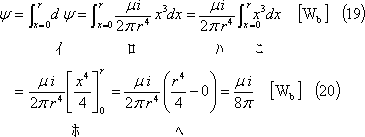
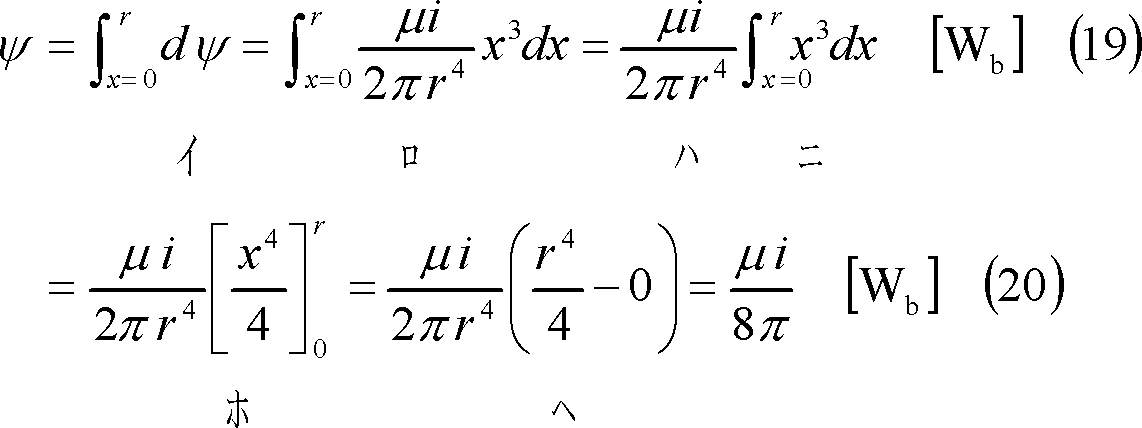
となる。したがって、導体1本l[m]の内部の自己インダクタンスLIは、
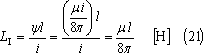
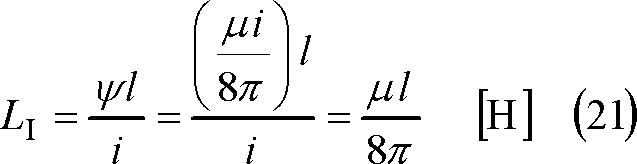
この結果から、導体はその内外に自己インダクタンスが存在することがわかる。したがって、非常に長い平行往復線路を形成する直線導体1[本]、l[m]の自己インダクタンスLは、次のようになる。
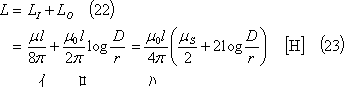
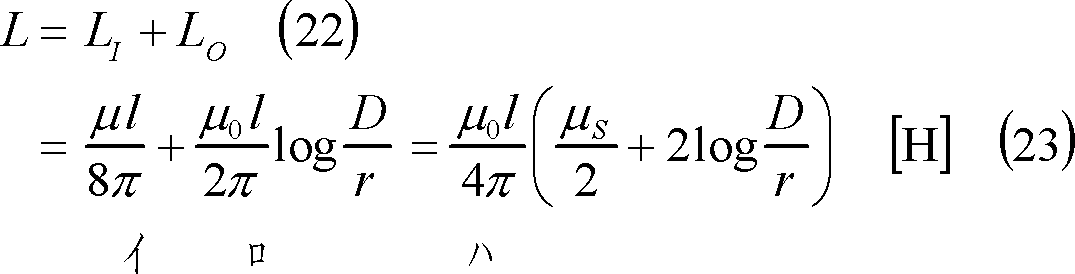
したがって、往復線路l[m]の自己インダクタンスLは、
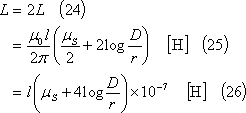
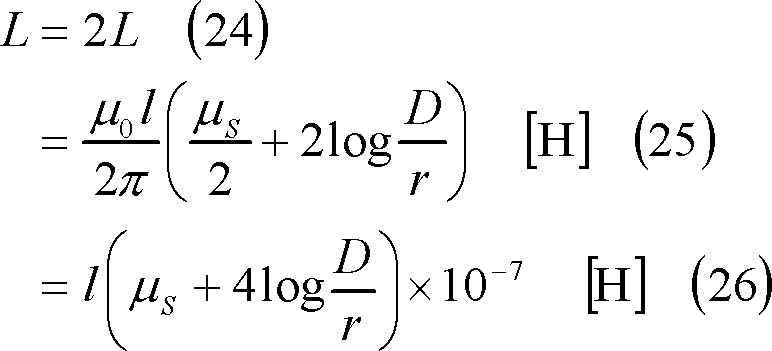
【例題1】 (23)式は、平行往復線路を形成する片側の直線導体1[本]、l[m]の自己インダクタンスLの式である。この式を使用して、線路1[km]あたりの自己インダクタンス[mH]を求める計算式を導け。ただし、対数は常用対数を使用するものとする。
[解答]
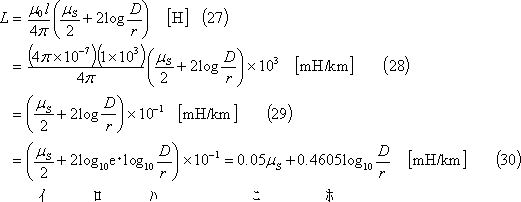
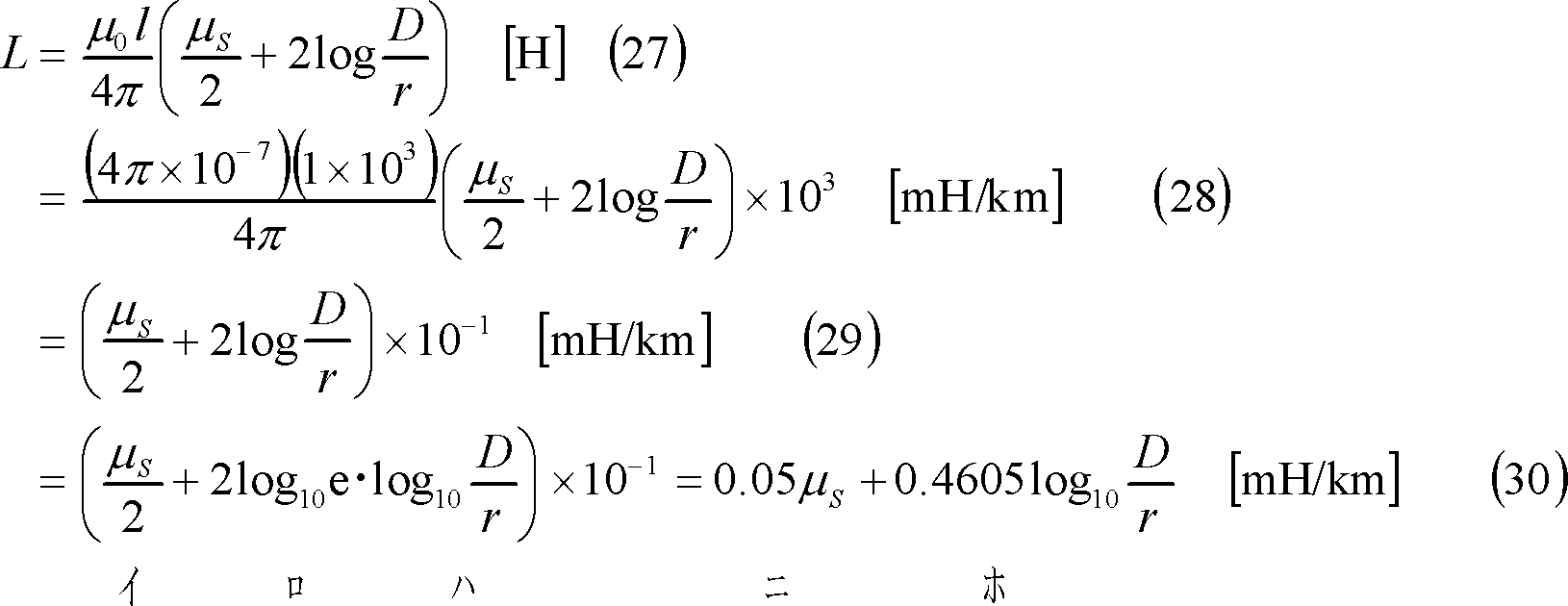
対数 (31)式の関係にあるとき、(32)式を「
![]()
![]() を底とした対数」という。
を底とした対数」という。
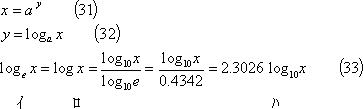
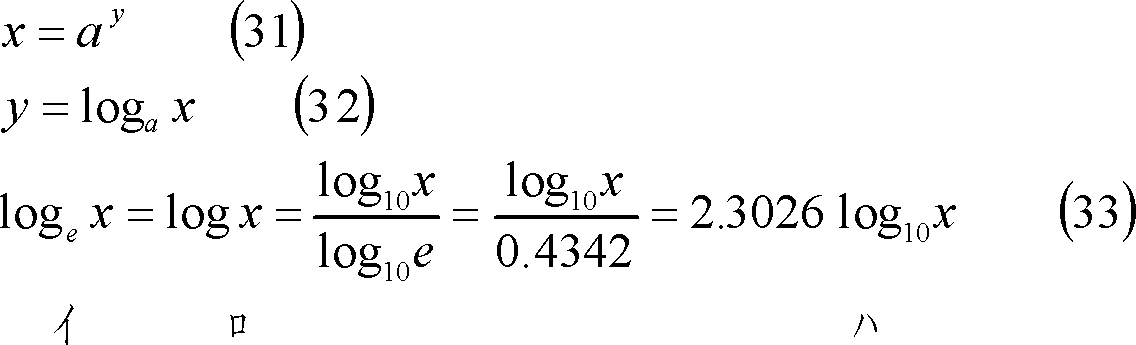
注 本講では特にことわらない場合、eを底とする対数を『
![]()
![]() 』と表記することにする。
』と表記することにする。
第8図のように、地表上h[m]に張られた直線導体で、大地を帰路とする往復線路の場合は、大地を完全な導体とみなせば、第9図(a)のような線路と考えられるので、導体と電流とは同図(b)の関係にあるから、直線導体の往復線路とみなせるので、その自己インダクタンスLは、
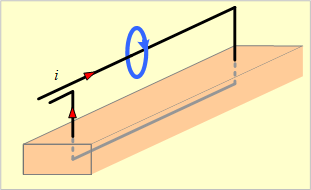
第8図
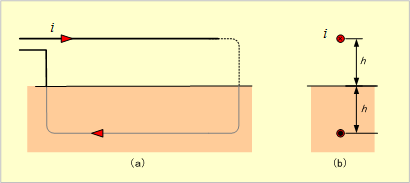
第9図
(23)式において、D=2hとおけばよく、次式となる。
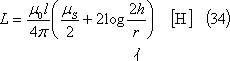
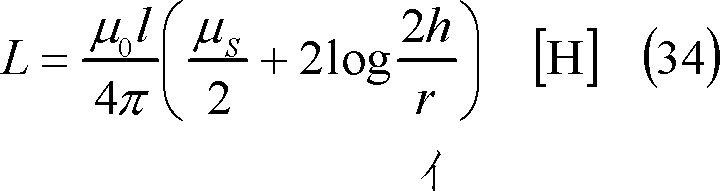
【例題2】 (23)式において、導体外部の自己インダクタンスは導体内部のおよそ何倍か。ただし、導体は銅線であり、導体の直径は1[cm]、導体間距離は5[m]とする。
[注] 銅の比透磁率
![]()
![]()
[解答] (23)式の右辺において、第2項と第1項との比は、
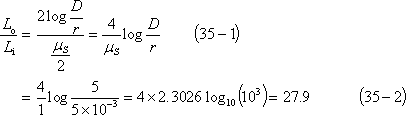
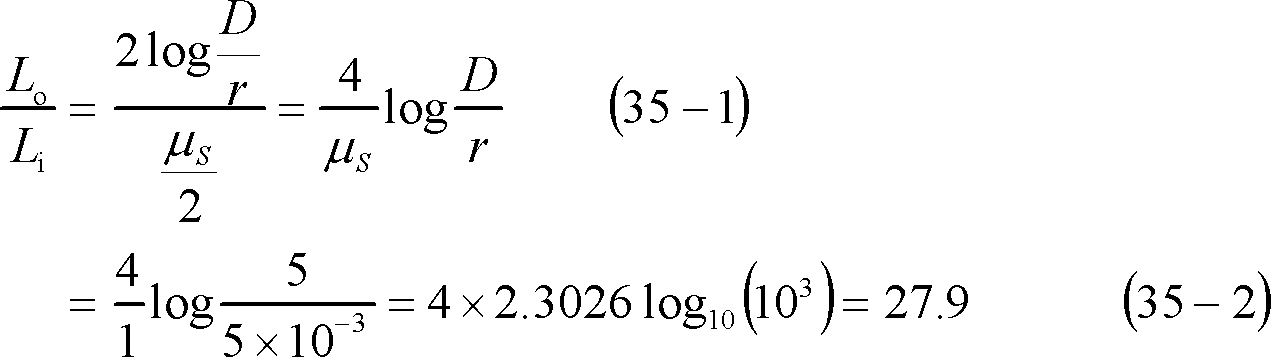
第10図のように、半径a[m]の円形断面をもつ直線導体で、長さl[m]部分の自己インダクタンスを求めてみよう。
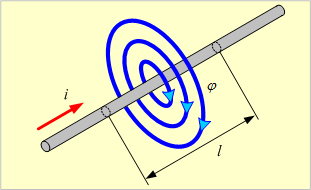
第10図 直線導体の自己インダクタンス
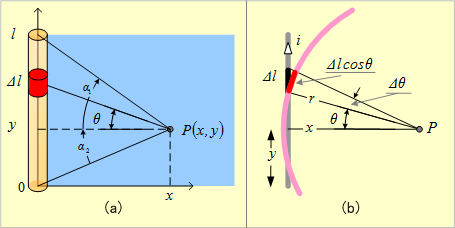
第11図 直線導体がつくる磁界
第11図(a)のように導体中心をXY座標のY軸に合わせ、その端が原点となるように置く。この導体がつくる磁界中(青色部)の点P(x,y)に、導体の微少長(赤色部)Δl [m]に電流i [A]が流れるためにつくる磁界ΔHは、
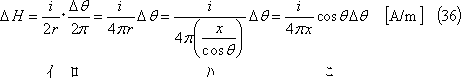
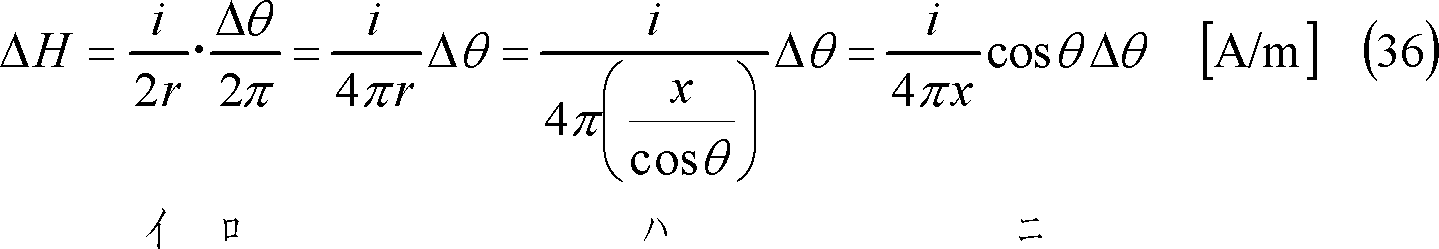
なので、導体l [m]がつくる磁界Hは、
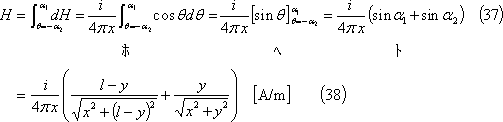
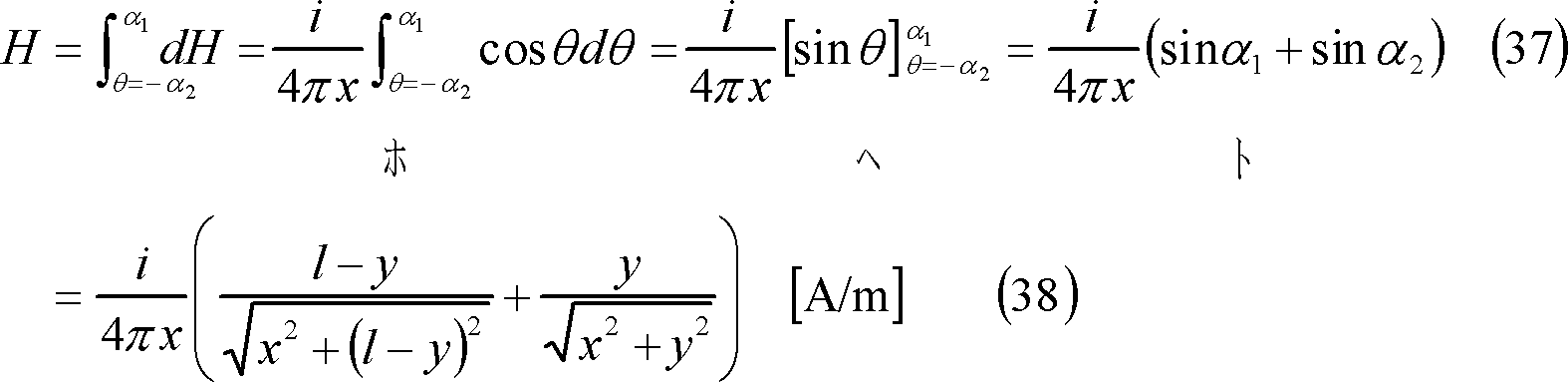
したがって、導体l [m]と鎖交する磁束φは次式となる。
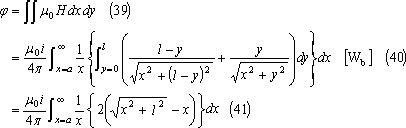
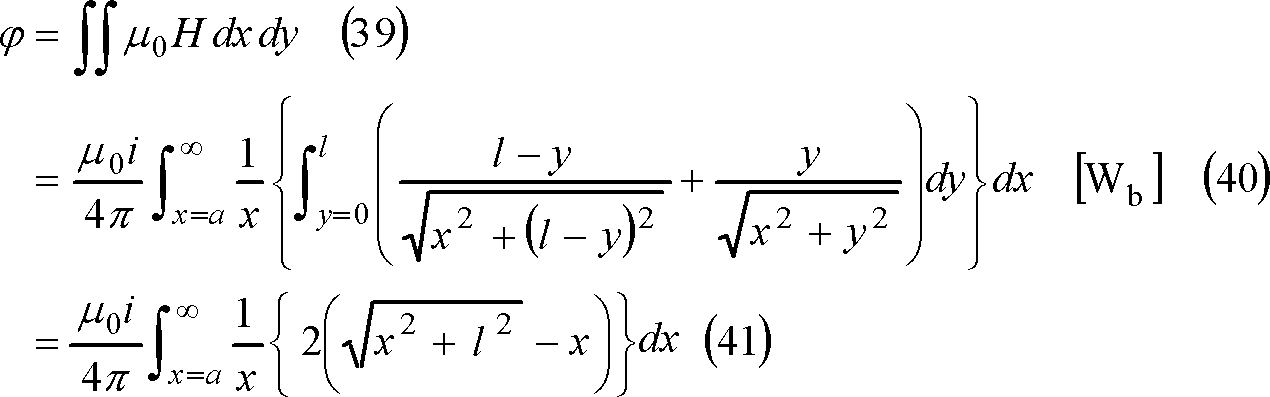
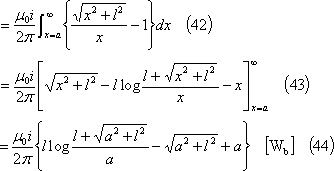
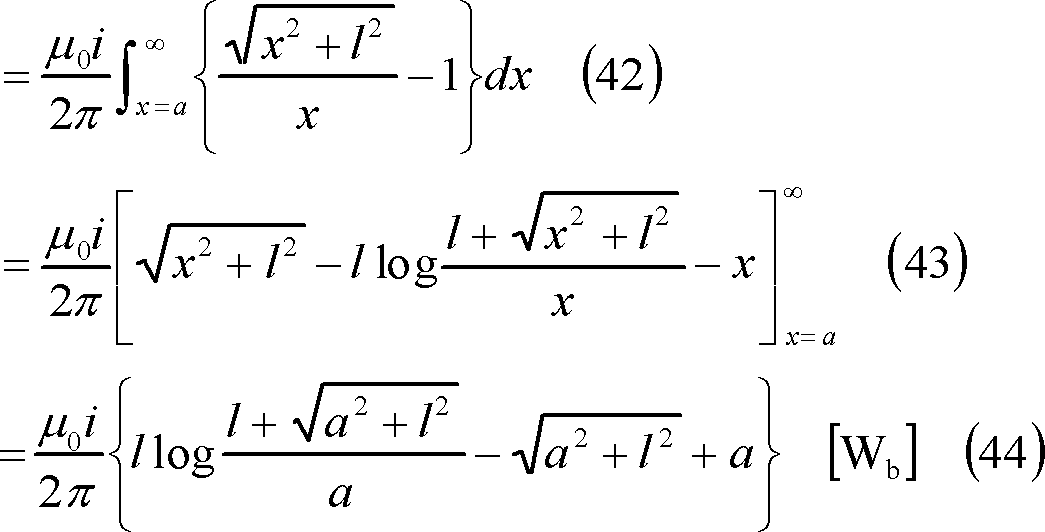
(39)式の注
(42)式の注(詳細は巻末資料を参照)
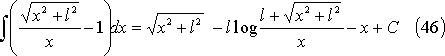
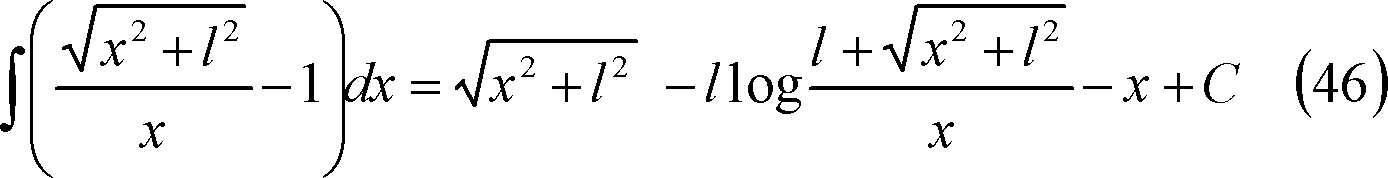
この結果、導体による自己インダクタンスLoは、
導体全体としての自己インダクタンスLは、
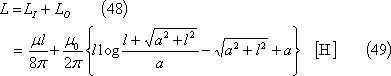
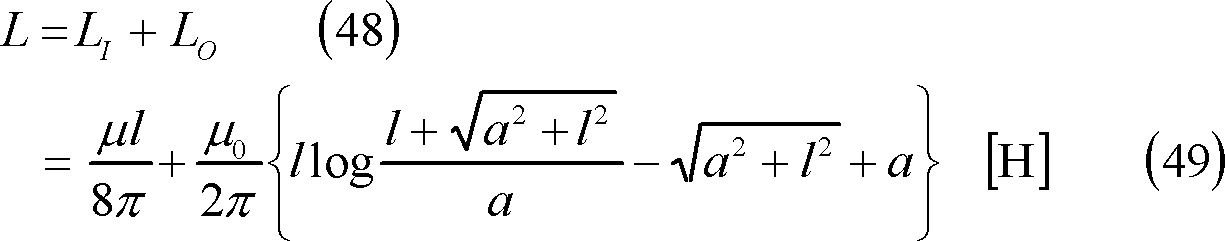
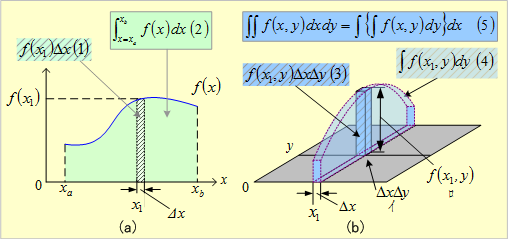
第12図 二重積分のしくみ
第13図(a)のように半径r[m]の直線導体が線間間隔D[m]で正三角形配置されている三相一回線線路がある。いま、 D>>rであり、各相に対称三相交流が流れている場合は、同図(b)において、各相導体より充分に遠い点Pまでの磁束は、次式のようになる。
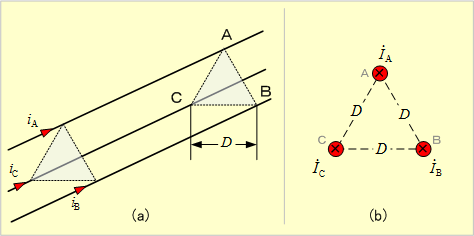
第13図 三相一回線路
A相電流
![]()
![]() がつくる磁束
がつくる磁束
![]()
![]() は、
は、
B相電流
![]()
![]() とC相電流
とC相電流
![]()
![]() がつくる磁束で、A相導体と鎖交する磁束
がつくる磁束で、A相導体と鎖交する磁束
![]()
![]() 、
、
![]()
![]() は、
は、
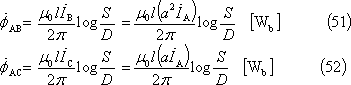
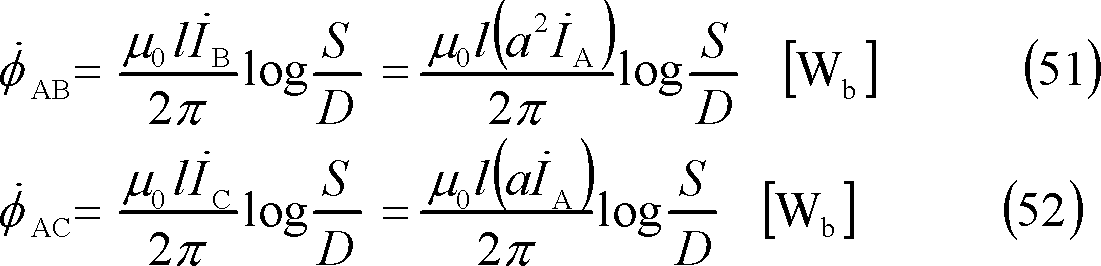
となり、A相導体と鎖交する総磁束
![]()
![]() は、
は、
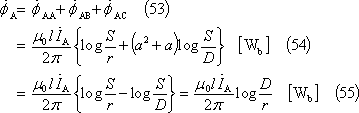
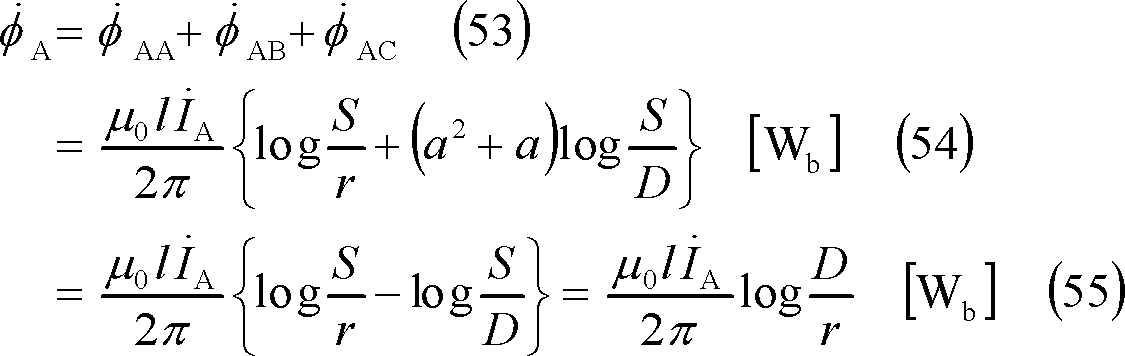
となるので、A相のインダクタンスは、次式となる。
この結果、導体内の自己インダクタンスを含めて考えると、各相のインダクタンスは次のようになる。
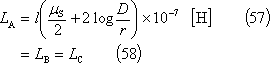
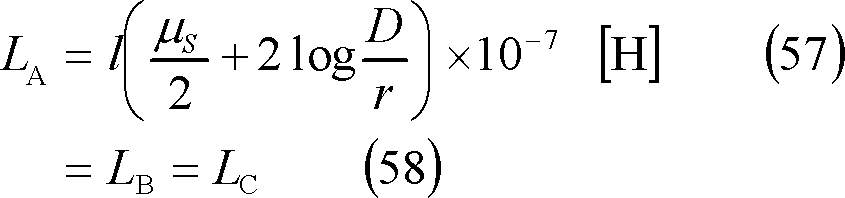
ここで、
![]()
![]() とすれば、線路1km当たりの各相のインダクタンスLは、
とすれば、線路1km当たりの各相のインダクタンスLは、
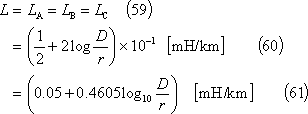
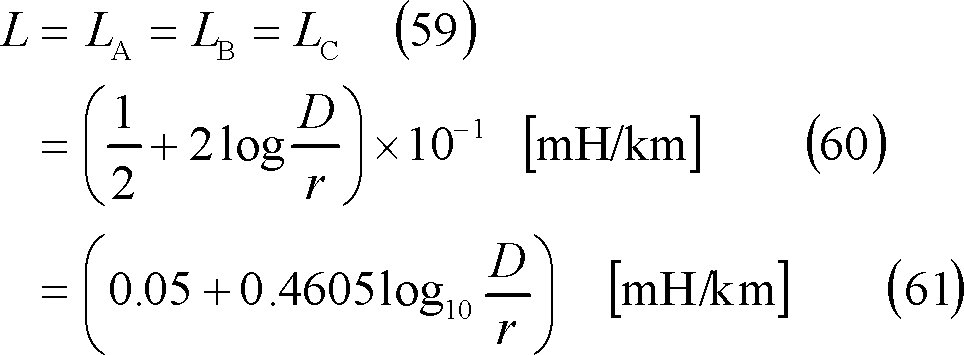
第14図のように、断面が円形(半径a [m])で、半径r [m]の環状導体の自己インダクタンスLはいくらになるか。ただし、導体の透磁率μ、導体内部を電流が均一に流れ、
![]()
![]() であるとする。
であるとする。
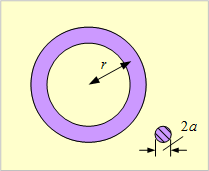
第14図 環状導体
内部インダクタンスLiは、断面積π a 2、長さ2π rの直線導体と見なせるので、
外部インダクタンスL0は、次式となる。(説明省略)
求める自己インダクタンスLは、
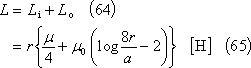
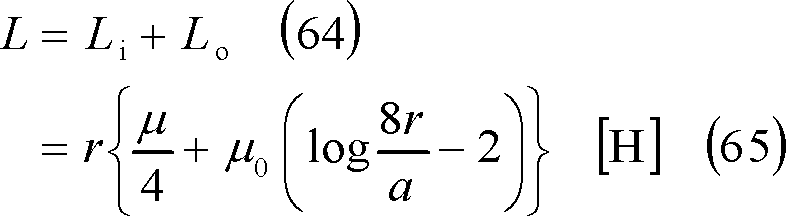
(1)環状ソレノイド
第15図のように、磁路の断面積S [m2]、平均磁路長l [m]、透磁率μの環状ソレノイドがあり、巻数が
![]()
![]() の2個のコイルが巻かれている。いま、相互誘導磁束が自己誘導磁束の80%であるとすれば、両コイル間の相互インダクタンスはいくらになるか。
の2個のコイルが巻かれている。いま、相互誘導磁束が自己誘導磁束の80%であるとすれば、両コイル間の相互インダクタンスはいくらになるか。
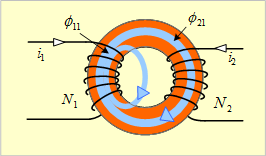
第15図
自己誘導磁束を
![]()
![]() 、相互誘導磁束を
、相互誘導磁束を
![]()
![]() とすれば、題意により、
とすれば、題意により、
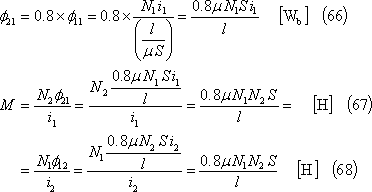
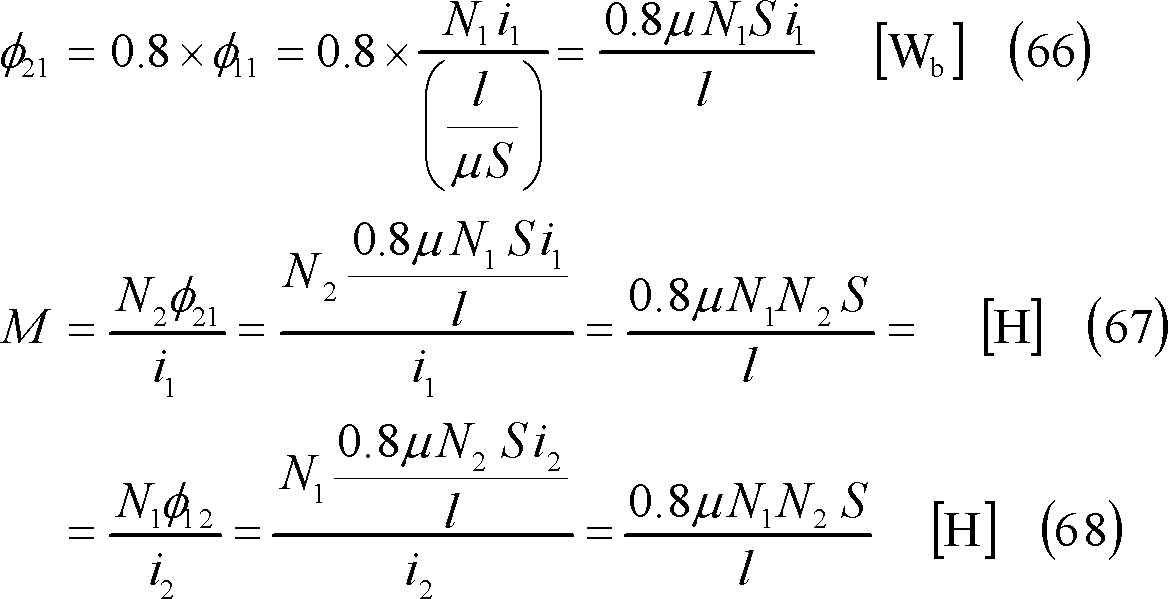
[参考] 自己インダクタンスと相互インダクタンスの関係
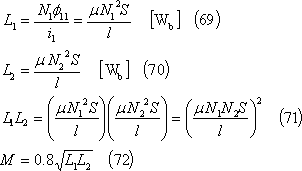
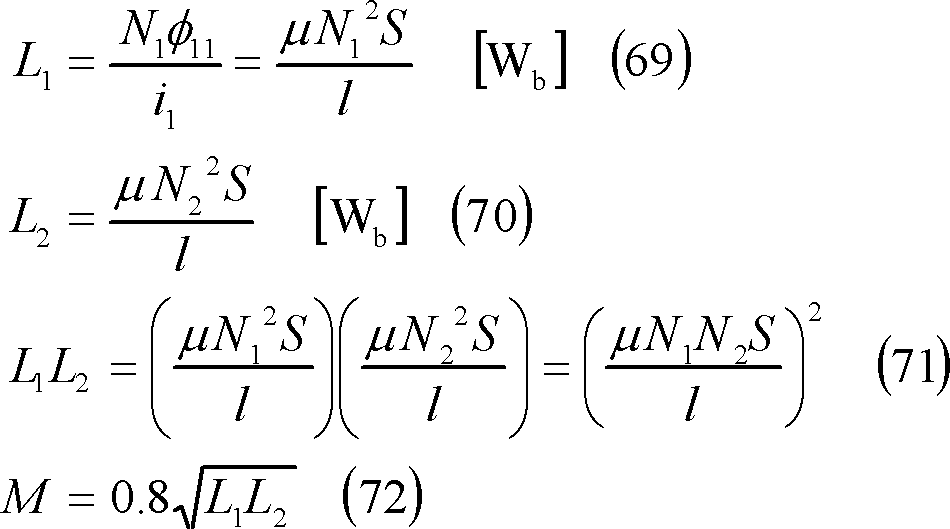
(2)円形コイル間
第16図のように、半径a(b)[m]、巻数NA(NB)の二つの円形コイルA(B)がある。いま、Aコイルの中心から軸上l[m]の点でAコイルの軸とθの傾きをもつBコイルがあるとき、両コイル間の相互インダクタンスはいくらになるか。ただし、
![]()
![]() >>
>>
![]()
![]() であるとする。
であるとする。
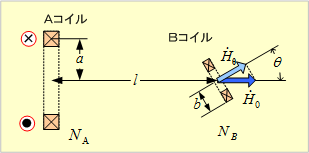
第16図 円形コイル間の相互インダクタンス
Aコイルを流れる電流iA[A]によって、Bコイル中心にできる磁界H0の磁束密度B0は、
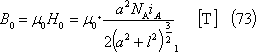
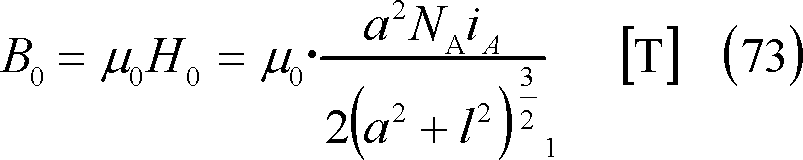
したがって、Aコイルのつくる磁束のうち、Bコイルと鎖交する相互磁束
![]()
![]() は、
は、
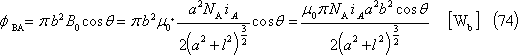
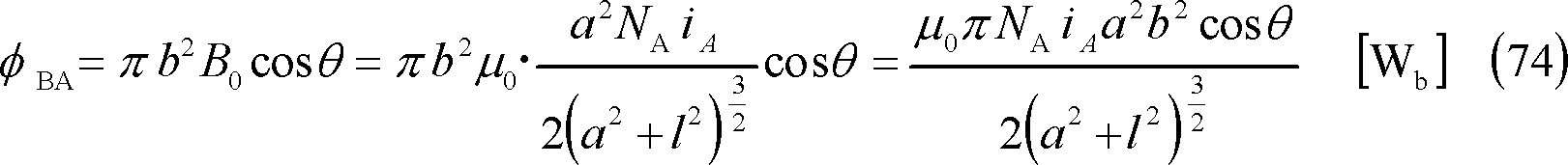
なので、求める相互インダクタンスは、
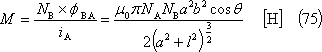
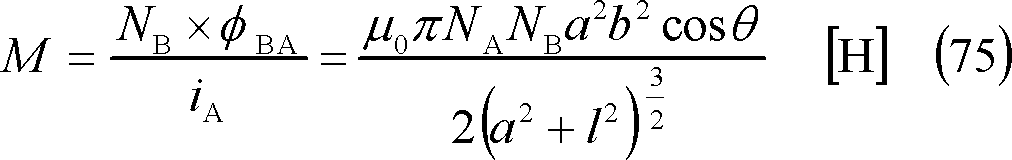
(3)平行導体間
第17図のような、直線導体が間隔
![]()
![]() で平行に張られているとき、長さ
で平行に張られているとき、長さ
![]()
![]() の部分の両線間の相互インダクタンスはいくらか。ただし、導体の太さは無視するものとする。
の部分の両線間の相互インダクタンスはいくらか。ただし、導体の太さは無視するものとする。
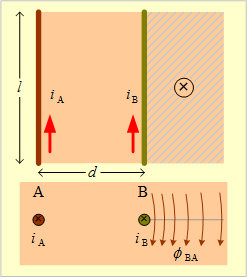
第17図 平行導体間の相互インダクタンス
第17図において、導体Aのつくる磁束のうち導体Bと鎖交する磁束
![]()
![]() (相互誘導磁束)は、図のようになるから、単独の直線導体のつくる磁束の計算で、Aからd[m]以上離れた磁束に等しいので、(42)式の磁束計算で積分の下限値をdとした次式で計算すればよいことになる。
(相互誘導磁束)は、図のようになるから、単独の直線導体のつくる磁束の計算で、Aからd[m]以上離れた磁束に等しいので、(42)式の磁束計算で積分の下限値をdとした次式で計算すればよいことになる。
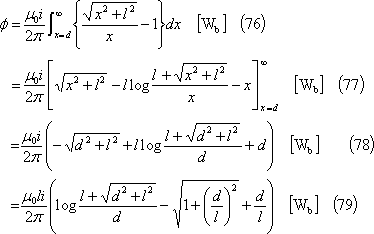
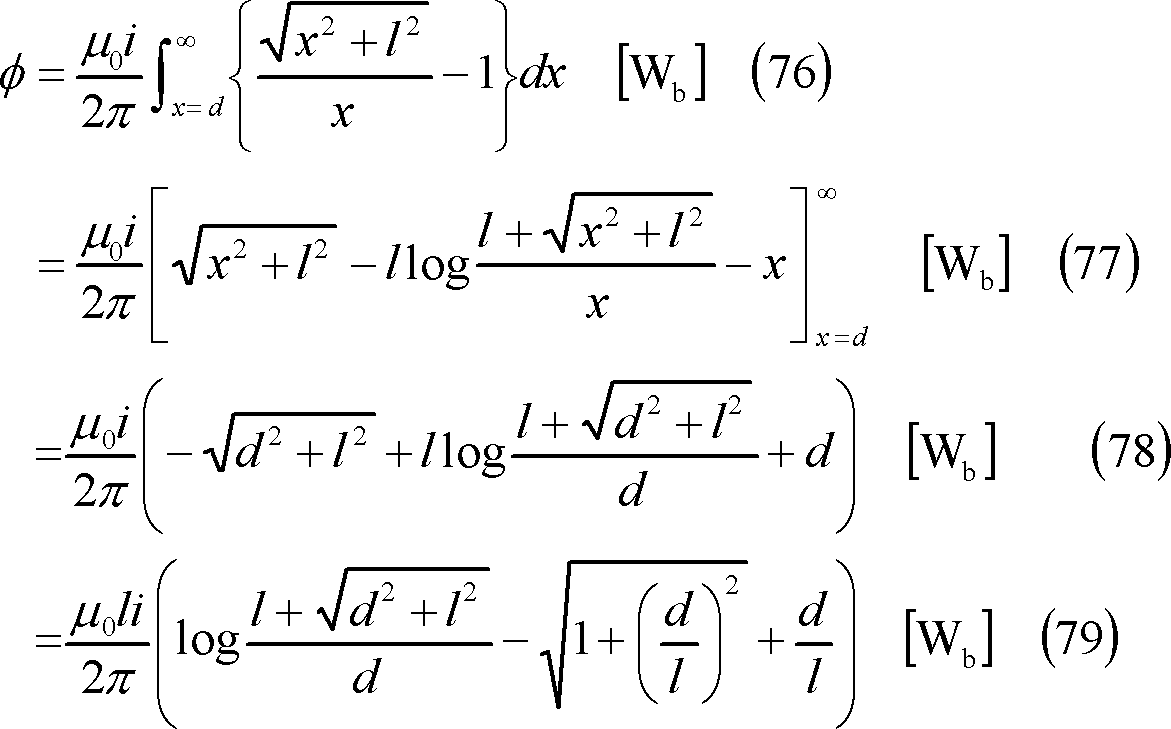
この結果、求める相互インダクタンスMは、次式となる。
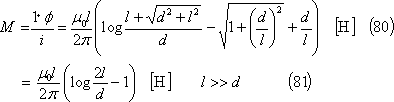
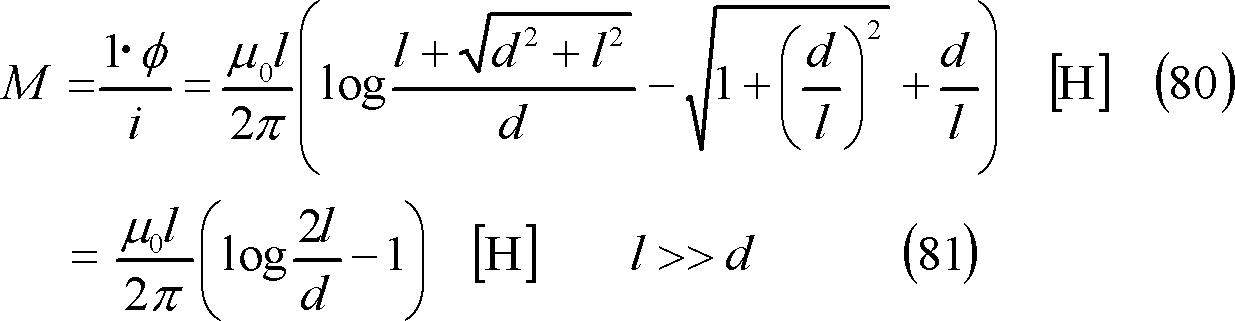
なお、図のように電流が同方向の場合は相互誘導磁束が自己誘導磁束と同方向となるので和動的、電流の方向が異方向の場合は相互誘導磁束が反対方向となるので差動的、の電磁気的な結合関係となる。
[1]自己インダクタンスの求め方・・・・・・第1図
[2]自己インダクタンス
環状ソレノイド・・・・・・・・・・・・・第2図、(8)、(9)式
無限長円筒ソレノイド・・・・・・・・・・第3図、(11)式
無限長直線導体による往復線路・・・・・・第4図、第5図、(16)式
直線導体の内部・・・・・・・・・・・・・第6図、第7図、(21)、(23)式
大地帰路の直線導体線路・・・・・・・・・第8図、第9図、(34)式
直線導体・・・・・・・・・・・・・・・第10図、第11図、第12図(47)(49)式
三相一回線路・・・・・・・・・・・・・・第13図、(57)、(60)、(61)式
環状導体・・・・・・・・・・・・・・・・第14図、(63)、(65)式
[3]相互インダクタンス
(1)環状ソレノイド・・・・・・・・・・・・・第15図、(67)、(68)式
(2)円形コイル間・・・・・・・・・・・・・・第16図、(75)式
(3)平行導体間・・・・・・・・・・・・・・・第17図、(80)、(81)式
終わり
(38)式の注
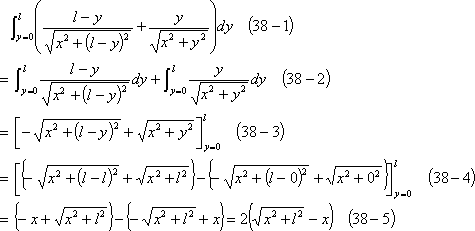
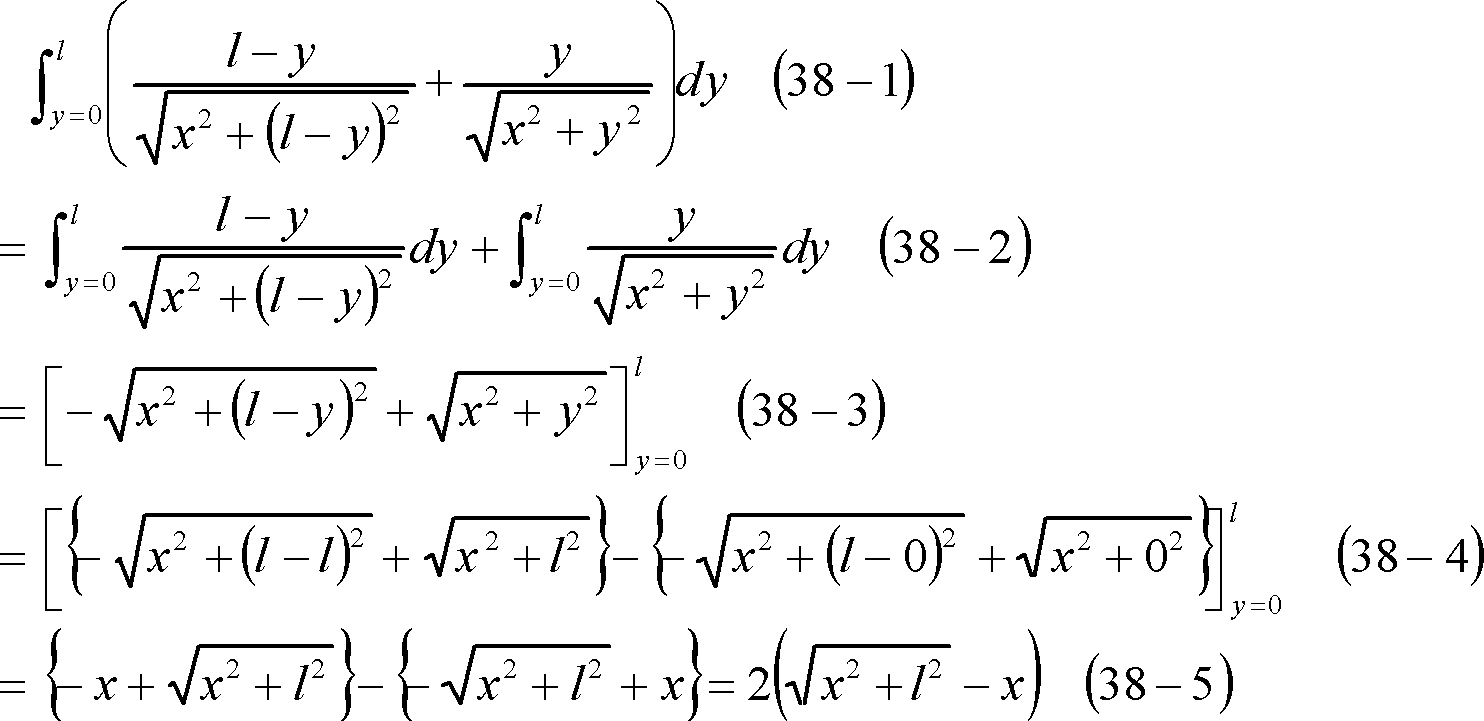
(42)式の注