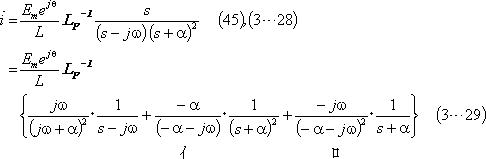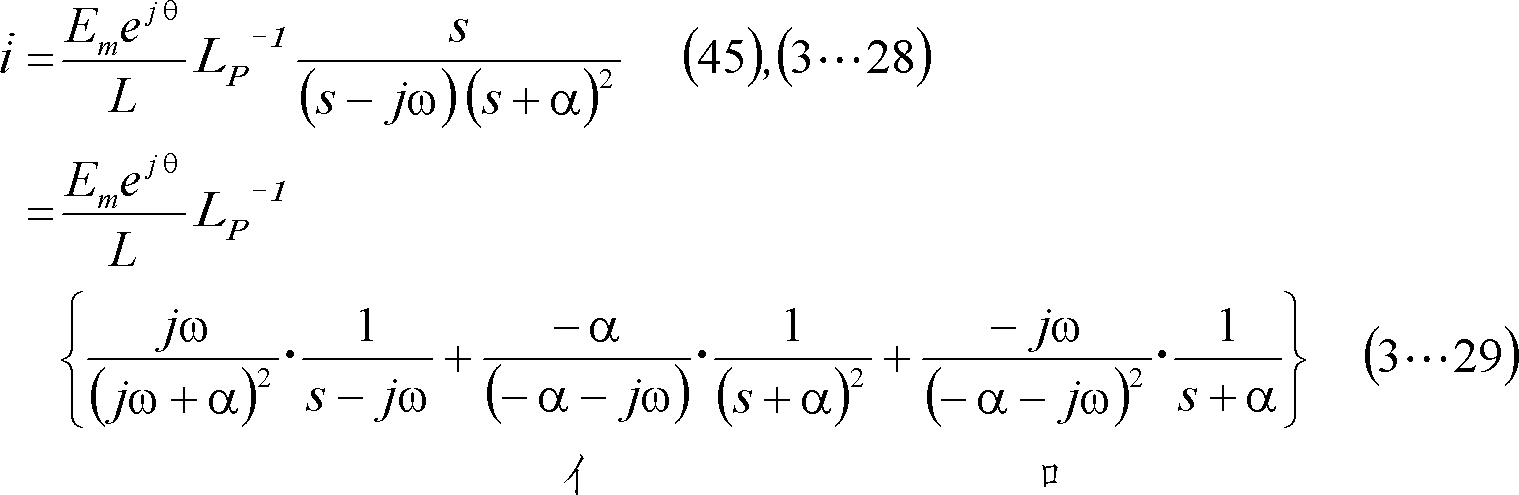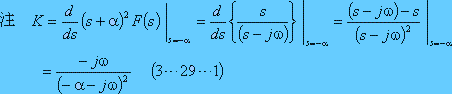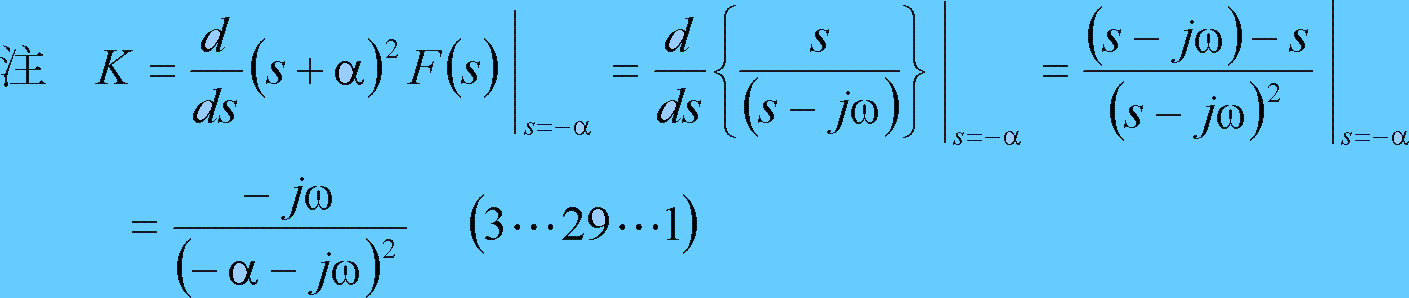〜終わり〜
■ぜひアンケートにご協力下さい■


電磁気現象は微分方程式で表され、一般的には微分方程式を解くための数学的に高度の知識が要求される。ラプラス変換は、計算手順さえ覚えれば、代数計算と変換公式の適用により微分方程式が解ける数学知識への負担が少ない解法である。このシリーズでは電気回路の過渡現象や制御工学等の分野での使用を念頭に置いて範囲を限定して、ラプラス変換を用いて解く方法を解説する。今回は、ラプラス変換等価回路について解説する。
1 電源、電流、回路定数をラプラス変換してs関数に直して(s記号式表示)、s回路をつくる。
2 s回路より求めたい量のs関数X(s)を求める。(s回路計算)
3 X(s)をラプラス逆変換して、求めたい量のt関数x(t)を算出する。(逆変換)
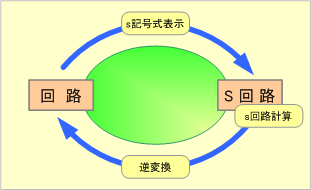
第1図 s記号式計算法の計算の流れ
【例題1】 第2図の交流回路が定常状態にある時、t=0の時、スイッチSを閉じてR2を短絡した場合、回路にはどんな電流が流れるか求めよ。
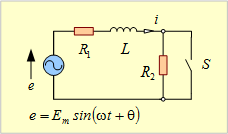
第2図
【解答】 この問題のs回路は、Sが投入された回路、つまりR2が短絡された状態の回路で、第3図となる。
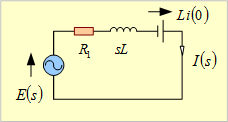
第3図 s回路
同図において、i(0)はR2が短絡される直前にLを流れている電流で、
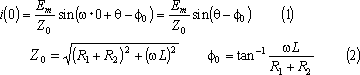
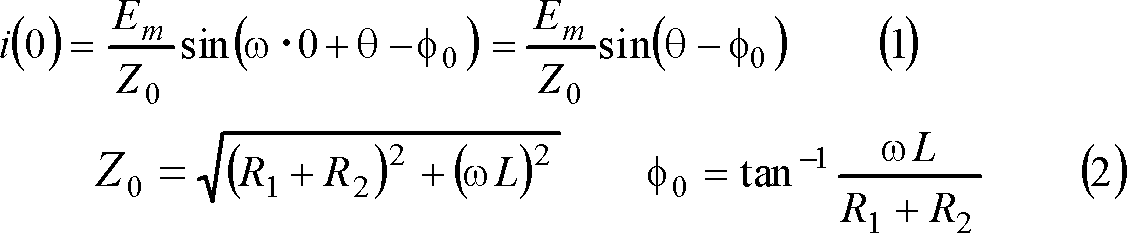
となる。電流I(s)は、
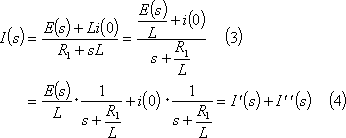
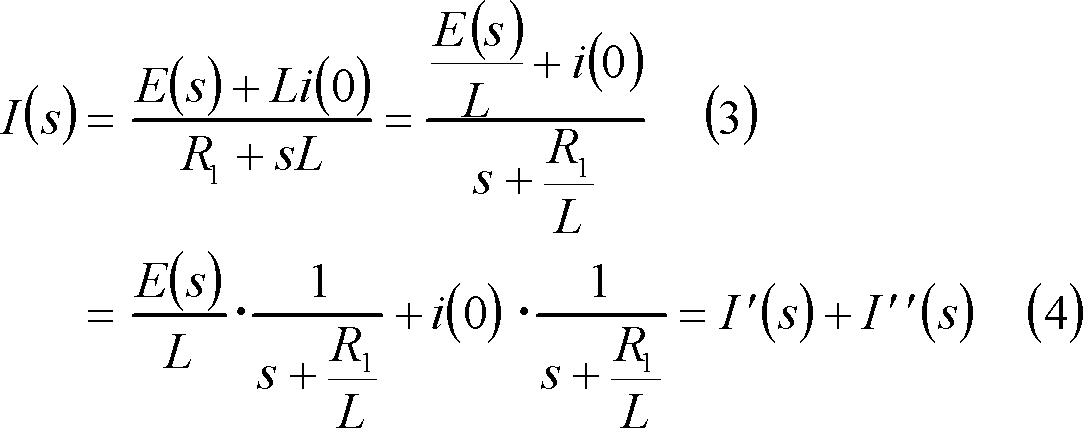
上式の第1項は、複素起電力法によれば、
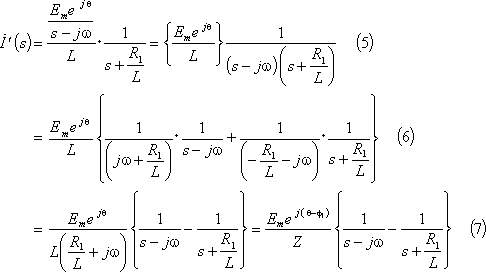
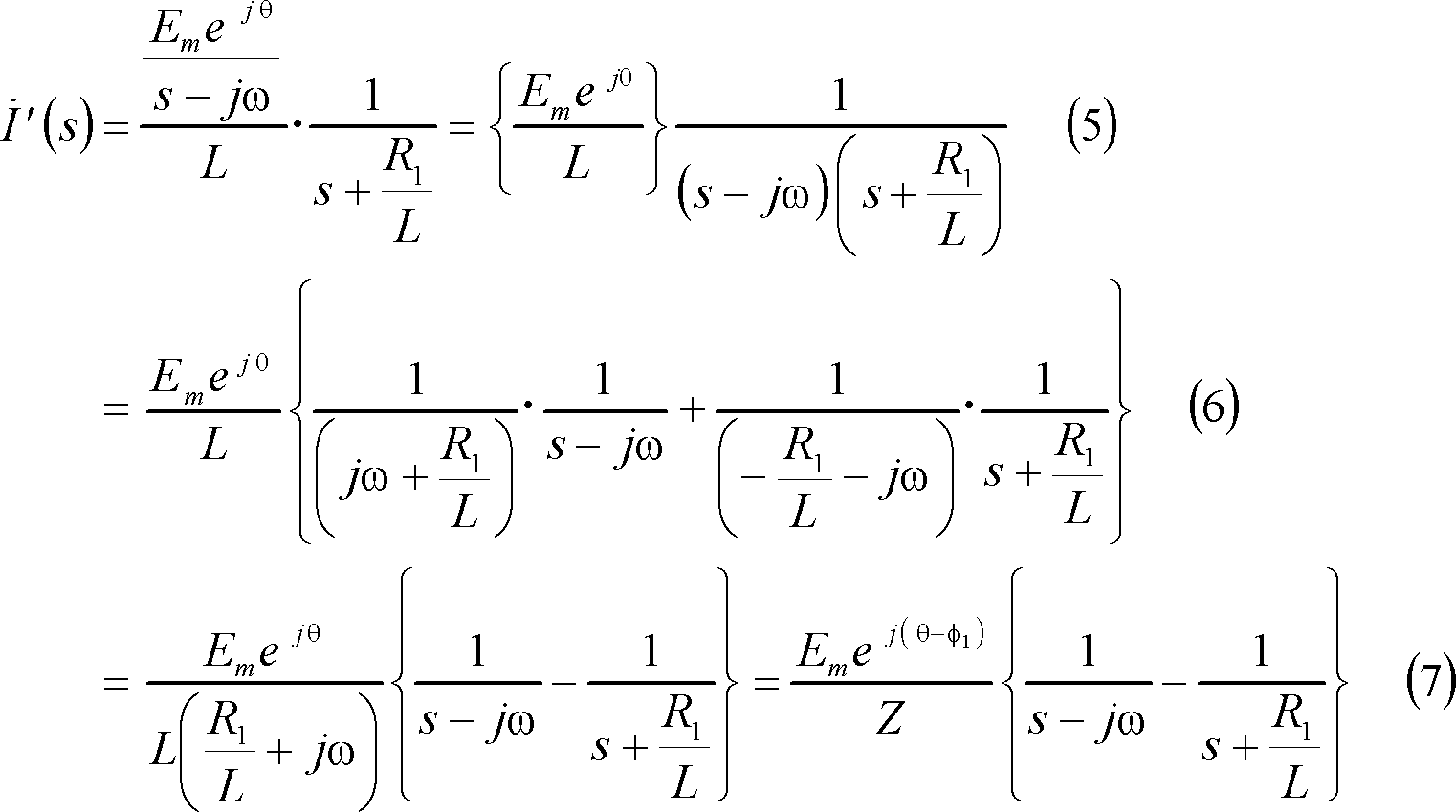
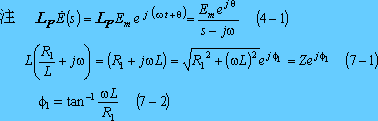
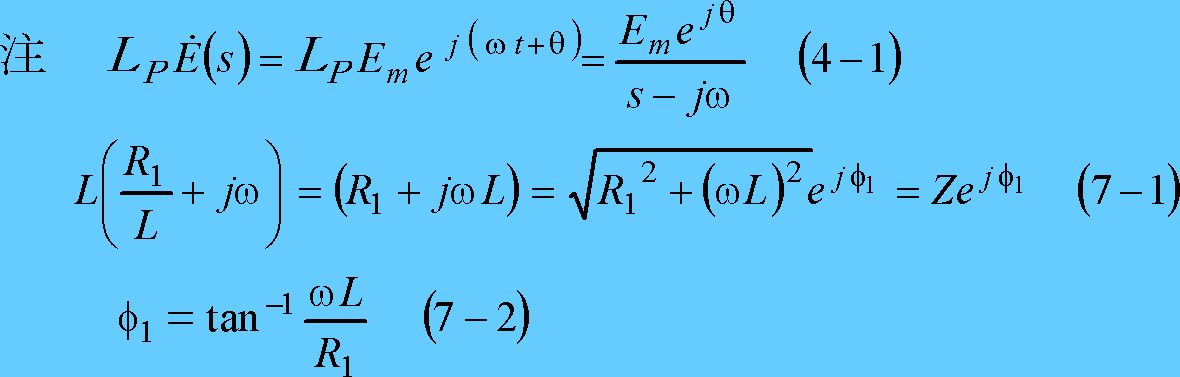
(7)式を次のように逆変換して、その虚数部を採れば、電流
![]()
![]() が求まる。
が求まる。
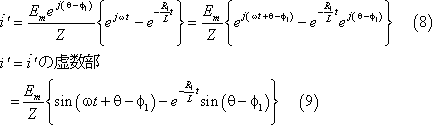
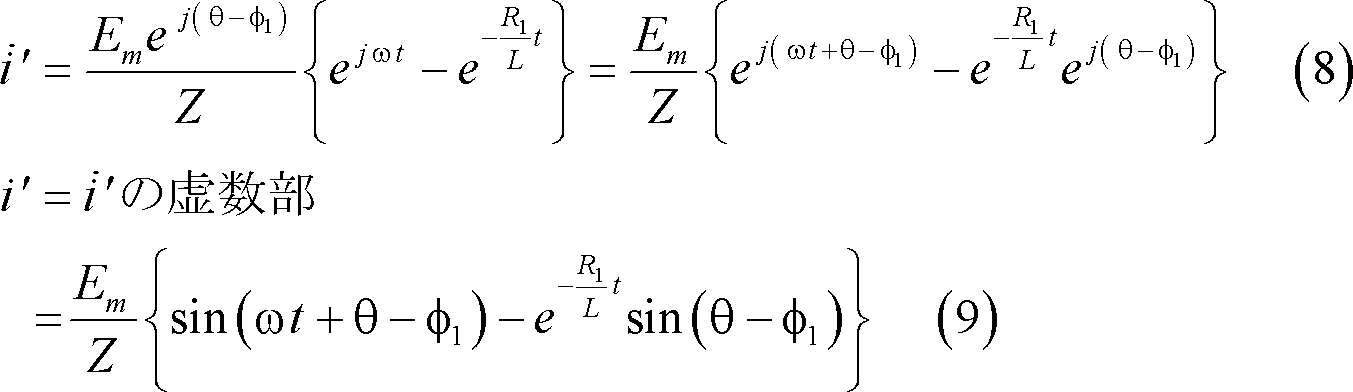
次に、(4)式第2項の電流
![]()
![]() は、
は、
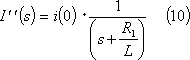
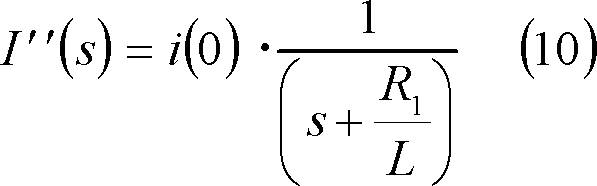
なので、電流
![]()
![]() は、上式を逆変換して、
は、上式を逆変換して、
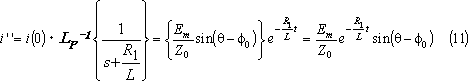
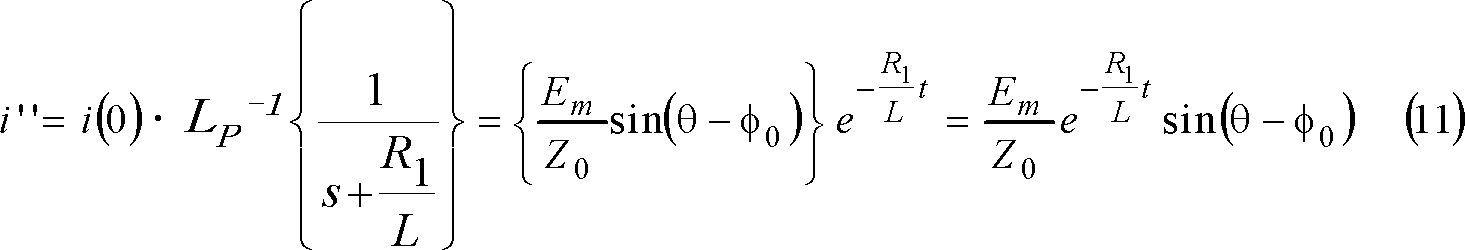
求める電流は、
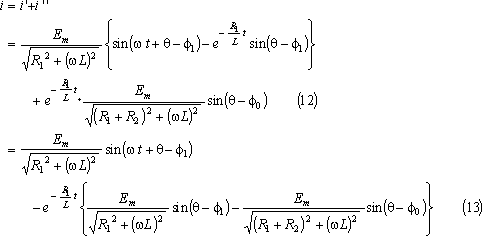
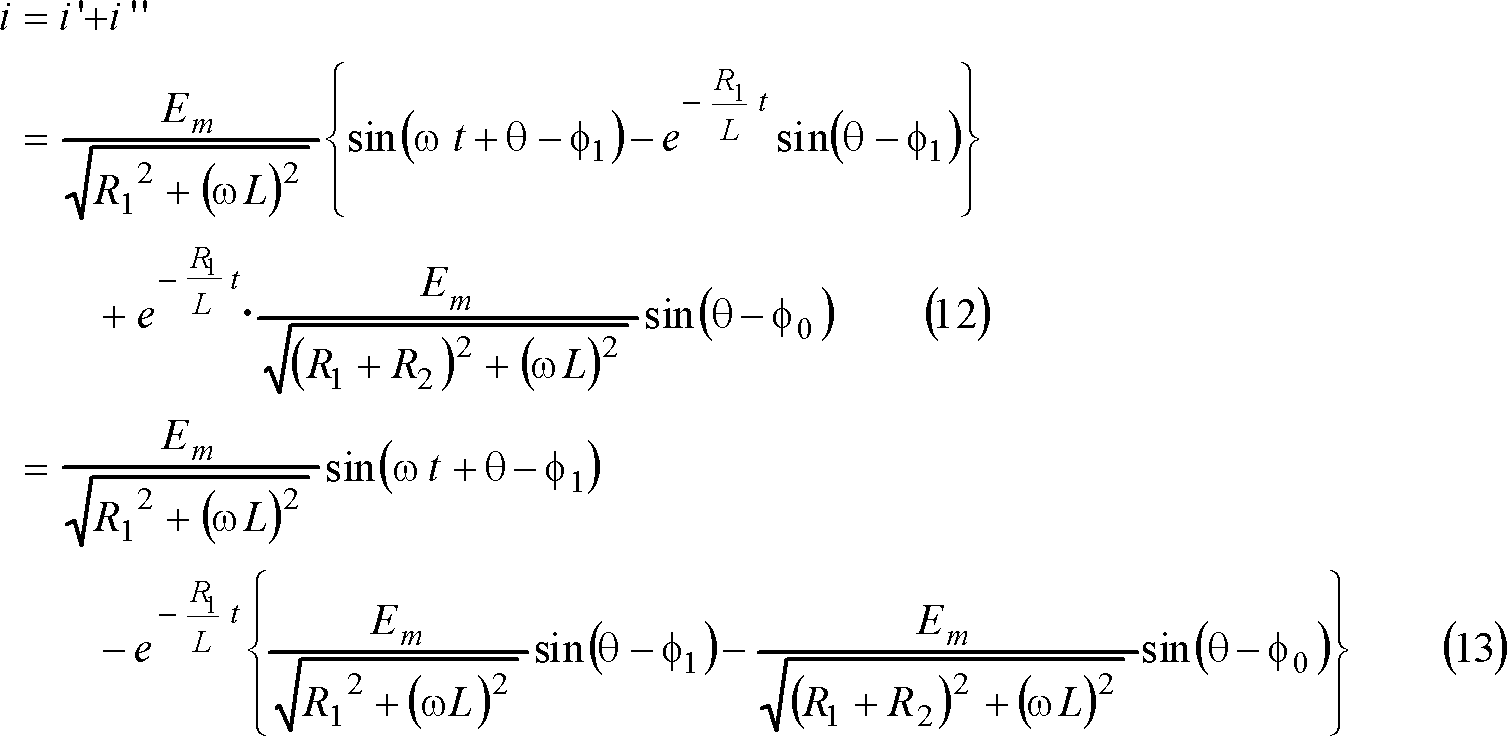
電流
![]()
![]() のグラフは第4図となる。
のグラフは第4図となる。
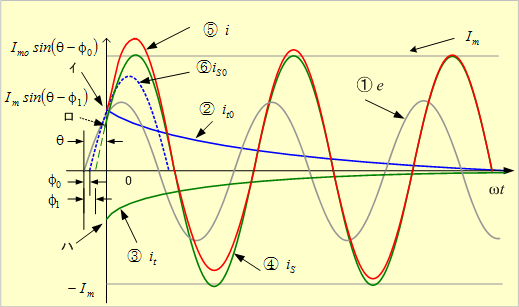
第4図 電流
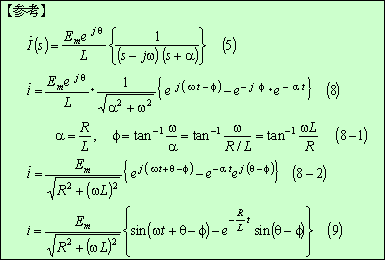
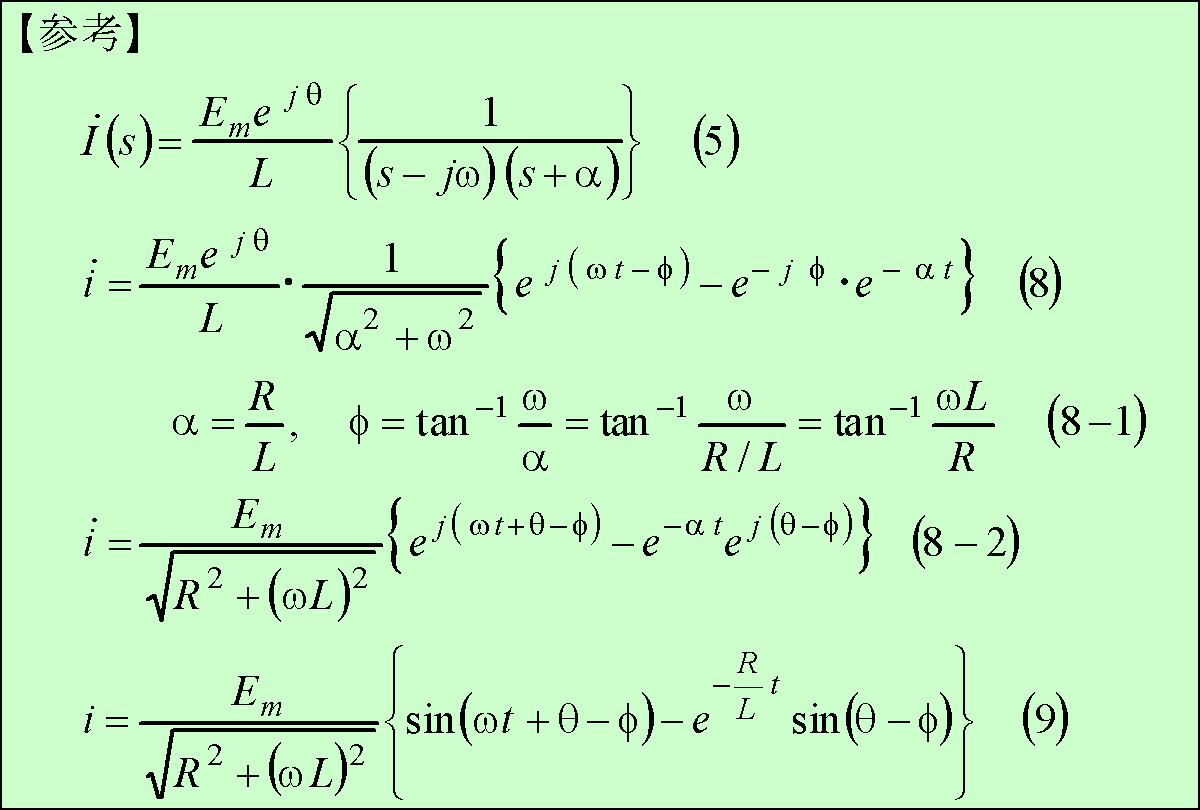
【例題2】 第5図の回路が定常状態にあるとき、t=0でSを閉じた時、Lに流れる電流を求めよ。
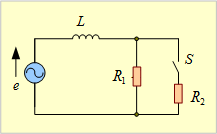
第5図
【解答】 この場合のs回路は、第5図の回路でSを閉じた状態の第6図となる。
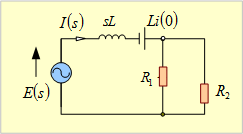
第6図 s回路
同図において、i(0)はSを閉じる直前にLを流れていた電流なので、
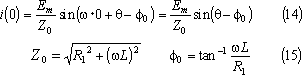
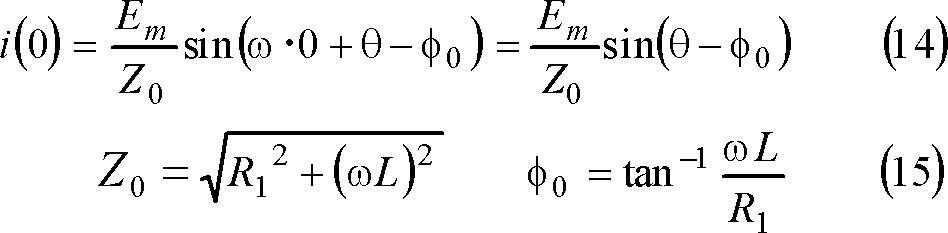
S投入後、Lを流れる電流
![]()
![]() は、s回路により次式が成立する。
は、s回路により次式が成立する。
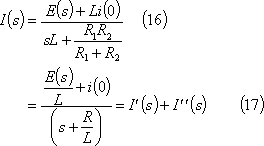
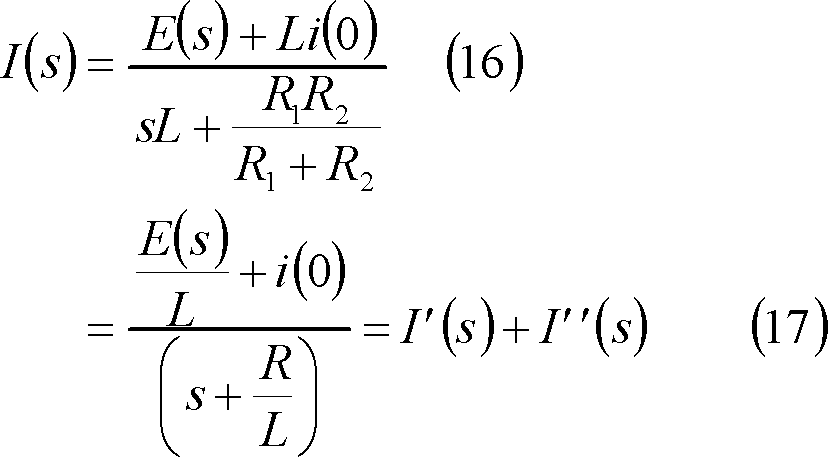
ここで、
と置く。(17)式第1項の電流
![]()
![]() は、複素起電力法によれば、
は、複素起電力法によれば、
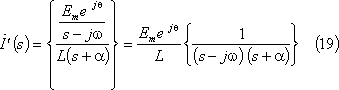
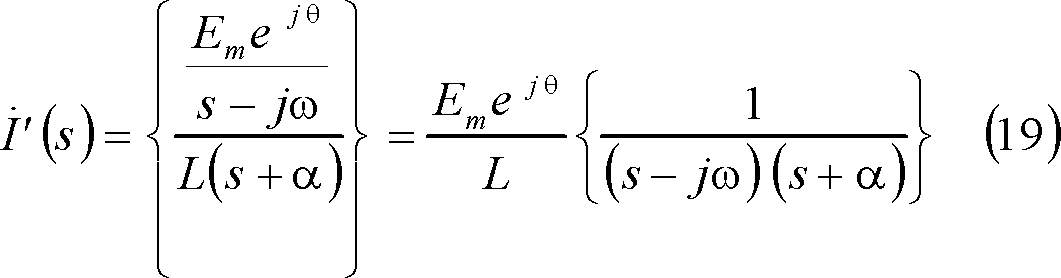
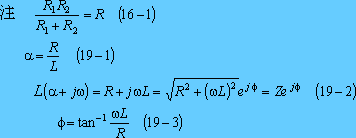
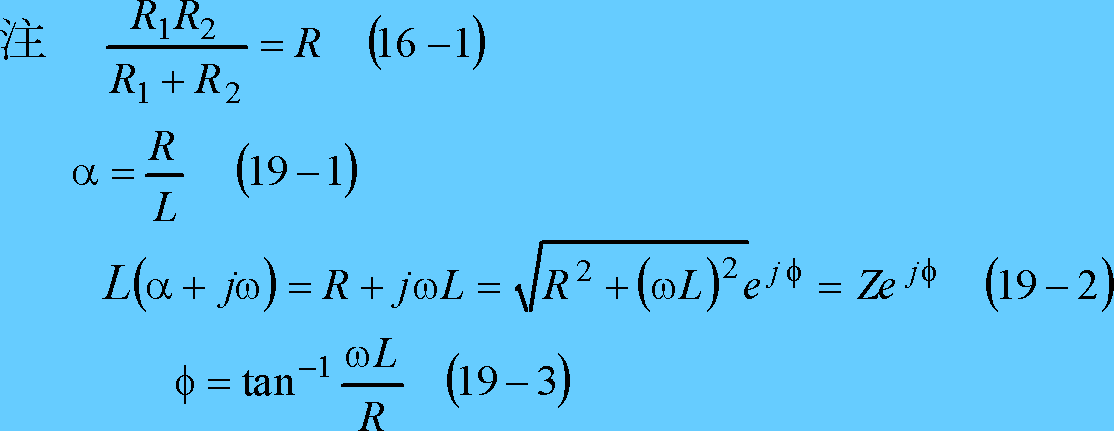
であり、この計算は第4図下の【参考】の結果から、電流は次式となる。
一方、(17)式第2項の電流
![]()
![]() は、
は、
求める電流は次式となる。
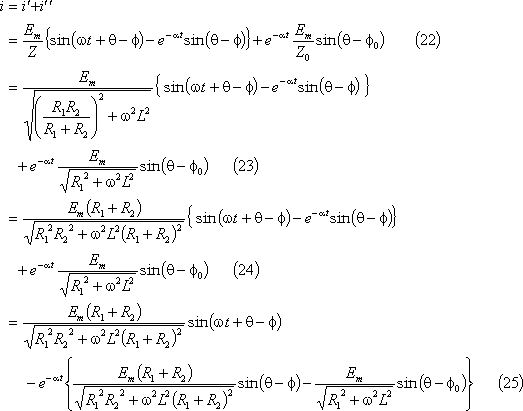
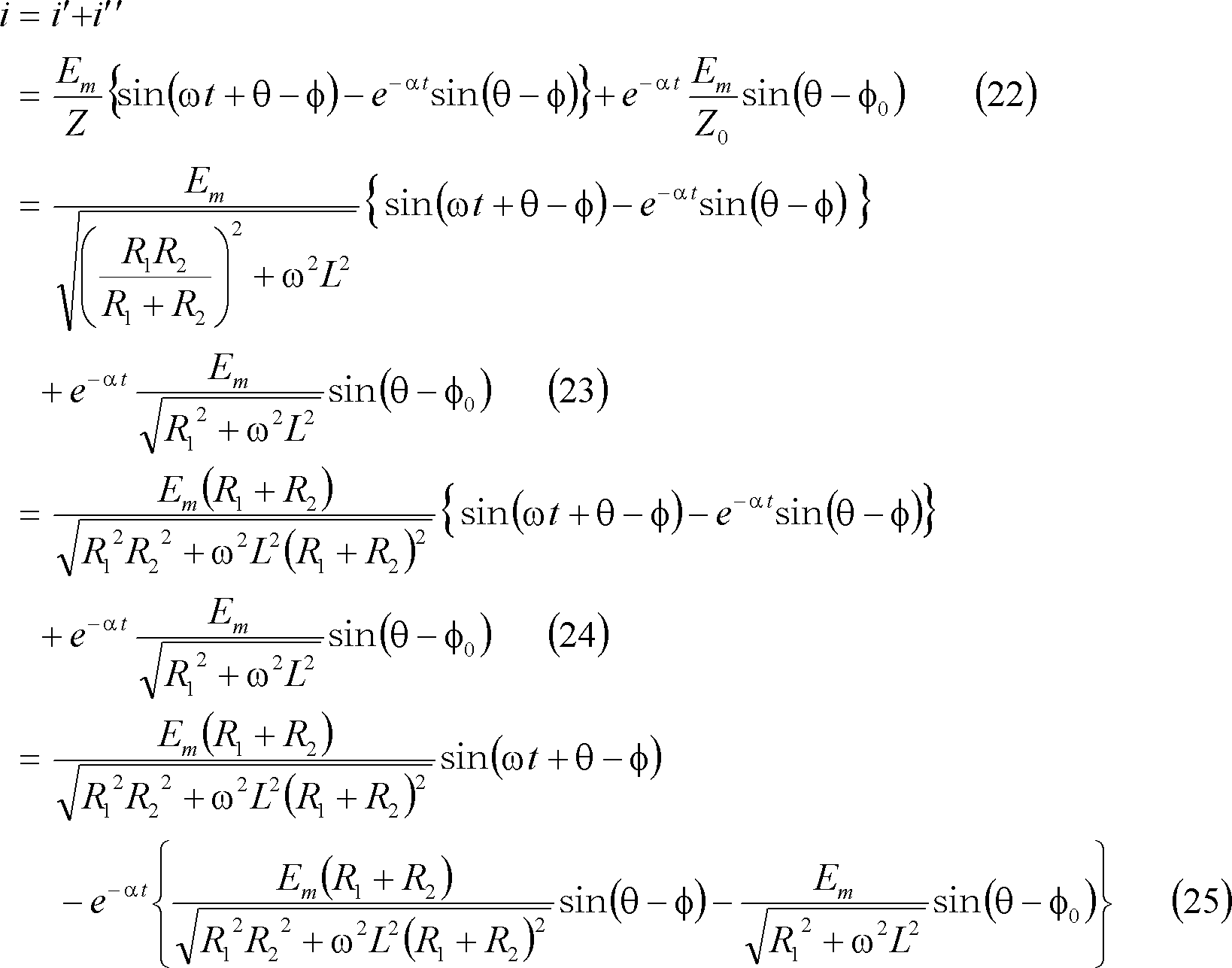
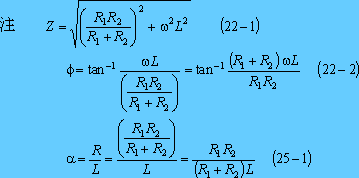
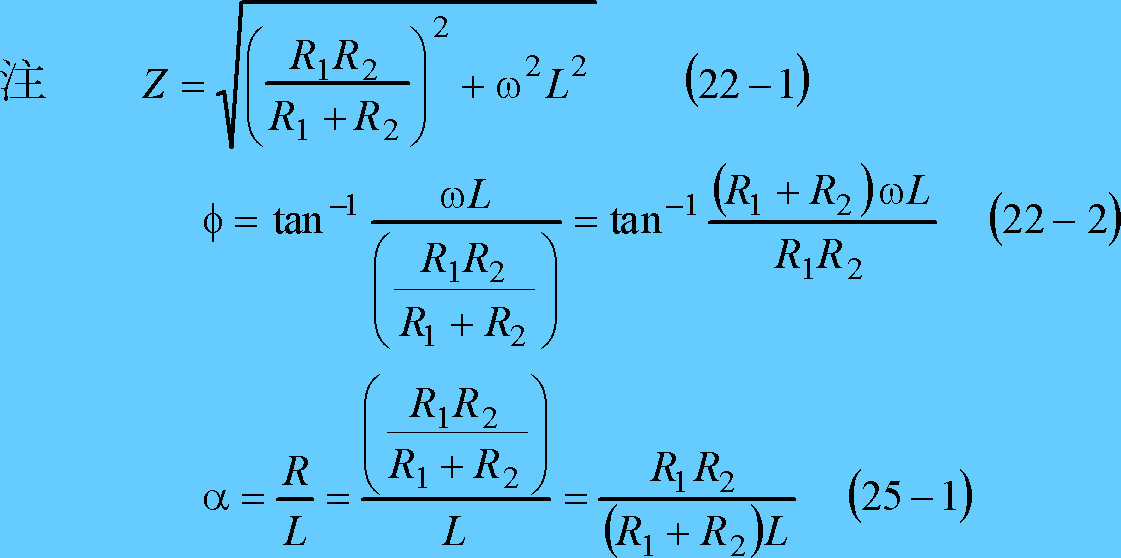
第7図に電流のグラフを示す。
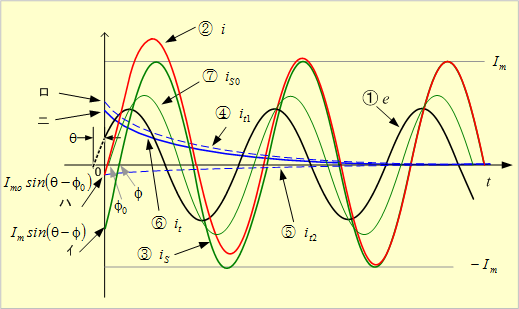
第7図 電流
【例題3】 第8図の回路において、t=0でSを閉じて進相負荷を接続したとき回路にはどんな電流が流れるか。ただし、CにはS投入前、電荷はなかったものとする。
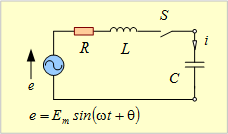
第8図
【解答】 この場合のs回路は第9図となる。
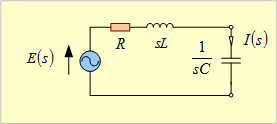
第9図 s回路
複素起電力法によれば、
![]()
![]()
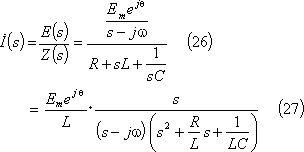
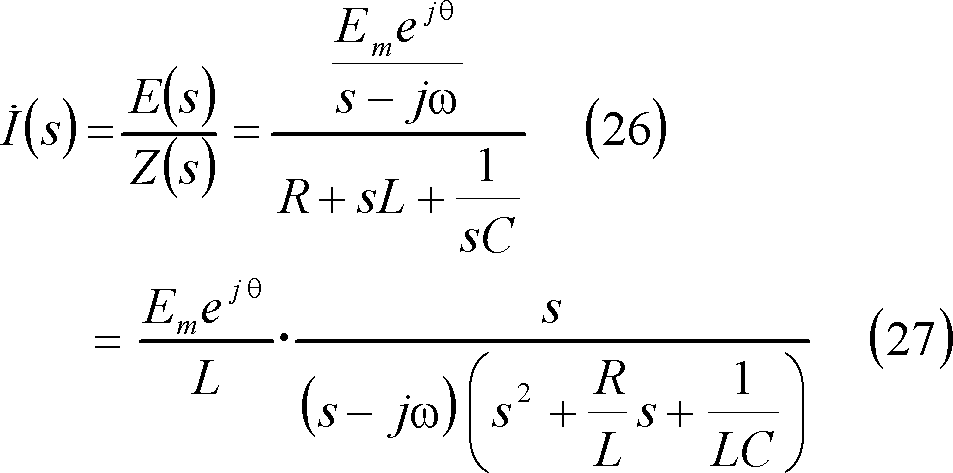
上式s関数部の分母にあるsの二次式は、
となり、RLCの大小関係によって、
の3ケースがある。ここで、
とおく。
①
![]()
![]() の場合
の場合
とおけば、(28)式は、
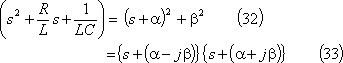
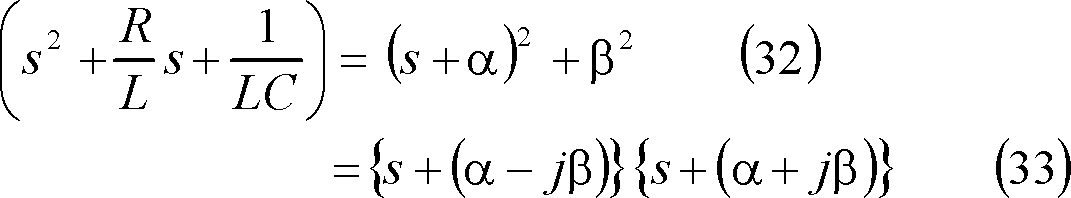
と変形できるので、(27)式の
![]()
![]() は、
は、
となる。したがって、巻末の参考計算[3−1]により、複素電流
![]()
![]() と電流
と電流
![]()
![]() は次の各式となる。
は次の各式となる。
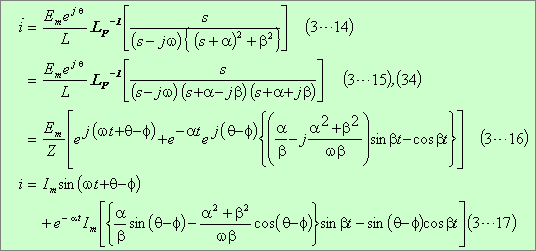
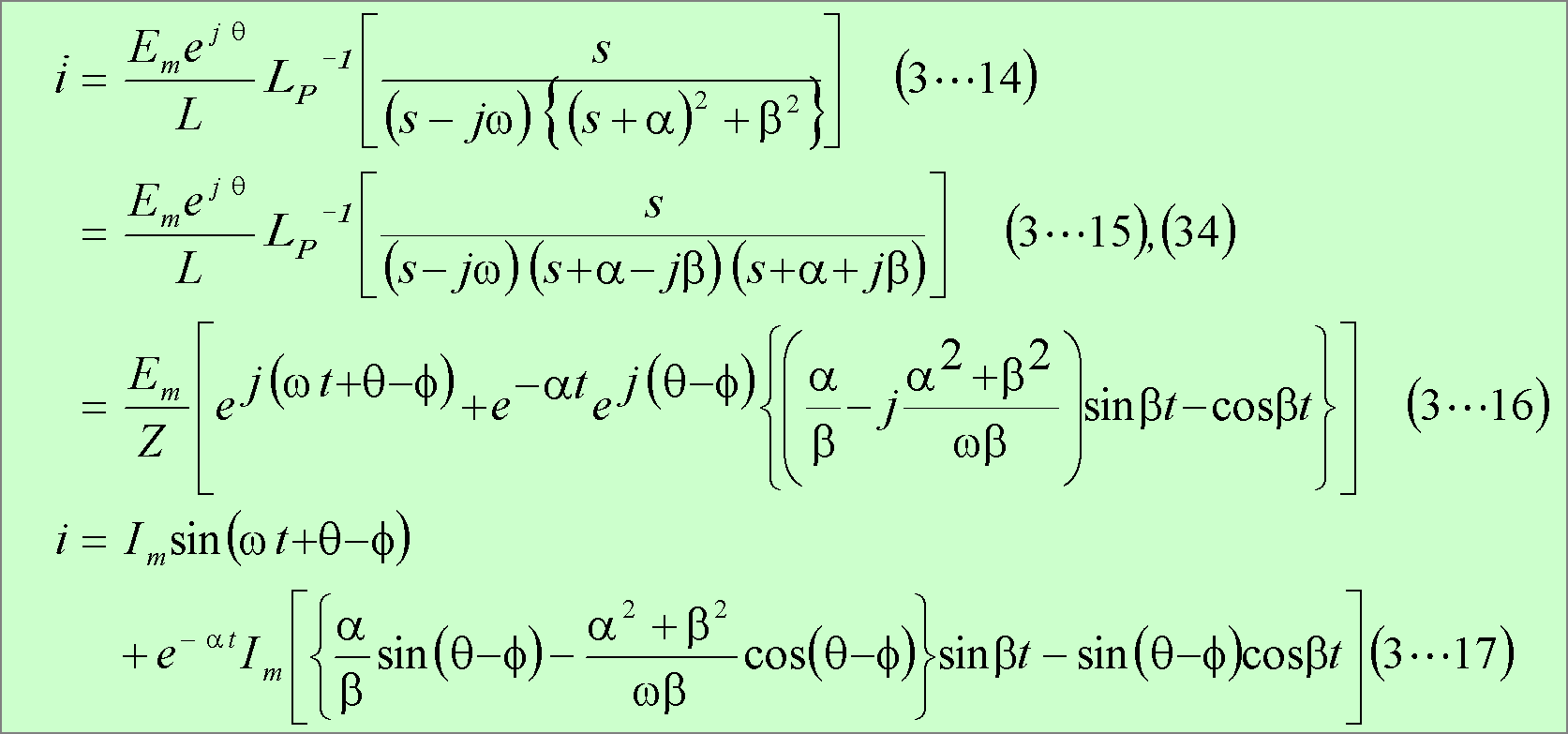
この結果、求める電流は次式となる。
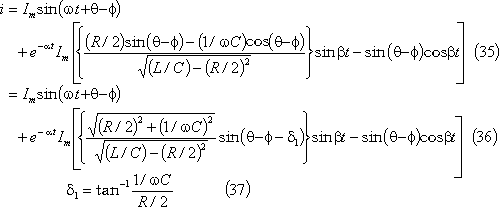
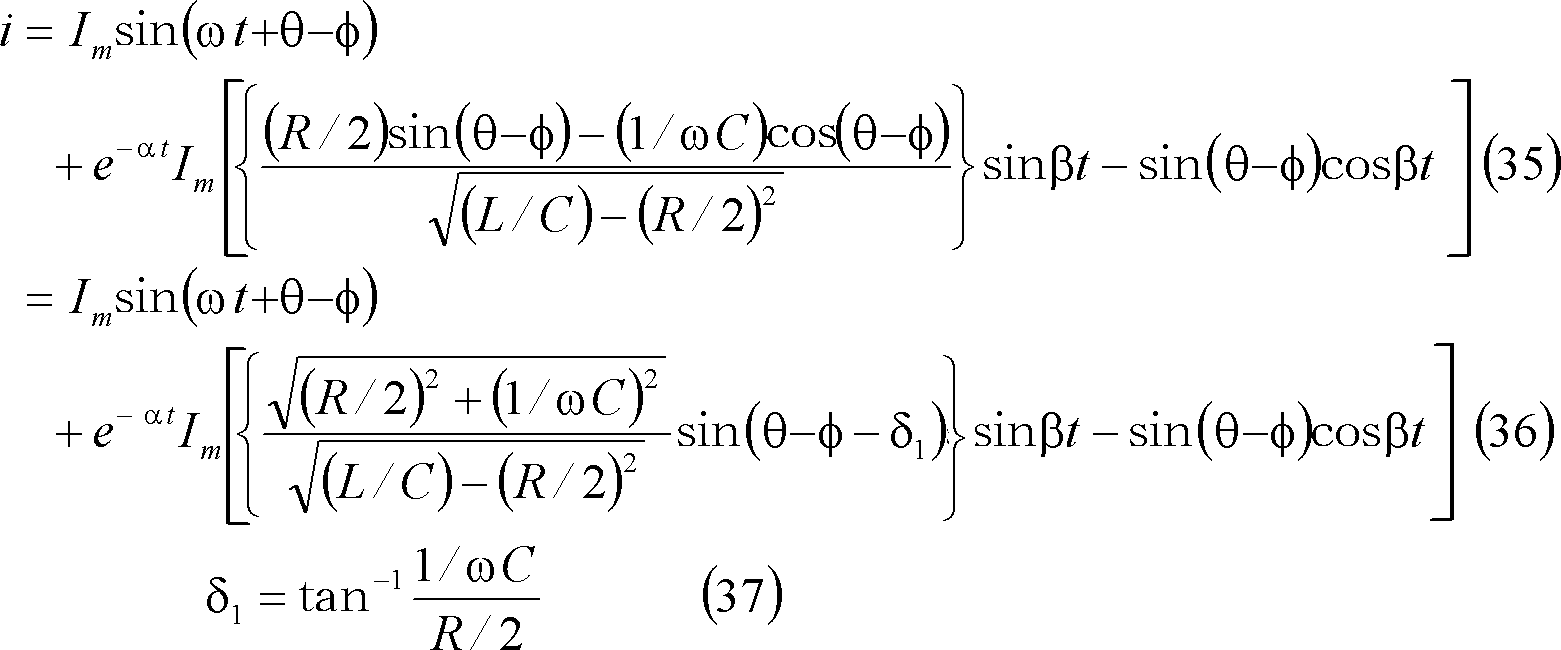
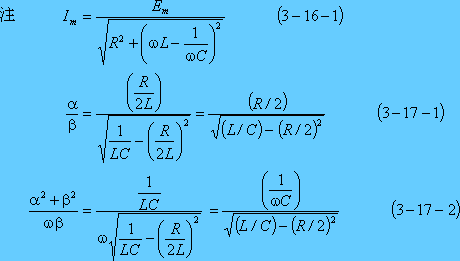
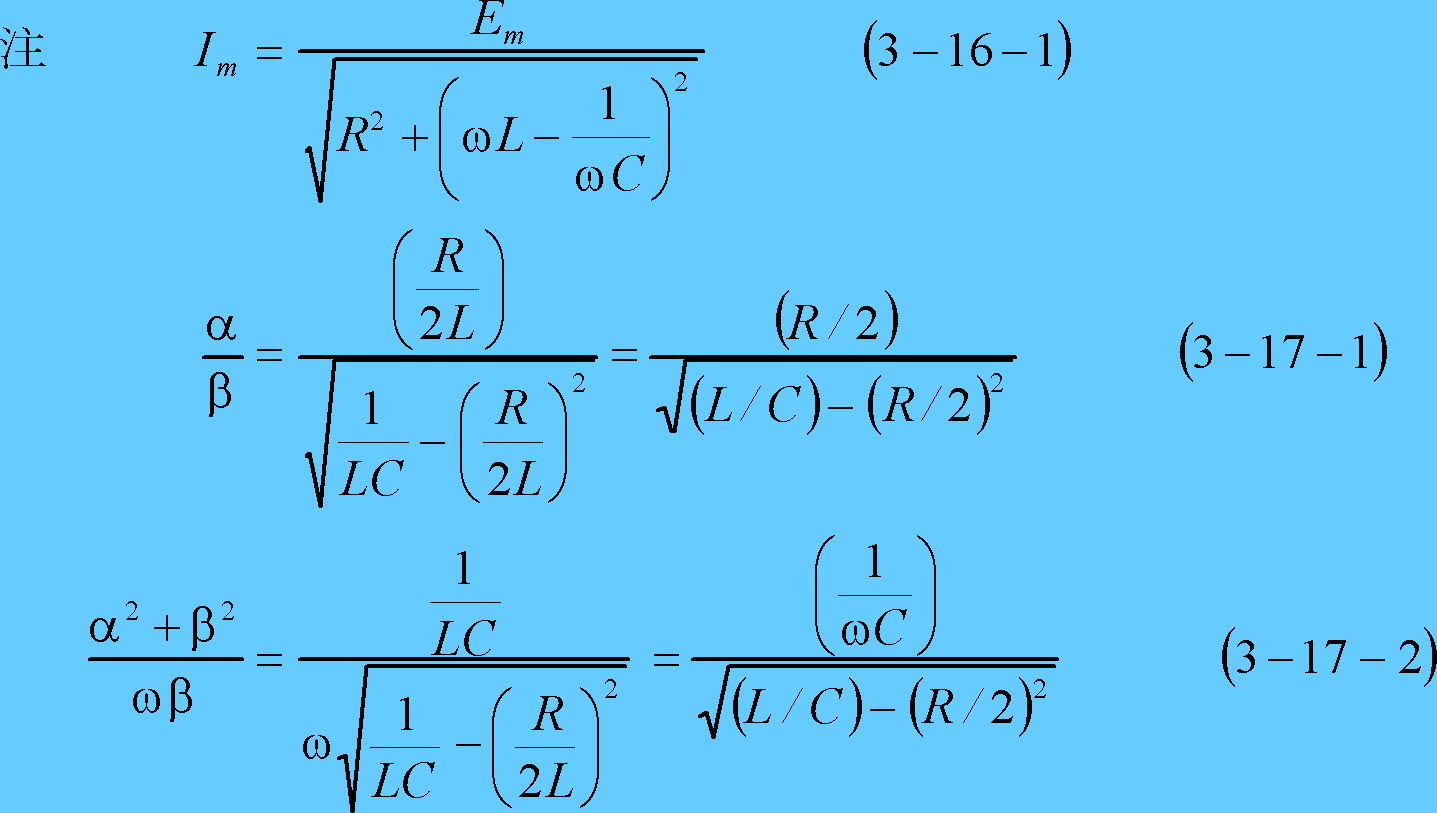
第10図にこの場合の電流波形を示す。
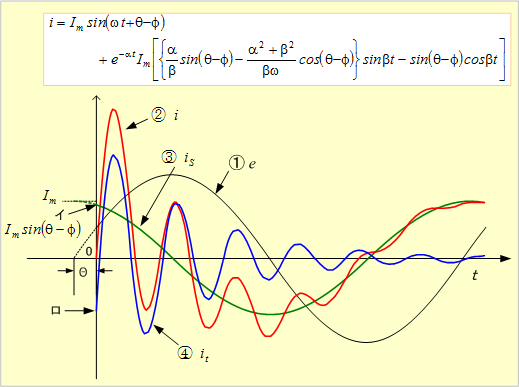
第10図 β>0(振動形)の場合の電流波形
②
![]()
![]() の場合
の場合
とおけば、
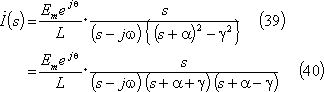
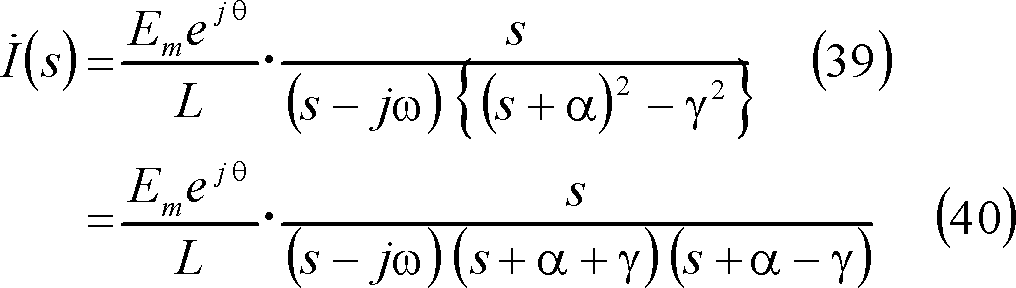
となる。この式はβ>0の場合の
![]()
![]() である(34)式において、
である(34)式において、
![]()
![]() を
を
![]()
![]() に置き換えれば
に置き換えれば
![]()
![]() 、(40)式が作れるので、複素電流の式もβ>0の場合の(3…16)式で
、(40)式が作れるので、複素電流の式もβ>0の場合の(3…16)式で
![]()
![]() とおけば求められ、巻末の参考計算[3−2]によって次式となる。
とおけば求められ、巻末の参考計算[3−2]によって次式となる。
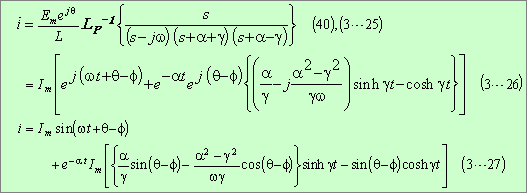
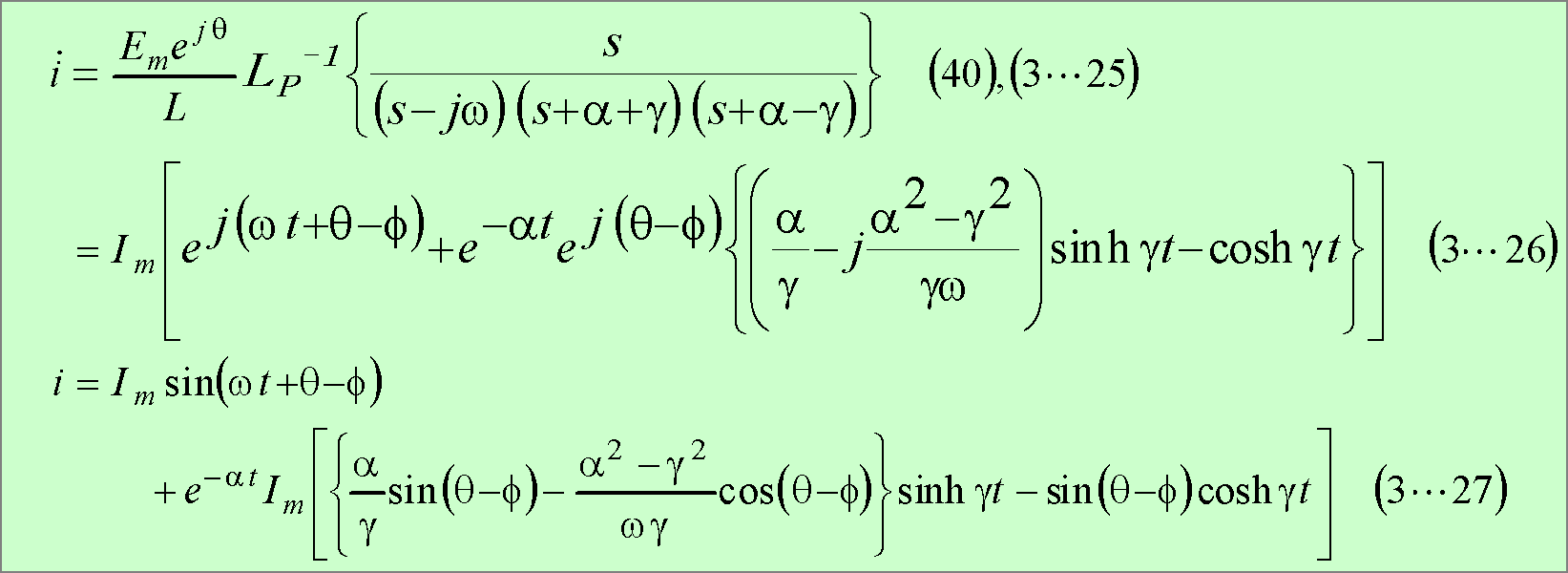
したがって、求める電流の式は、次式となる。
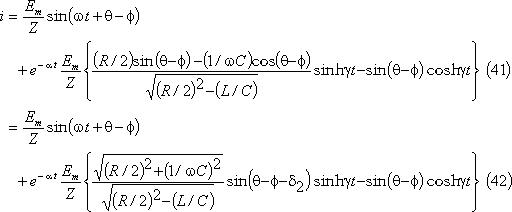
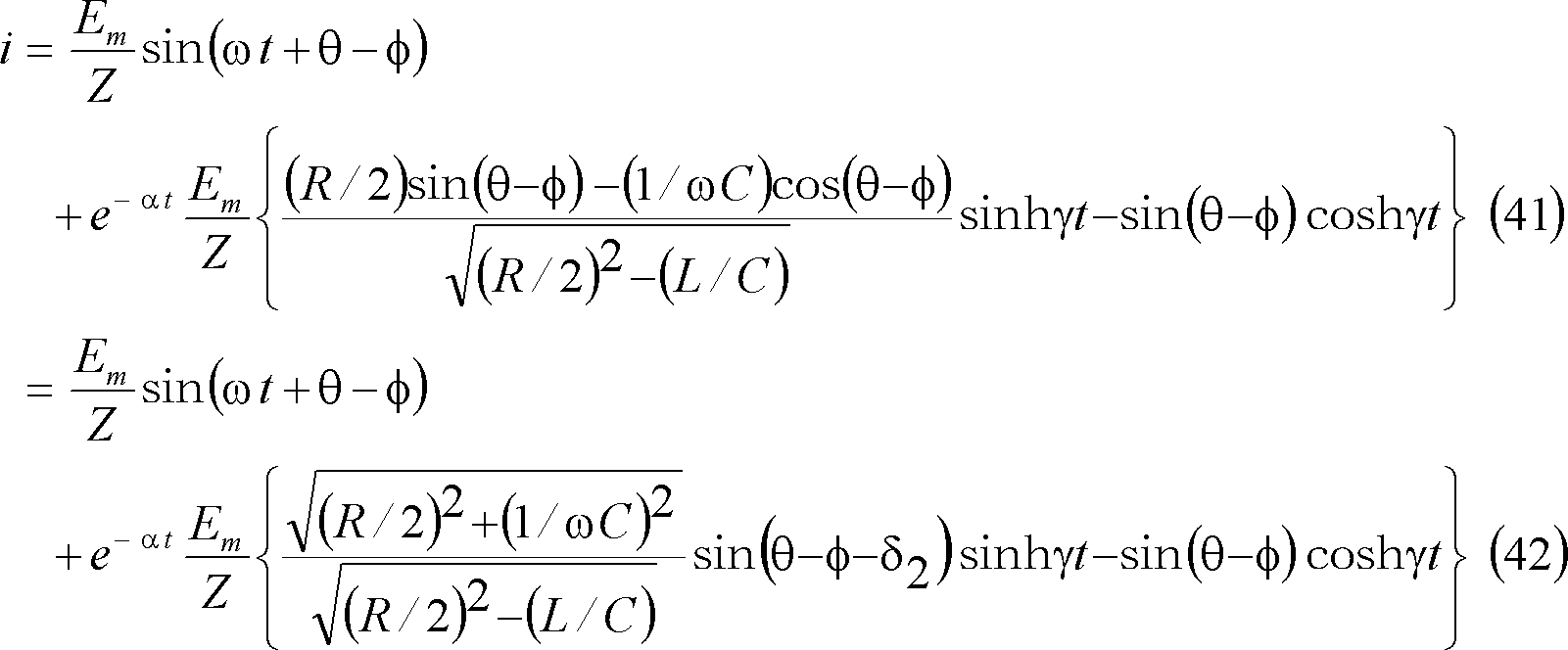
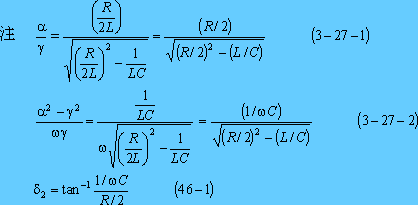
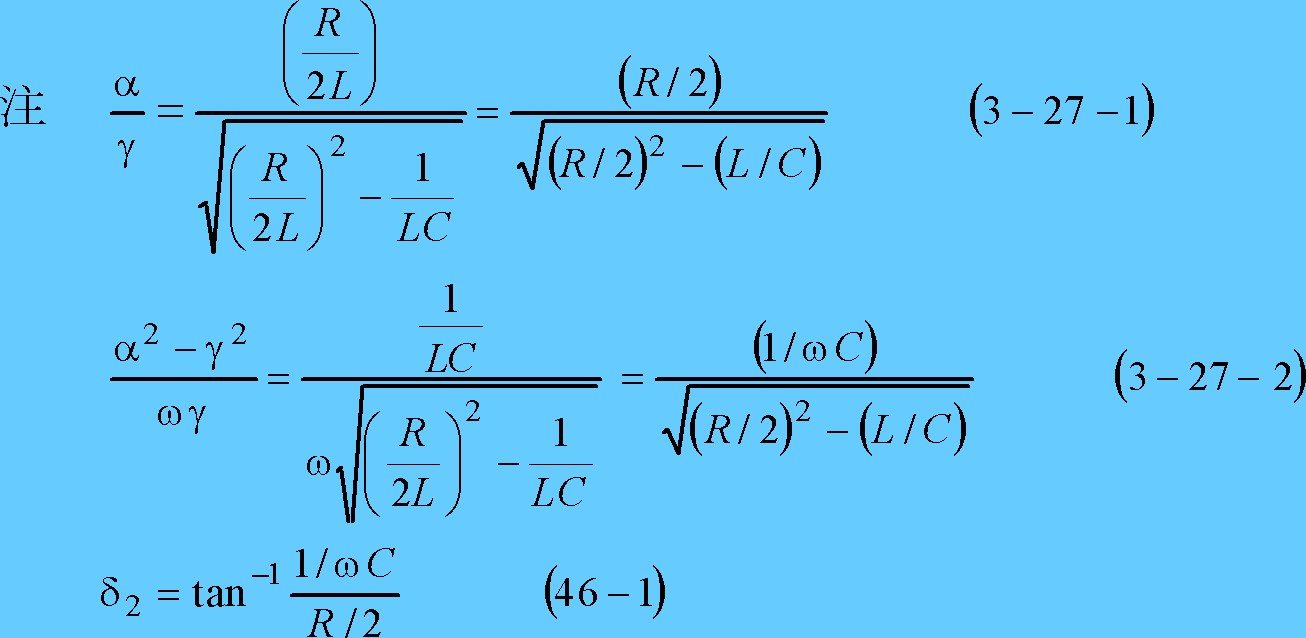
第11図にこの場合の電流波形を示す。
第11図 β<0(非振動形)の場合の電流波形
③
![]()
![]() の場合
の場合
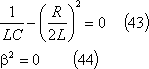
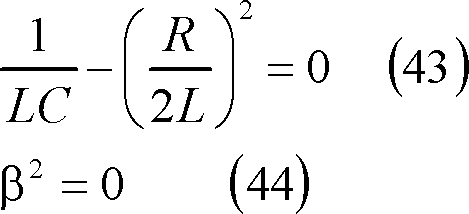
なので、
![]()
![]() は、
は、
となり、巻末の参考計算[3−3]によって、電流が次のように求まる。
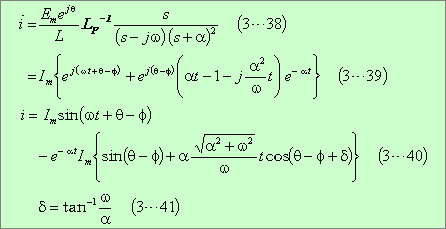
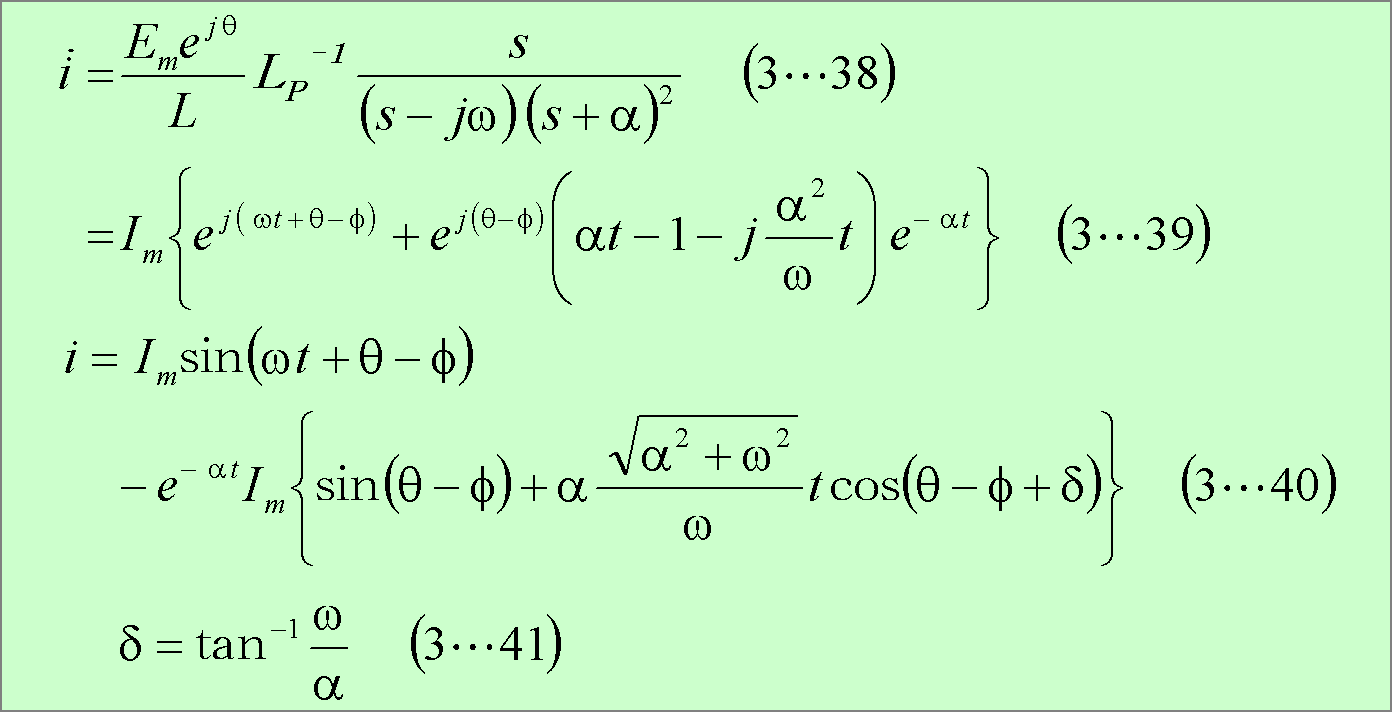
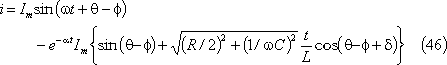
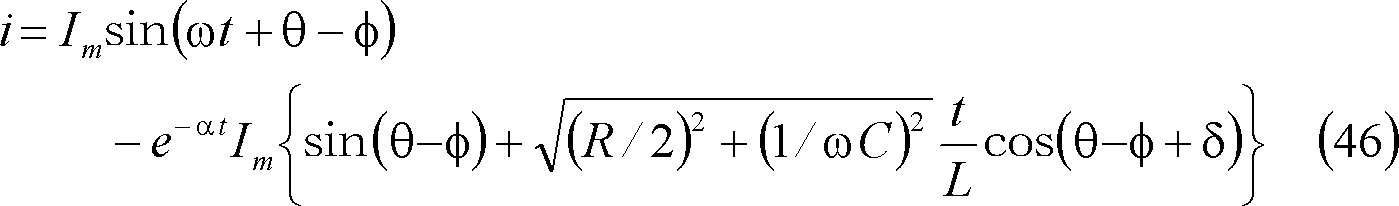
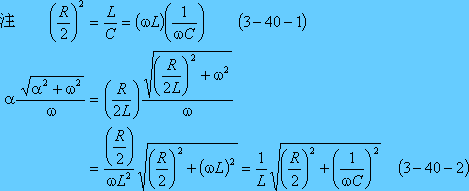
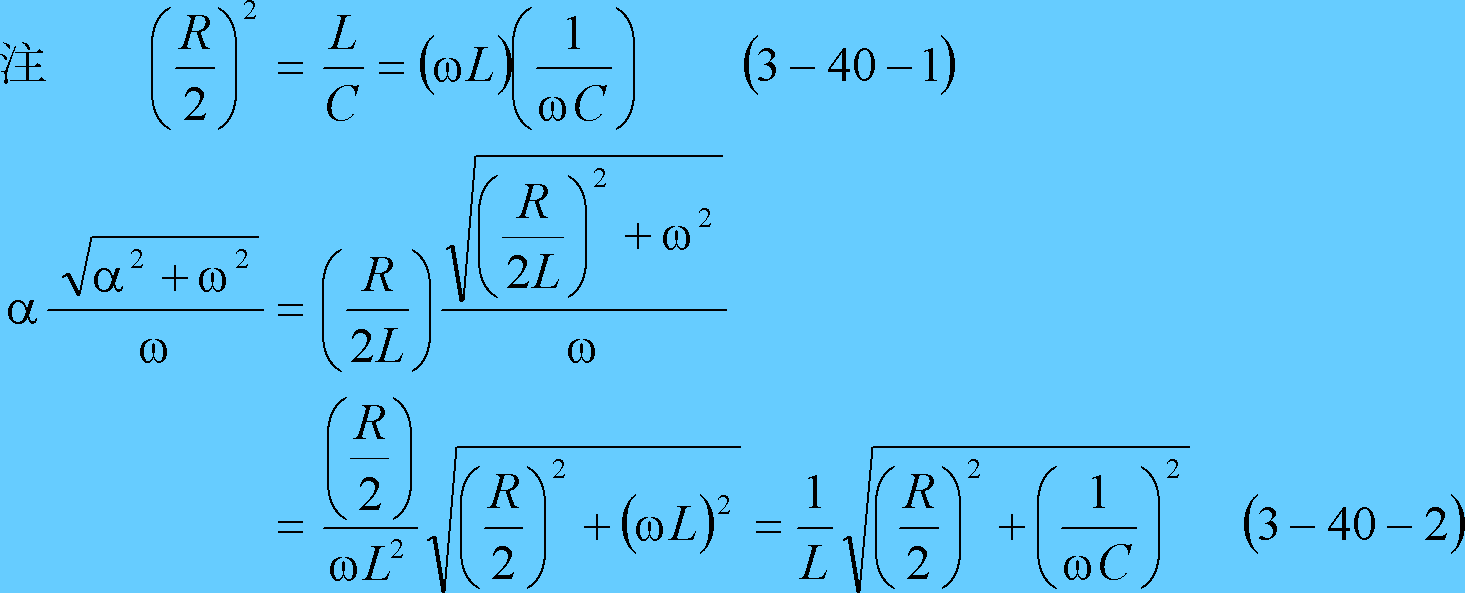
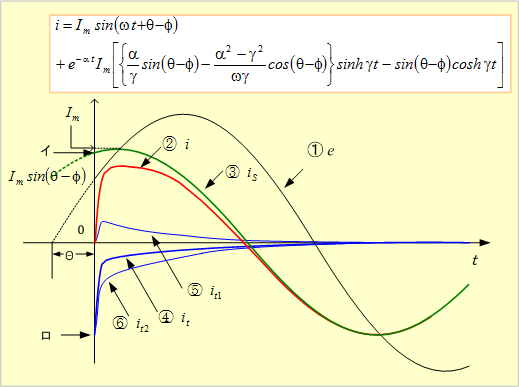
第12図にこの場合の電流波形を示す。
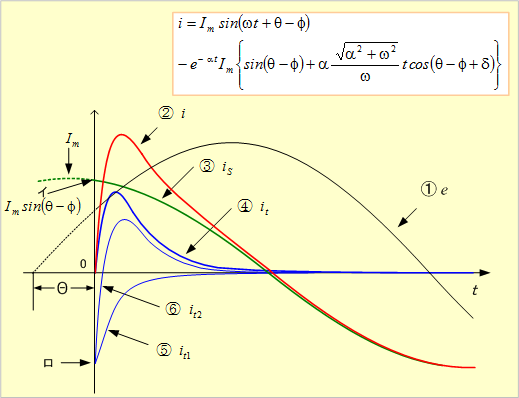
第12図 β=0(臨界形)の場合の電流波形
第1表 s回路計算のルール
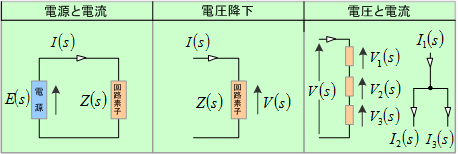
第2表 回路定数のs記号式表示
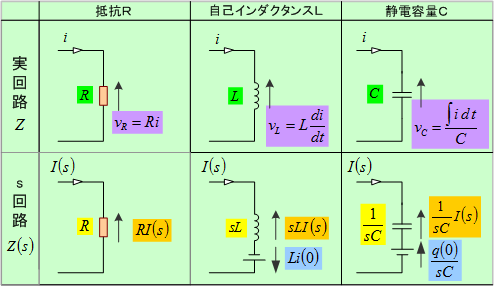
付表 主要関数のラプラス変換と基本法則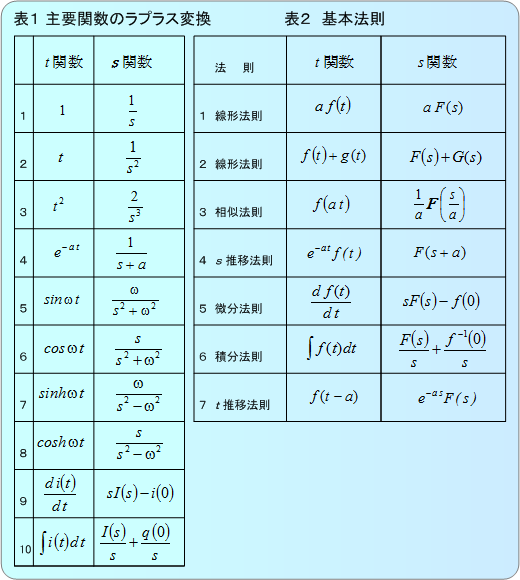
参考計算[1] 例題1関連の逆変換公式とその導き方
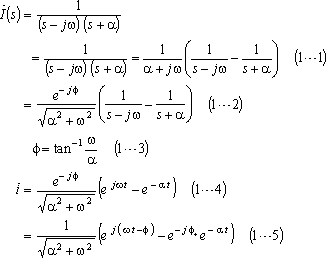
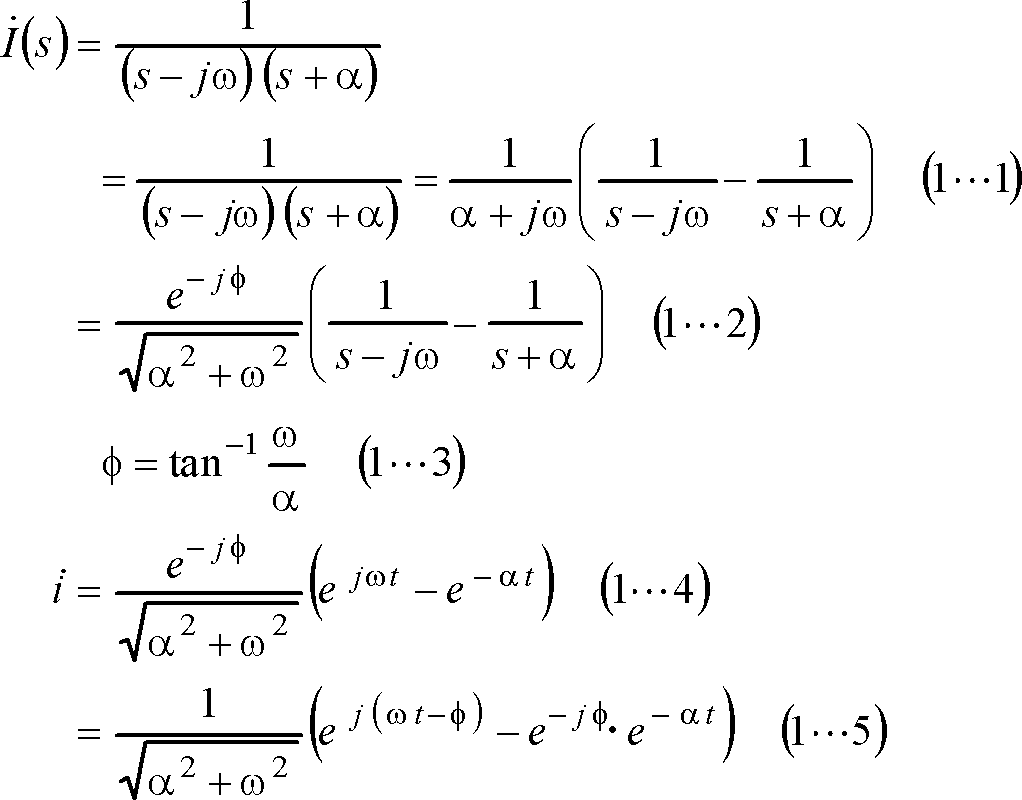
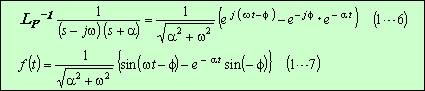
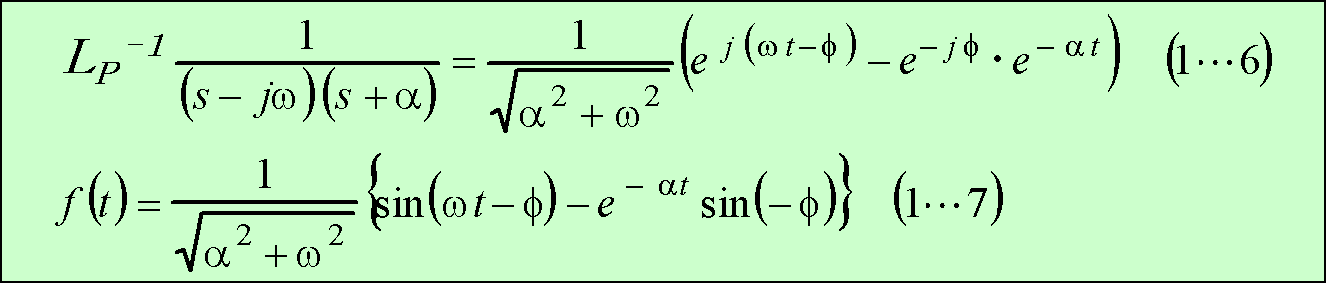
参考計算[3−0] 例題3関連の逆変換公式((3…1)式)とその導き方
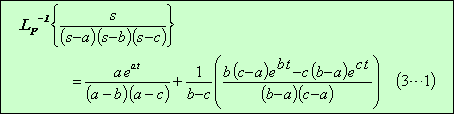
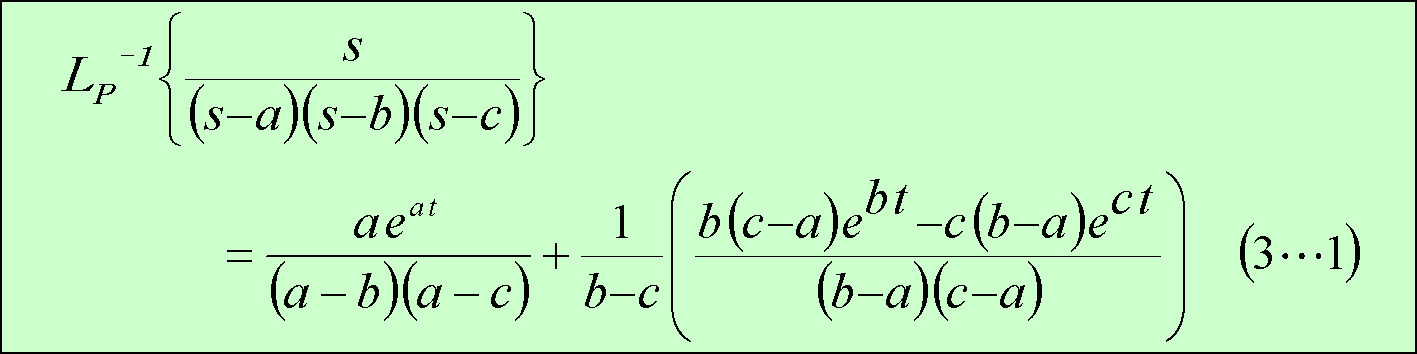
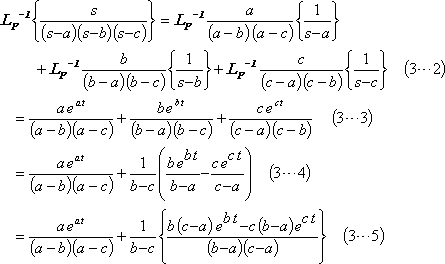
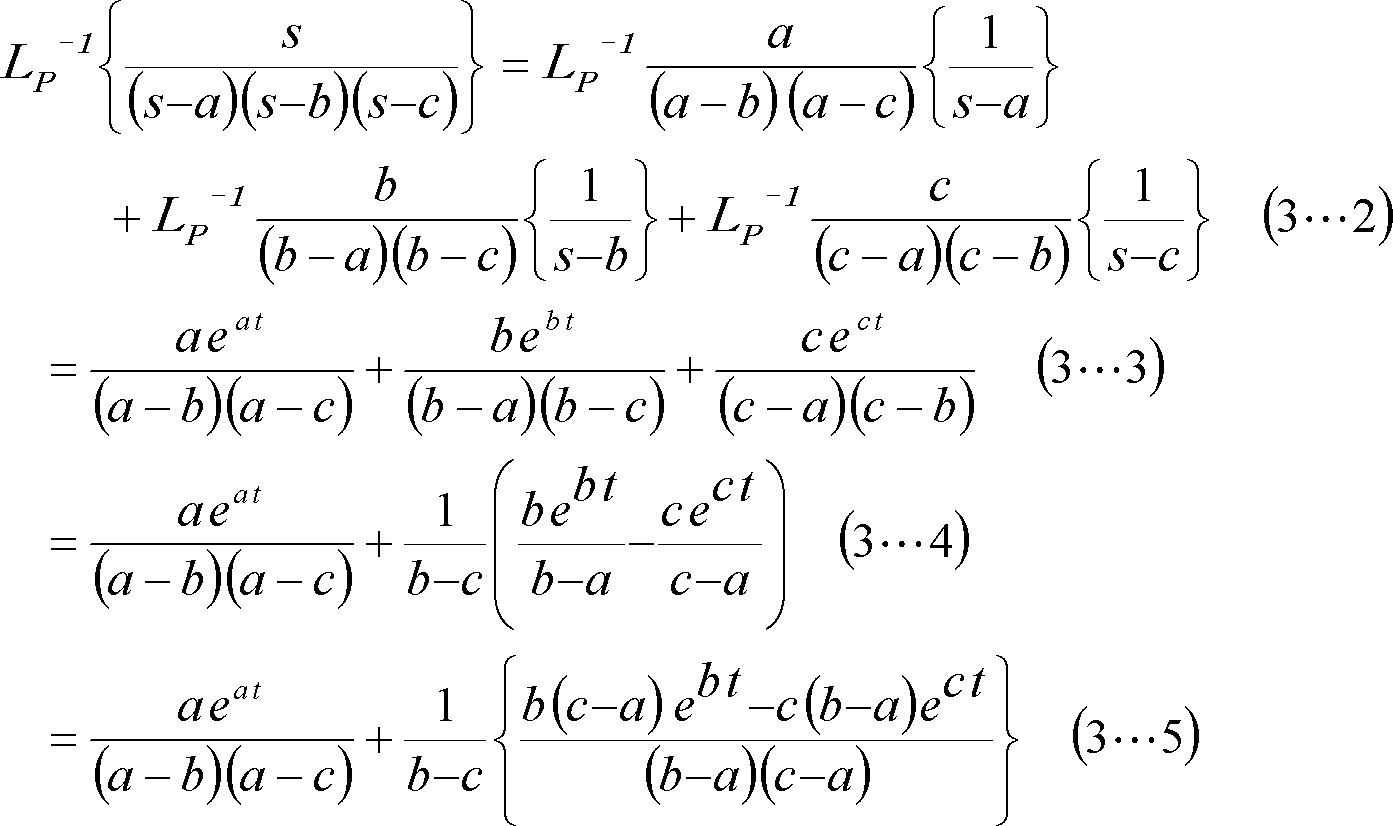
参考計算[3−1] 例題3の参考計算(1) β>0の場合の逆変換式の求め方
の場合は、上記の変換公式(3…1)式 において、
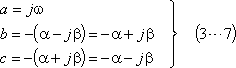
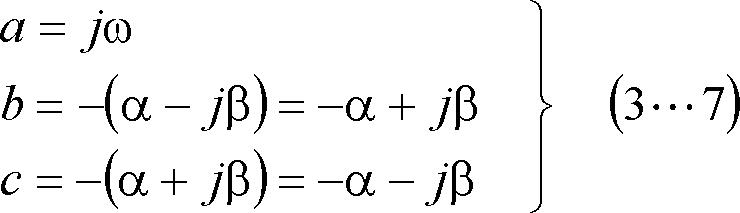
とおき、
である場合は、変換公式(3…1)式の各部は、
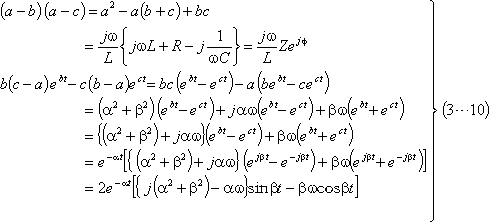
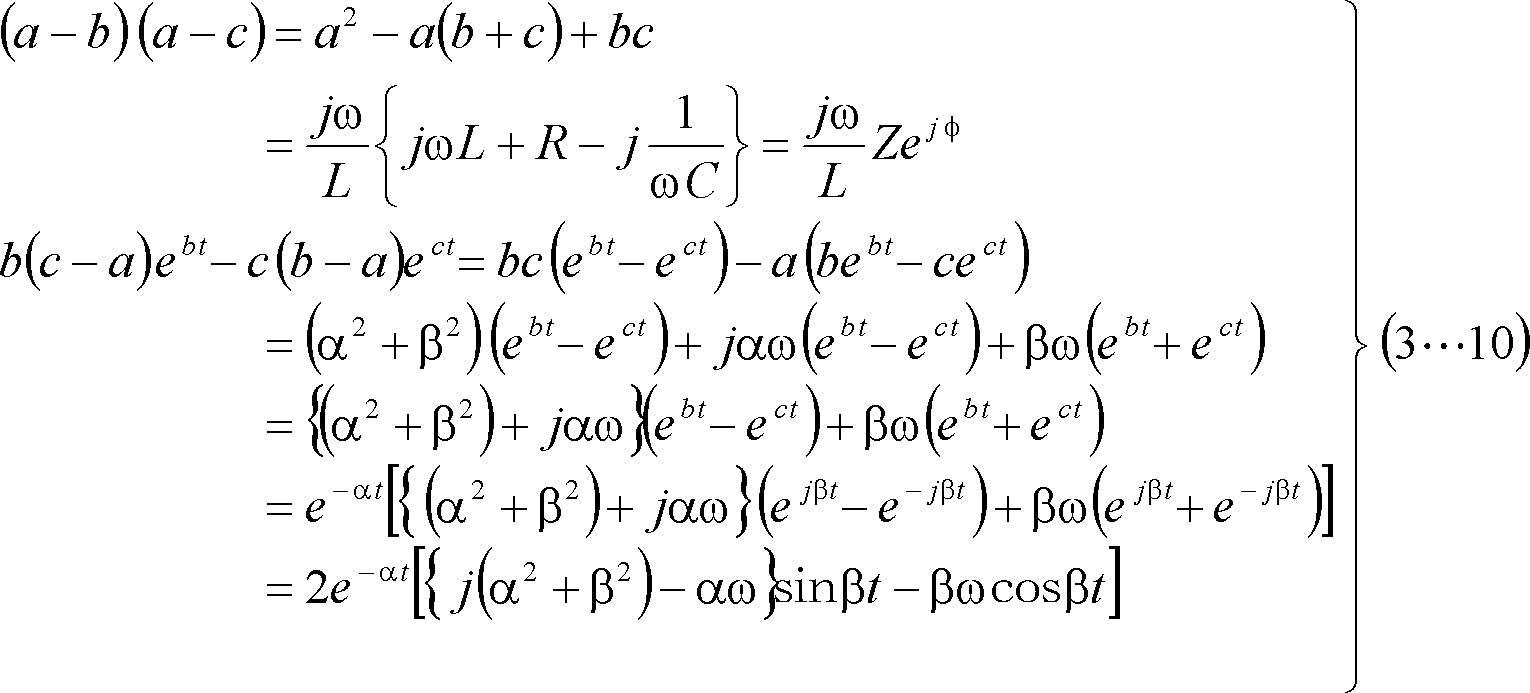
となるので、(3…6)式に逆変換公式(3…1)を適用すると、次のように計算できる。
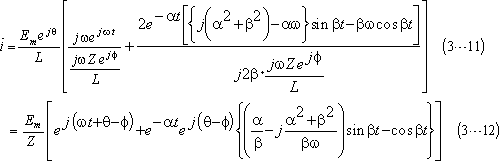
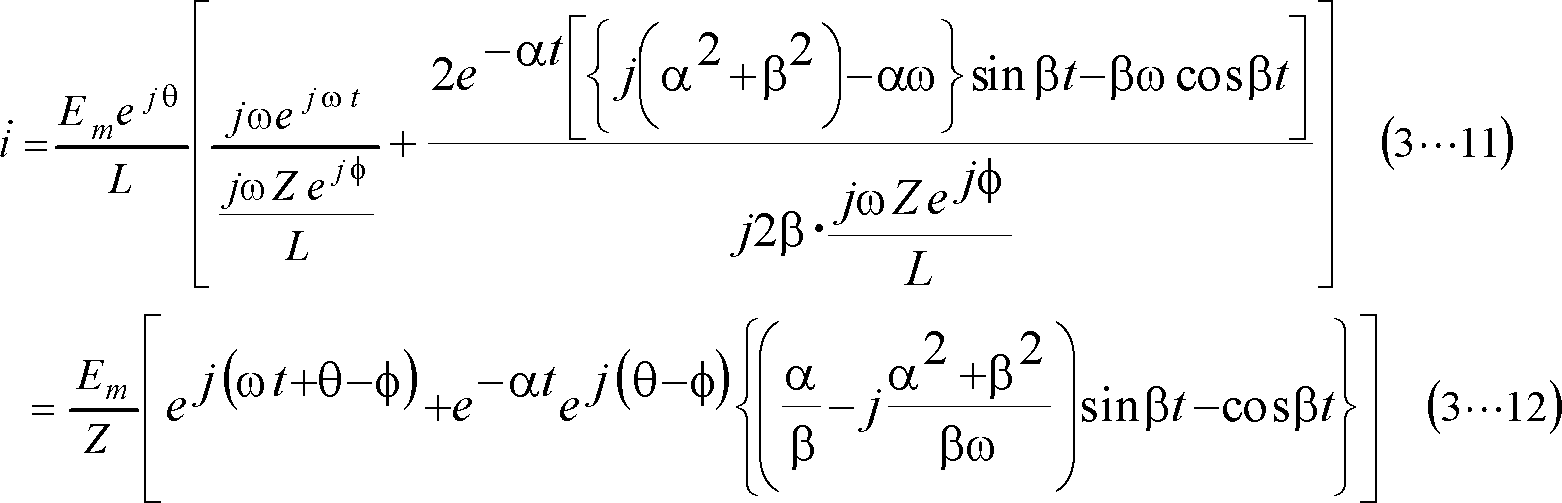
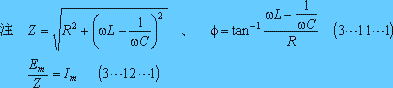
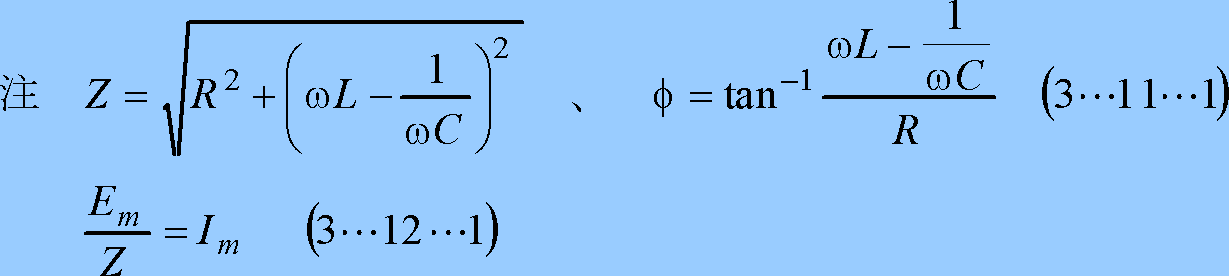
求める電流は、上式の虚数部なので、
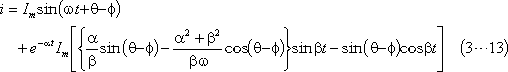
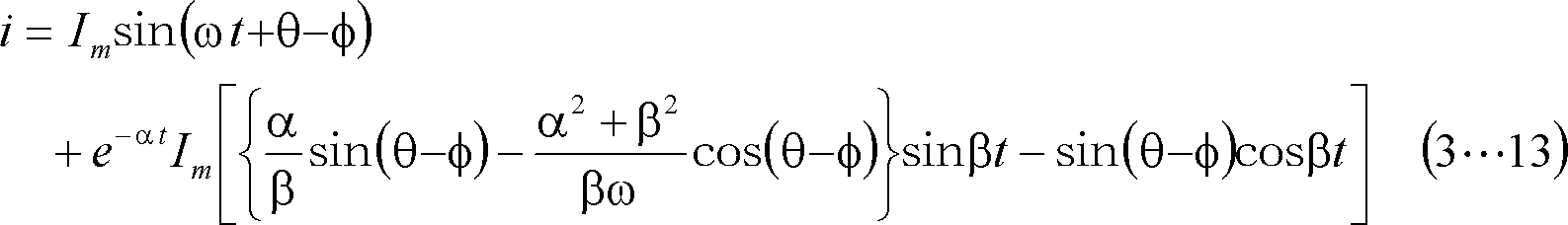
となる。以上をまとめると次のようになる。
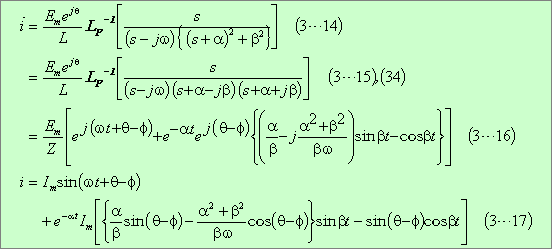
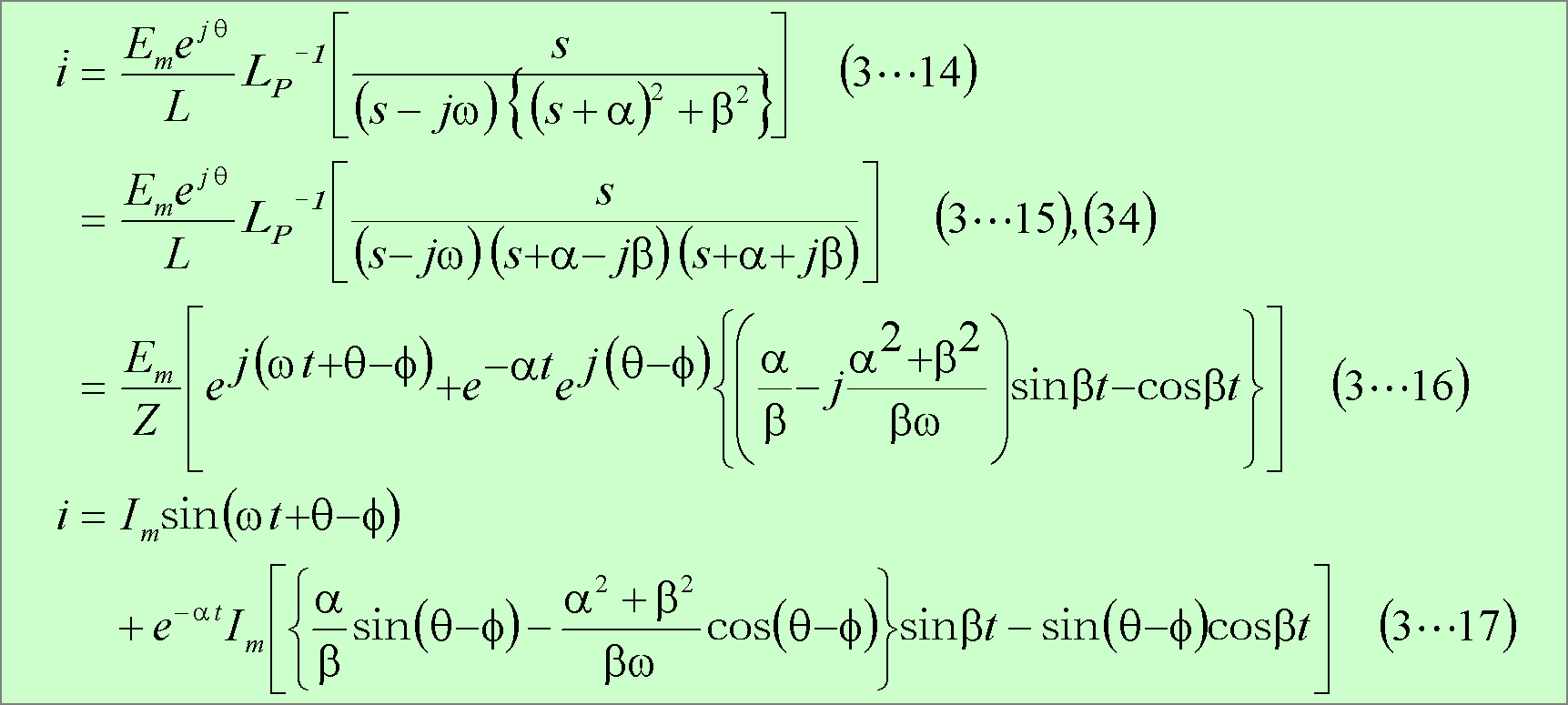
参考計算[3−2] 例題3 β<0の場合の逆変換式の求め方
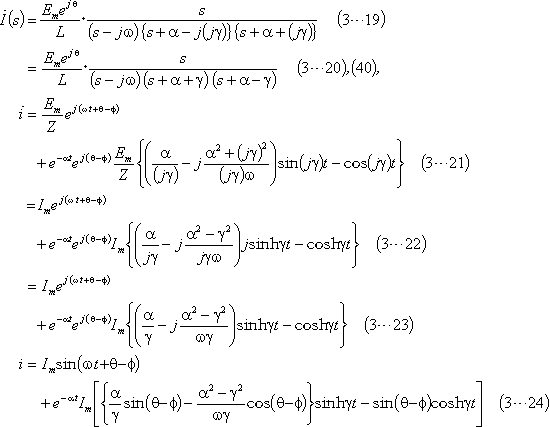
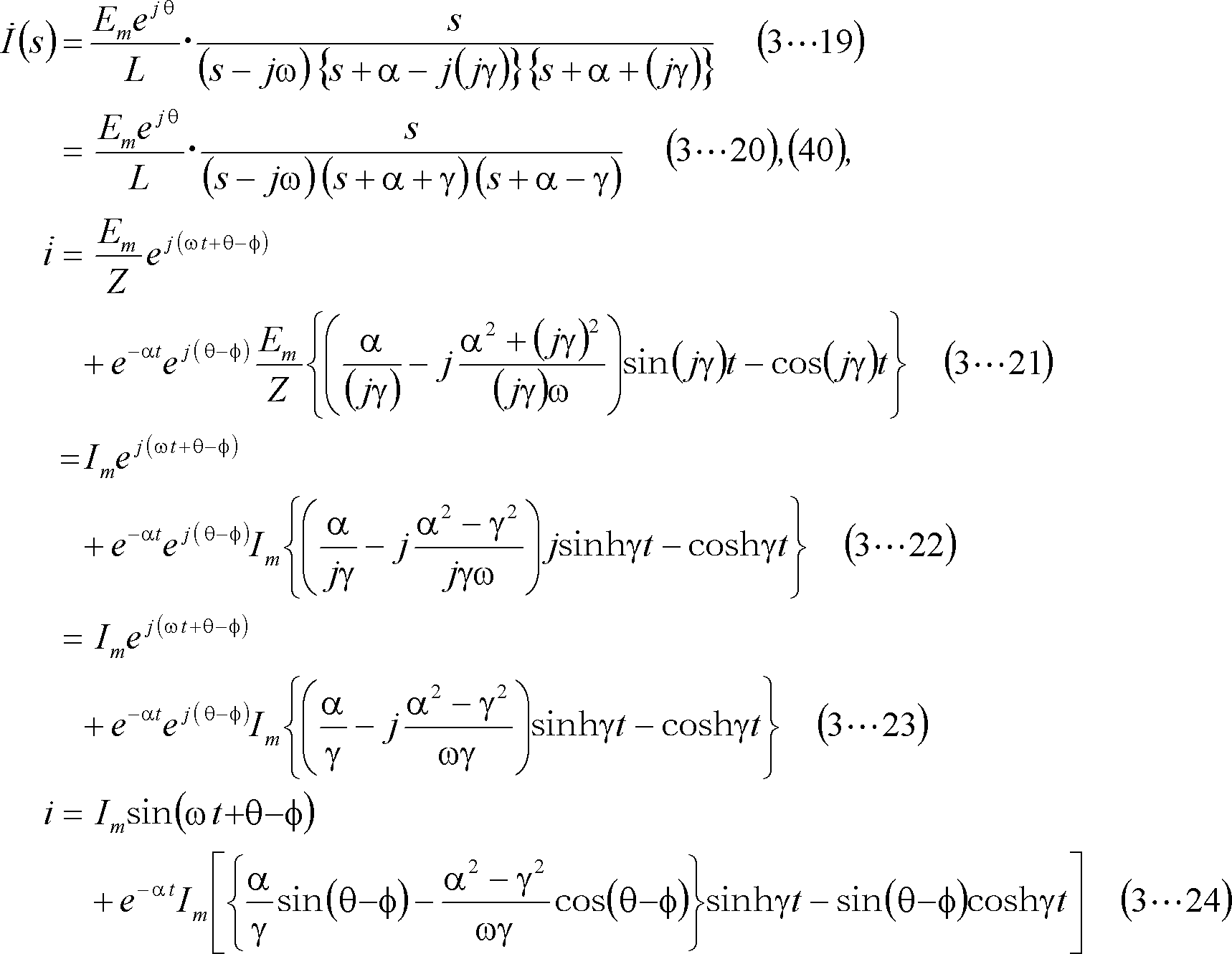
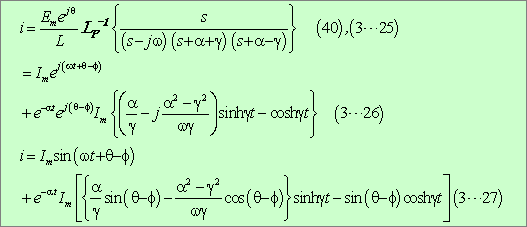
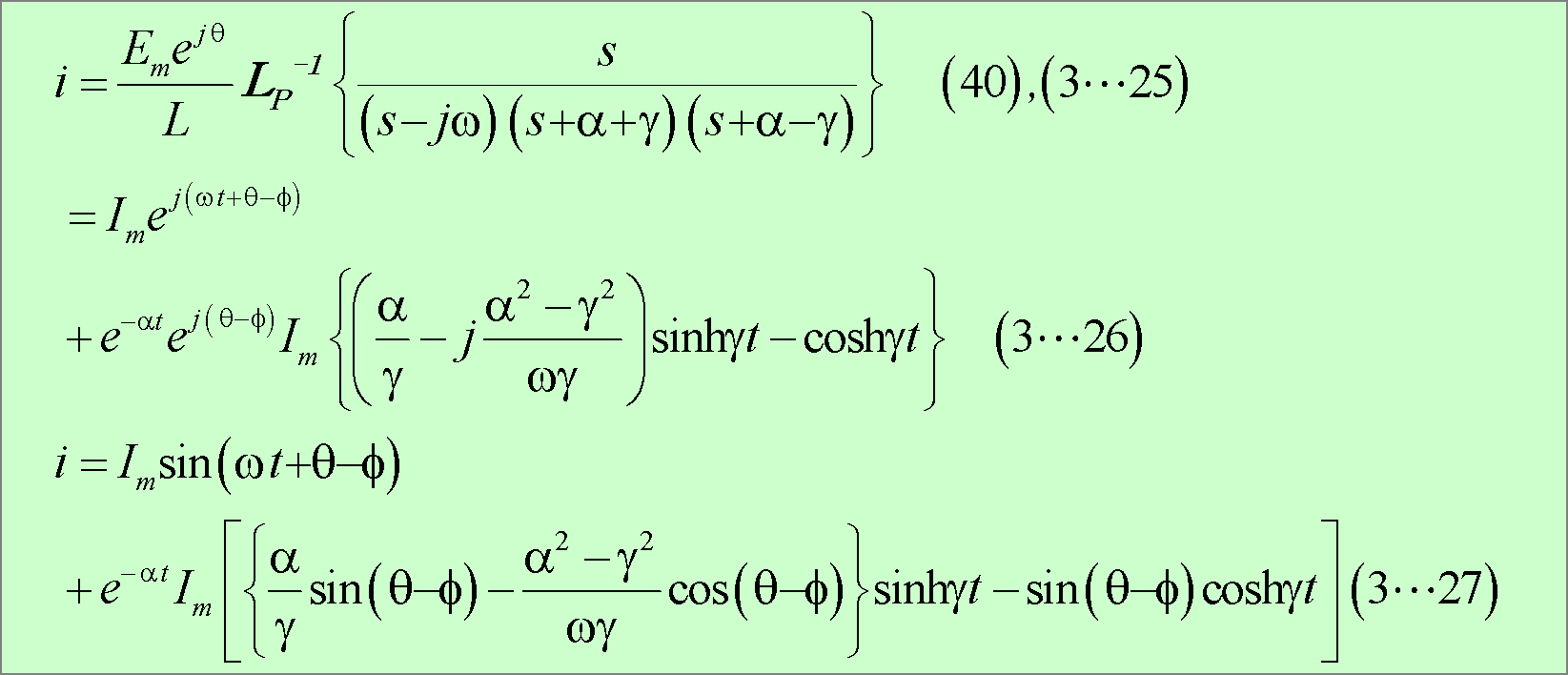
参考計算[3−3] 例題3 β=0の場合の逆変換式の求め方