〜終わり〜
■ぜひアンケートにご協力下さい■


電磁気現象は微分方程式で表され、一般的には微分方程式を解くための数学的に高度の知識が要求される。ラプラス変換は、計算手順さえ覚えれば、代数計算と変換公式の適用により微分方程式が解ける数学知識への負担が少ない解法である。このシリーズでは電気回路の過渡現象や制御工学等の分野での使用を念頭に置いて範囲を限定して、ラプラス変換を用いて解く方法を解説する。今回は、直流RLC直列回路の過渡現象の解き方について解説する。
(1) 回路の電圧方程式を立てる(回路方程式、電圧方程式)。
(2) 電圧方程式をラプラス変換する(ラプラス変換、ts変換、s回路方程式)。
(3) (2)のs回路方程式を求めたい量のs関数について解く。(s回路計算)。
(4) 求めている量のs関数をラプラス逆変換して、その量のt関数を導出する(ラプラス逆変換、st変換)。
第1図のように、起電力Eと、抵抗R、自己インダクタンスL、静電容量Cの直列接続からなる回路において、t=0でスイッチSを閉じた時、回路に流れる電流を求めてみよう。ただし、静電容量CにはS投入前には電荷はなかったものとする。
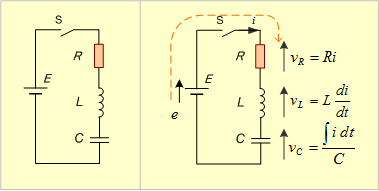

第1図 RLC直列回路 第2図 回路各部の電圧と電流
【解き方】
(1) 回路方程式
起電力、電流、電圧降下の正方向を第2図のように定めると、回路各部の電圧は図中の式で示される。この結果、回路の電圧方程式は次式となる。
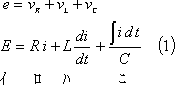
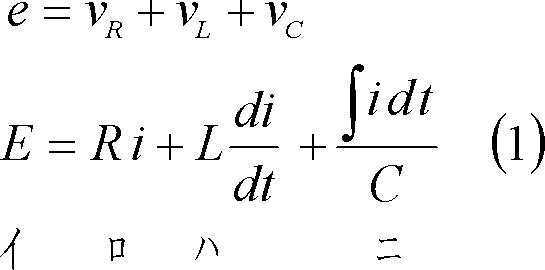
(2) ラプラス変換(s回路方程式)
この電圧方程式をラプラス変換すると(2)式となり、初期値を入れると(3)式、同式を整理して(5)式のs回路方程式が得られる。
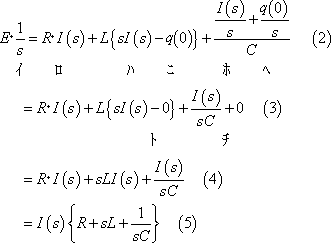
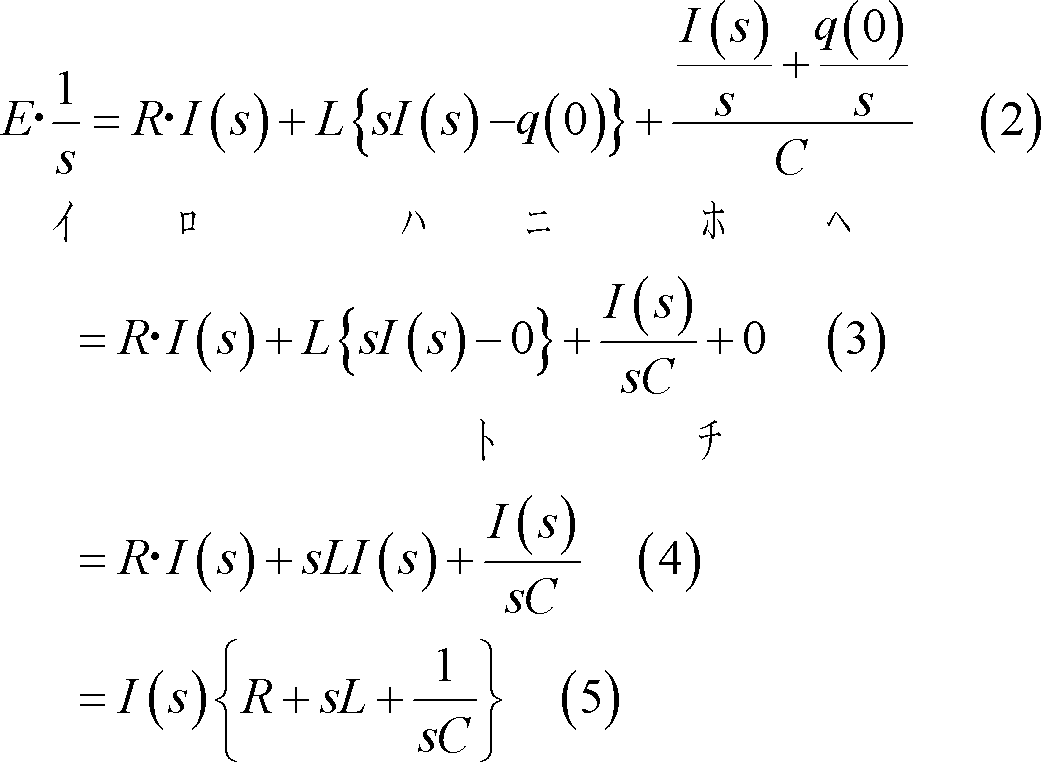
(3) s回路計算
(5)式のs回路方程式を求めたい量のs関数について解く。
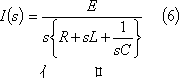
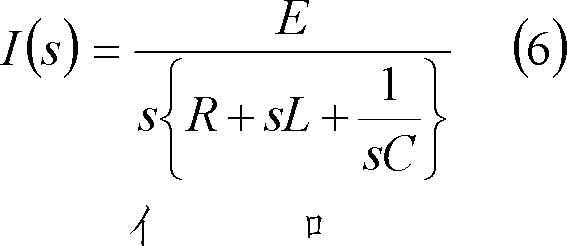
(4) ラプラス逆変換
求めている量のs関数(I(s))をラプラス逆変換して、その量のt関数(i)を導出する。I(s)を次式のように内容的に整理する。
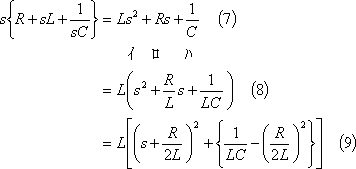
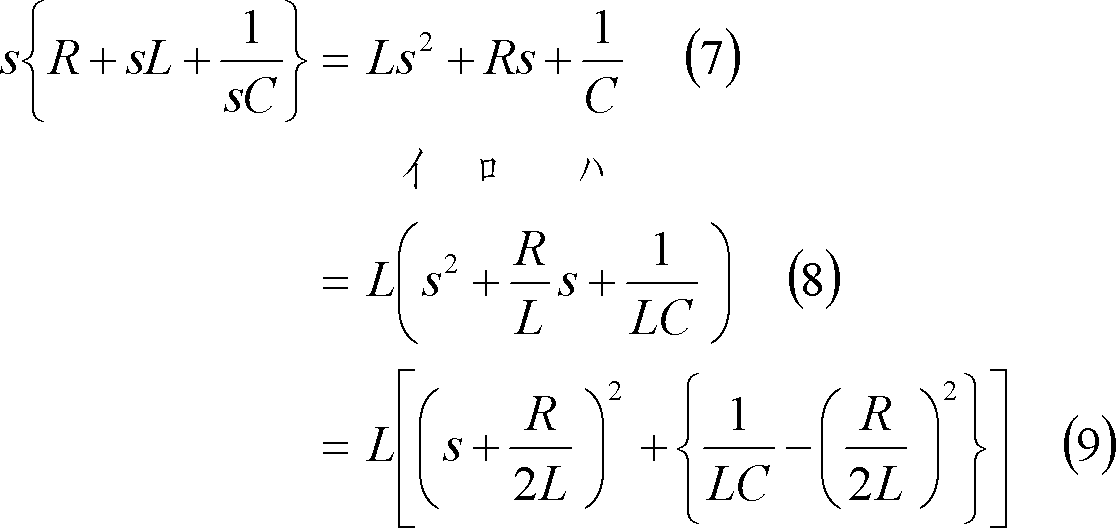
(9)式は{ }内の大小関係によって次の3ケースが考えられる。
ケース1
![]()
![]()
の場合、
ここで、
![]()
![]() とおき、(9)式の{ }内を、
とおき、(9)式の{ }内を、
とおけば、電流のs関数は次のようになる。
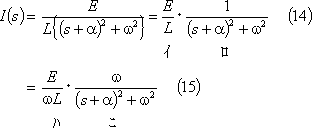
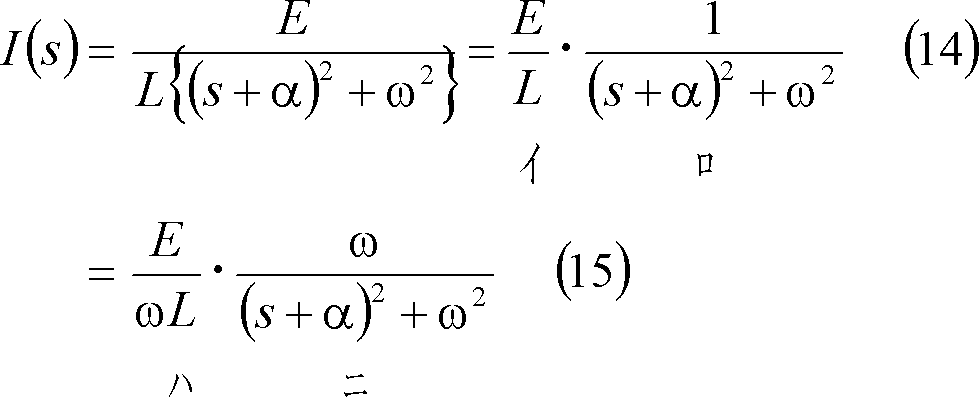
ここで付表2の4番にある「s推移法則」に注目する。
この法則によれば、s関数
![]()
![]() は時間関数に直すと
は時間関数に直すと
![]()
![]() となることを示している。つまり、s関数式のsの部分がすべて「
となることを示している。つまり、s関数式のsの部分がすべて「
![]()
![]() 」となっているs関数式のラプラス変換は、
」となっているs関数式のラプラス変換は、
![]()
![]() である
である
![]()
![]() の
の
![]()
![]() 倍に等しい時間関数であることを意味している。
倍に等しい時間関数であることを意味している。
したがって、(15)式をs推移法則及び付表1の5を参考にしてラプラス逆変換すると、次のように電流が求められる。
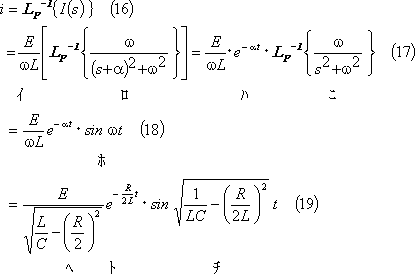
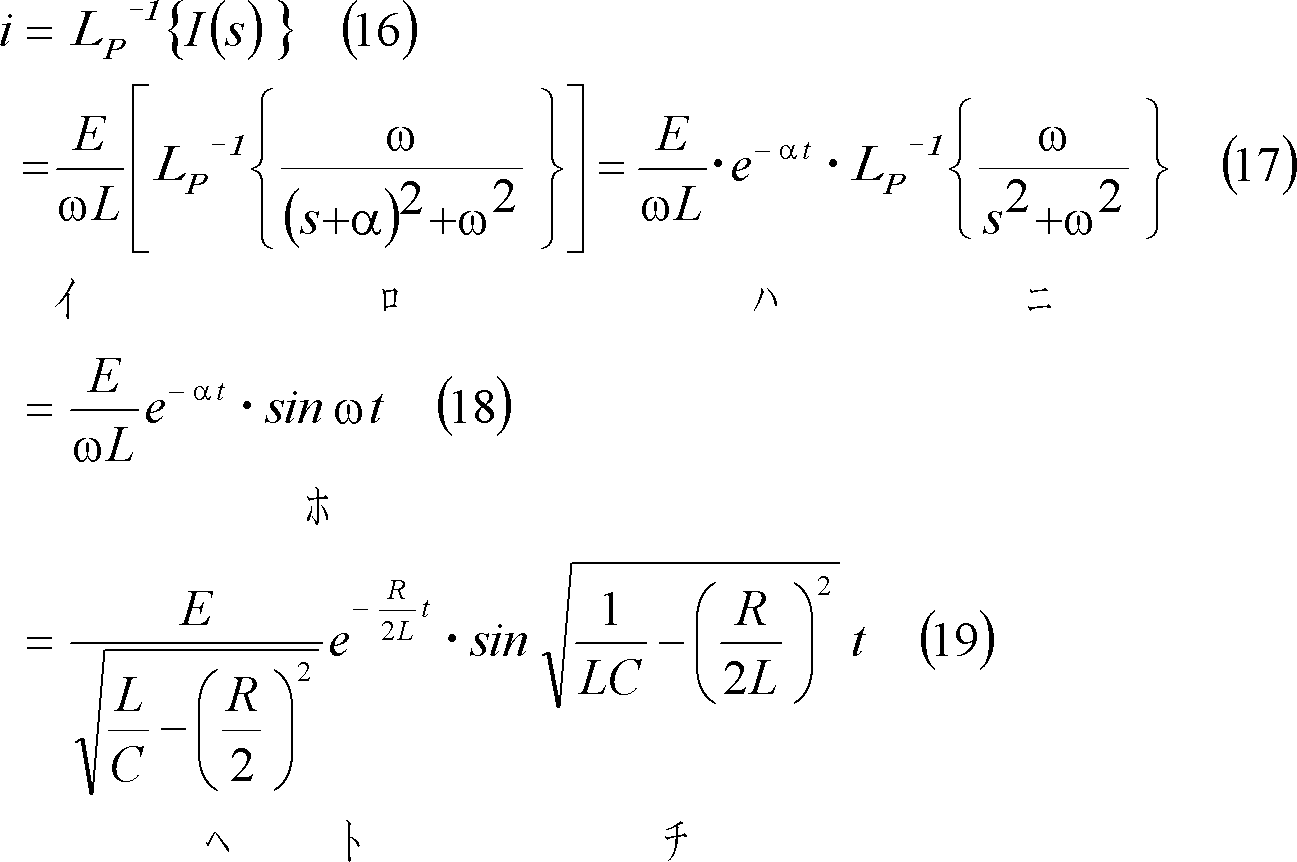
(5) 電流波形は第3図となる。
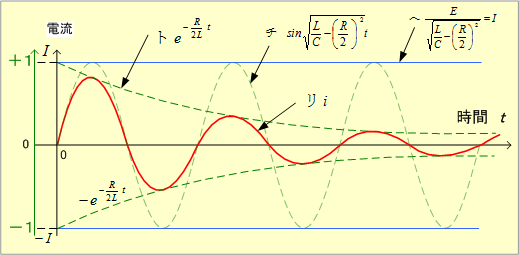

第3図 RLC直列回路の電流波形(ケース1)
ケース2
![]()
![]()
の場合
であり、
とおけば、
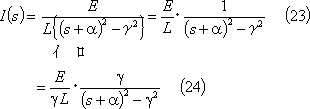
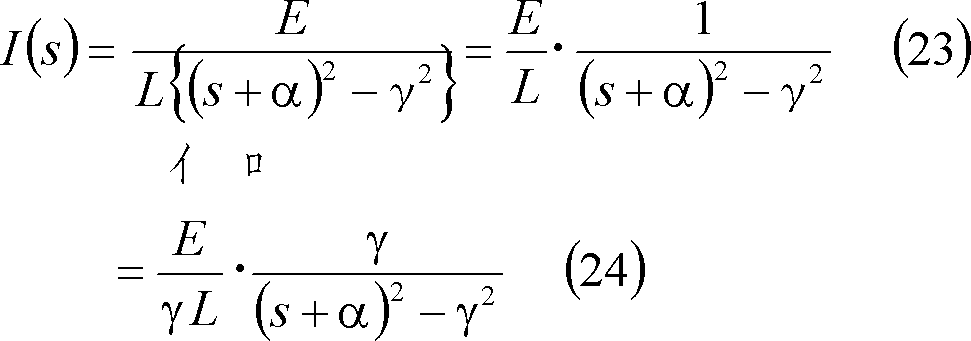
上式を付表1の7にある双曲線関数及び付表2の4にあるs推移法則を使用してラプラス逆変換すると、電流iが求められる。
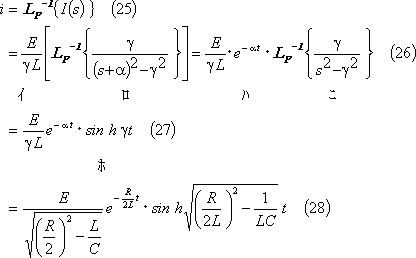
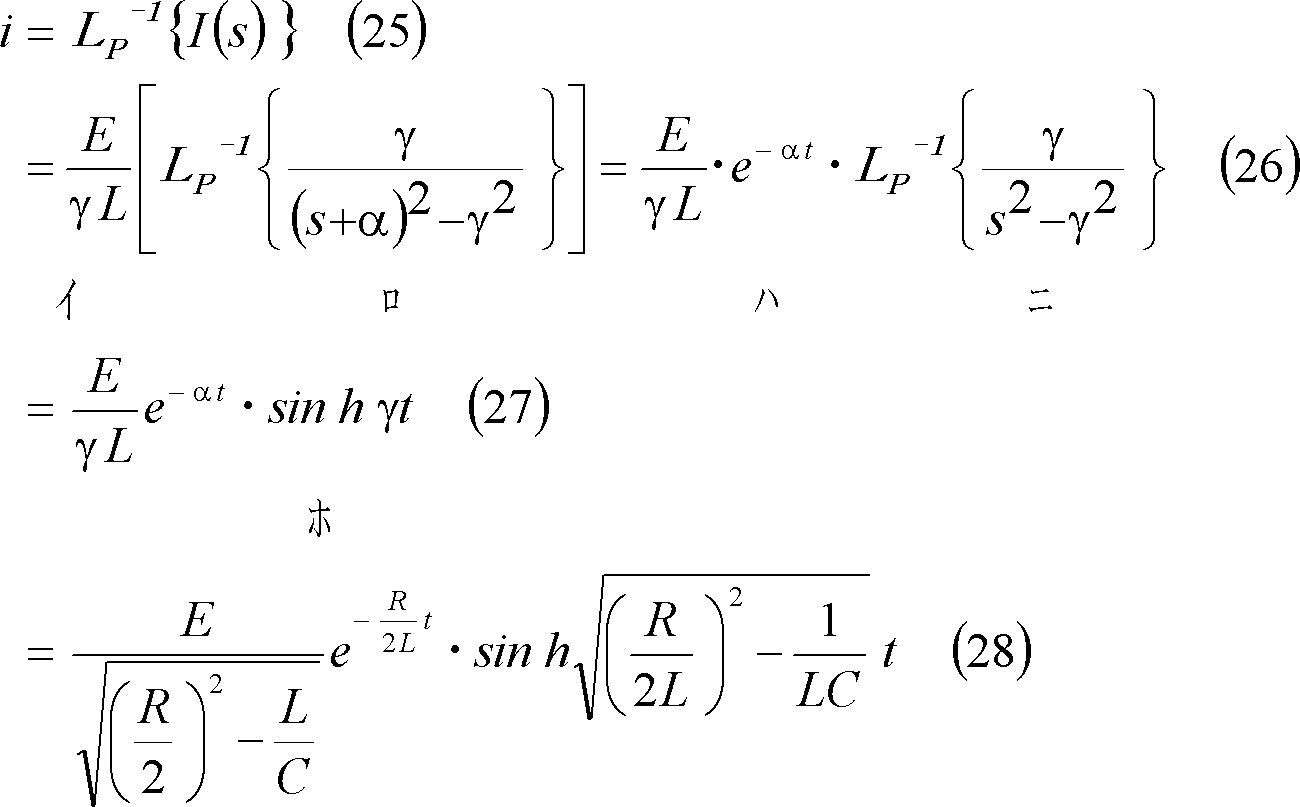
(5) この場合の電流を第4図に示す。
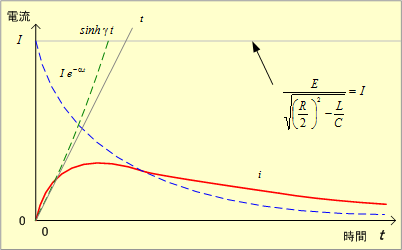

第4図 RLC直列回路の電流波形(ケース2)
ケース3
![]()
![]()
の場合は、
であり、
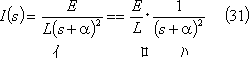
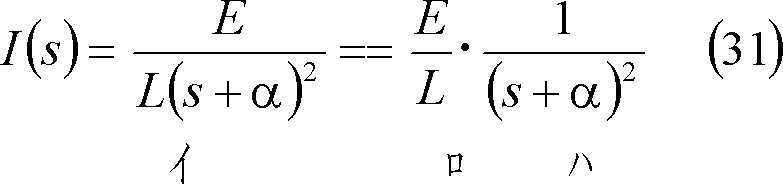
と整形できるので、上式を付表1の3にあるべき関数および付表2の4にあるs推移法則を使用してラプラス逆変換すると、
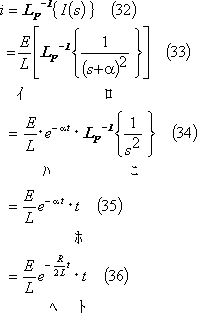
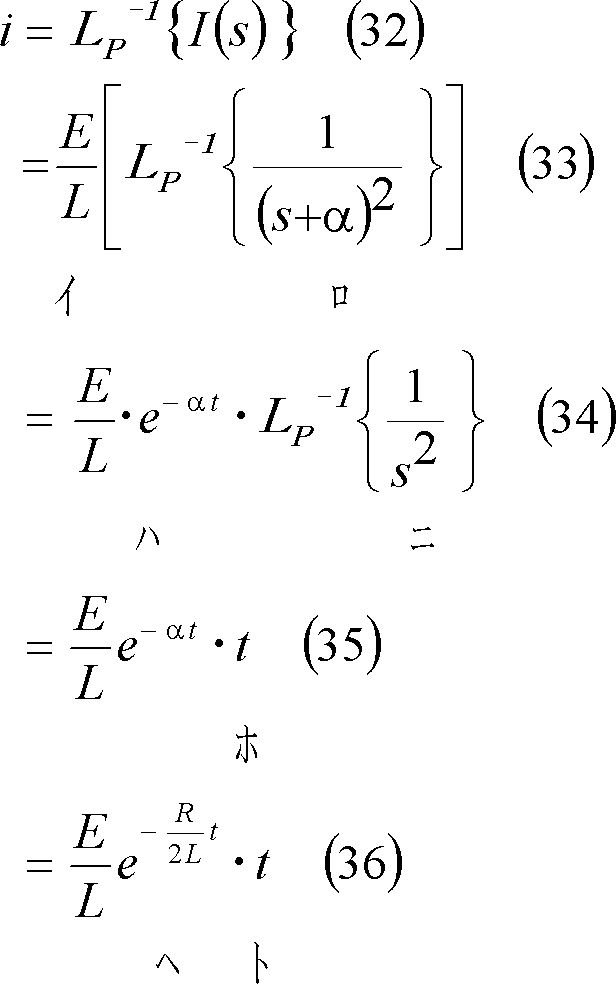
(6) このケースの電流を第5図に示す。
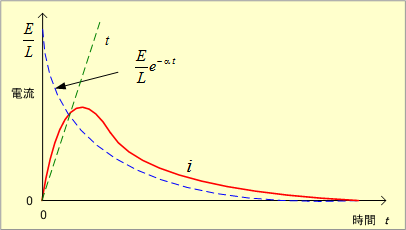

第5図 RLC直列回路の電流波形(ケース3)
三つのケースの電流を比較してみると、第6図となる。
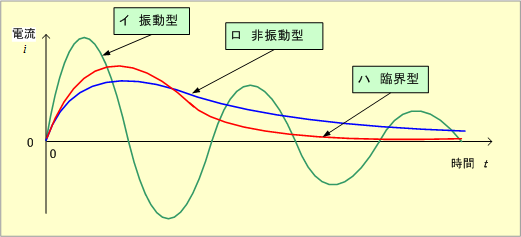

第6図 RLC直列回路の3ケースの電流波形を比較する
問題1 ここで扱った直流RLC直列回路の各ケースについて、t=0でスイッチSを投入してから、電流が最大になるまでの時間T とそのときの電流iTを求めよ。
(答は巻末)
第7図のような2個の抵抗と1個の自己インダクタンスLからなる直並列回路に、t=0のときスイッチSを閉じて直流電圧Eを印加したとき、回路の各枝路に流れる電流を求めてみよう。
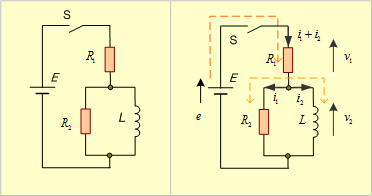

第7図 2RL直並列回路 第8図 回路各部の電圧と電流
(1) 第8図のように、起電力、電流、電圧降下の方向を決め、電圧方程式を立てる。
閉路ESR1R2Eにおける電圧方程式は、
R2とLの並列接続からなる閉路の電圧方程式は反時計方向に計算すると、
(2) 電圧方程式をラプラス変換してs回路方程式をつくる。
(3) s回路方程式を求めている量のs関数について解く。
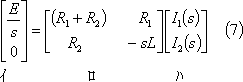
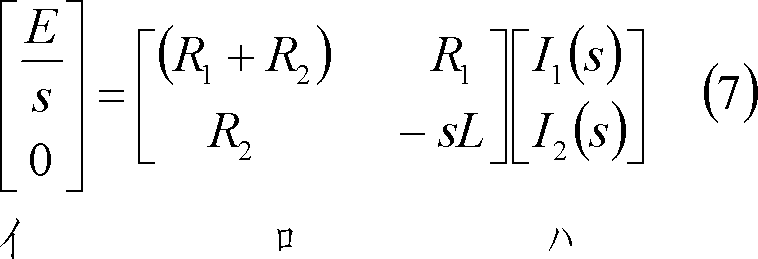
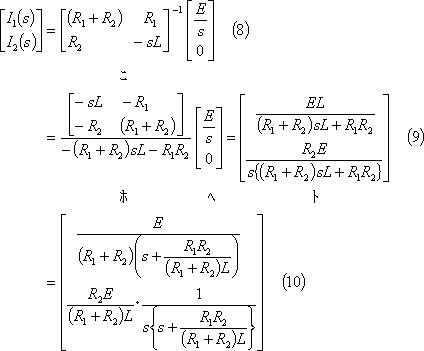
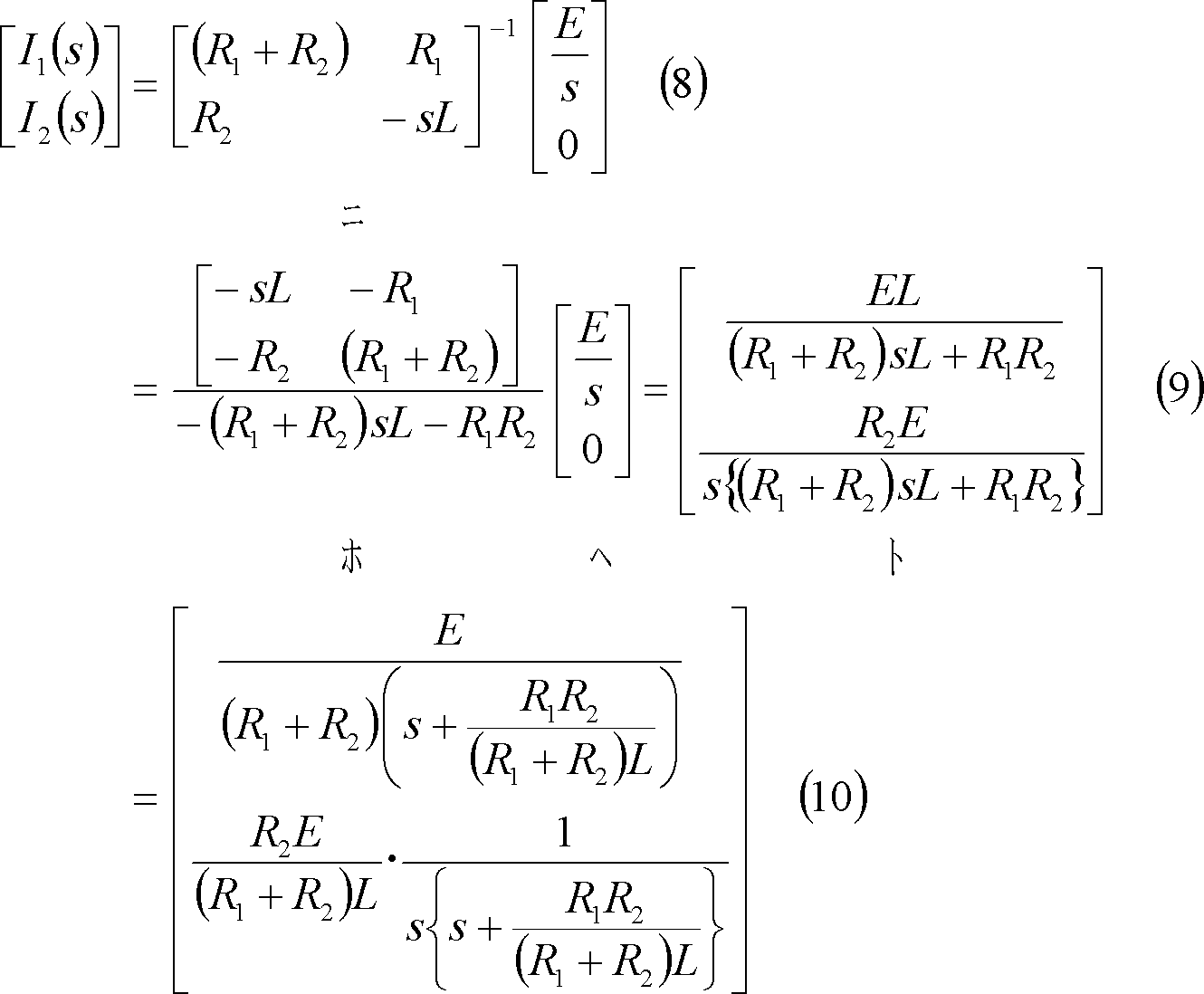
(4) 求めている量のs関数をラプラス逆変換して、求めている量の時間関数(答)を得る。
I1(s)は付表1の4に示す関係を使用して次のように時間関数に変換される。
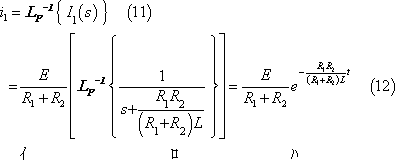
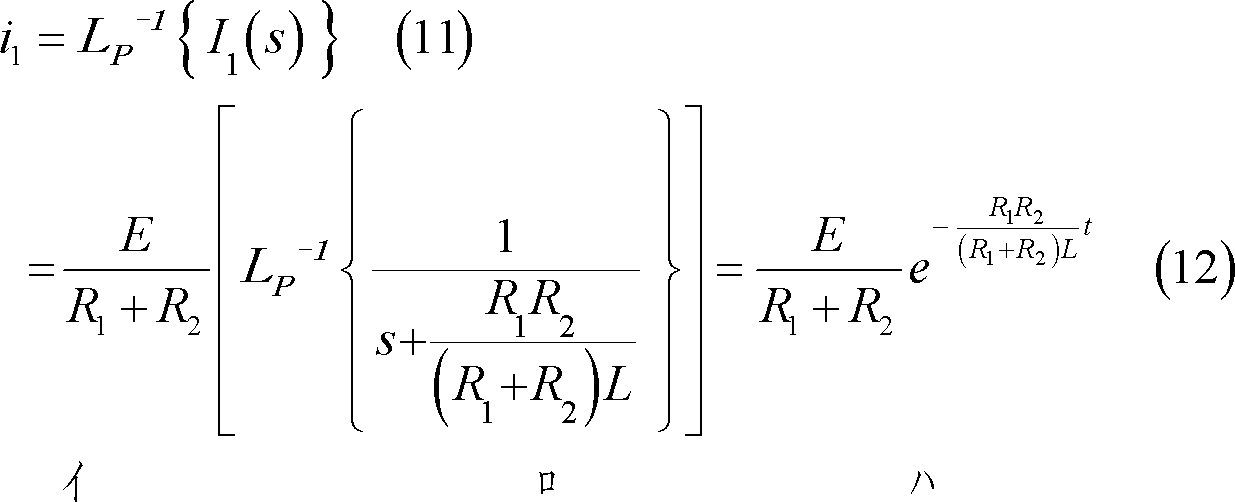
I2(s)は付表1の1および4に示す関係を使用して次のように時間関数に変換される。
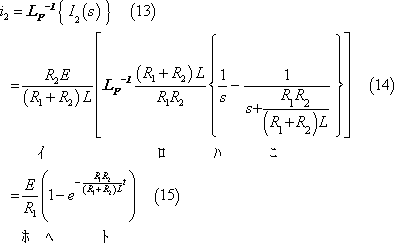
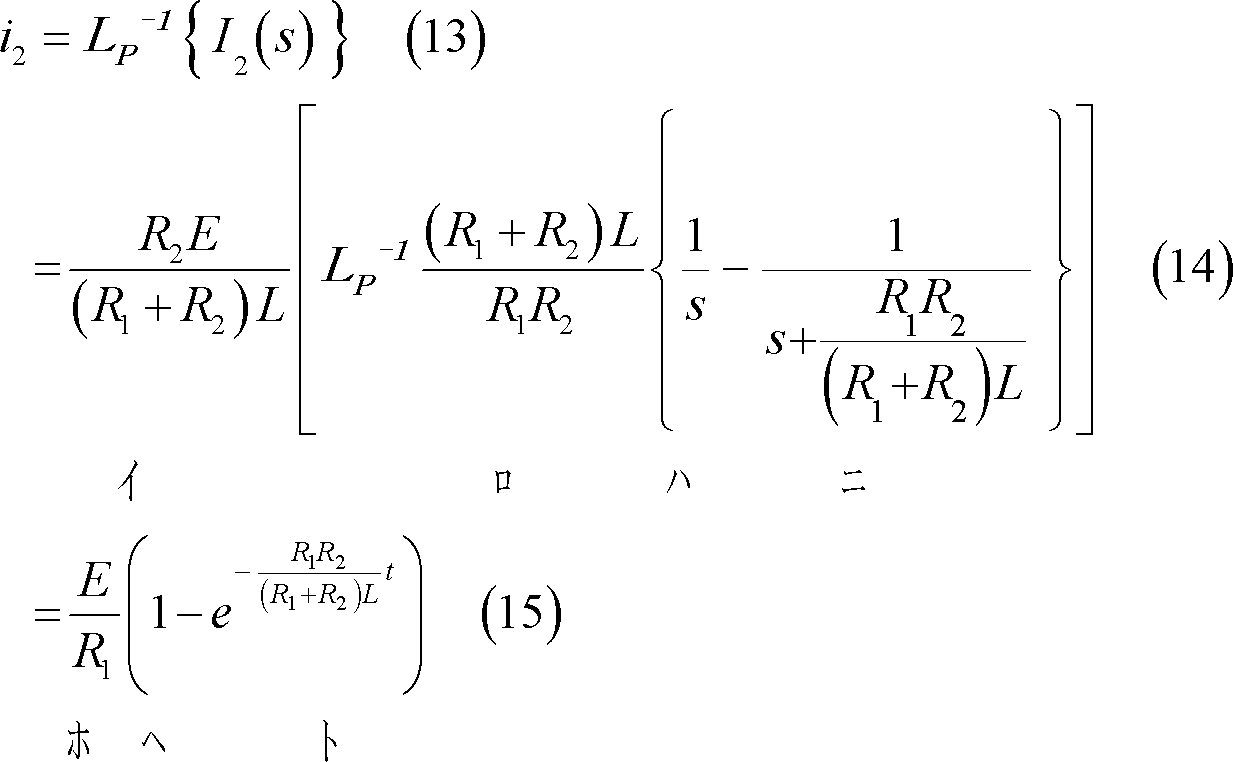
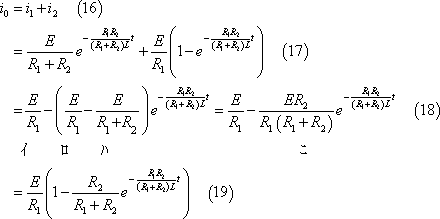
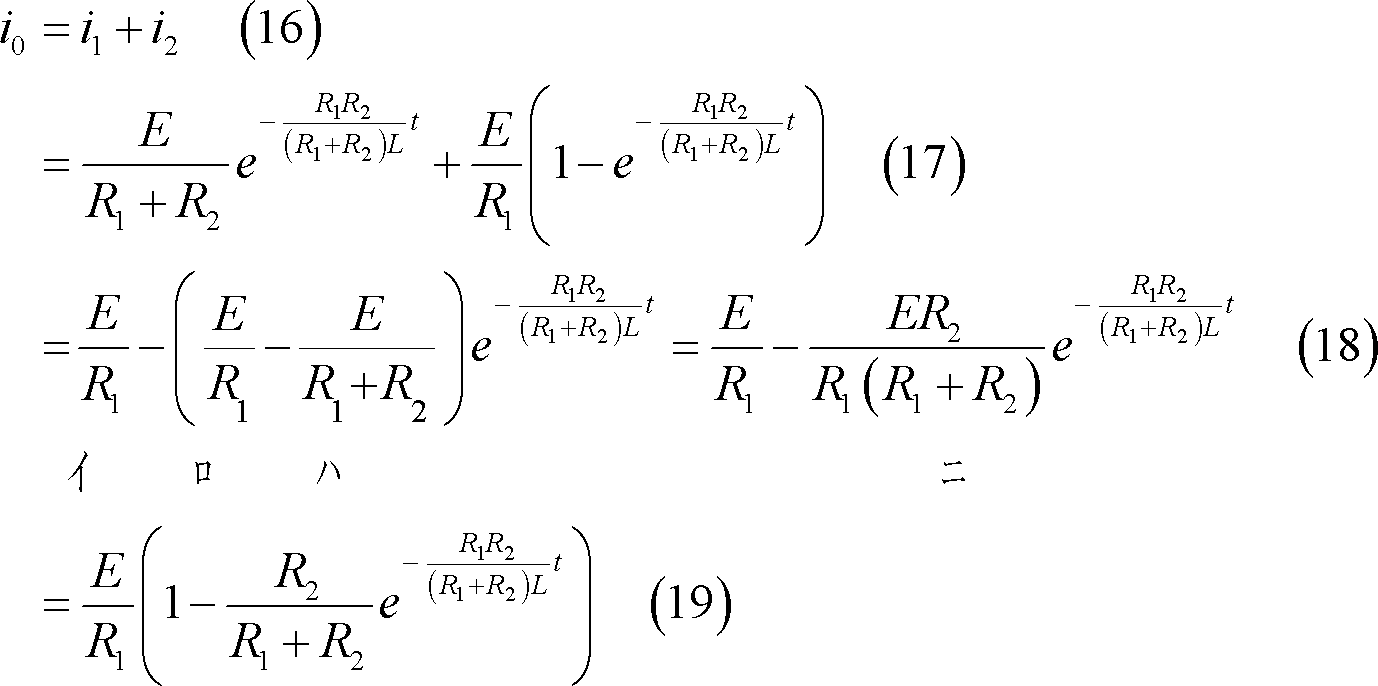
(5) 各枝路の電流
![]()
![]() を第9図に示す。
を第9図に示す。
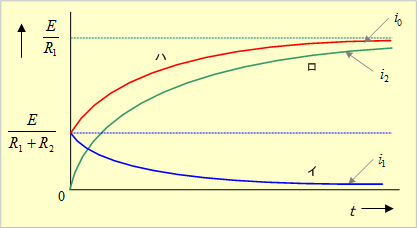

第9図 2RL直並列回路を流れる電流
問題2 2RL直並列回路において、Sを投入してから、i1とi2とが等しくなるまでの時間T を求めよ。
(答は巻末)
(1)ラプラス変換計算法の計算手順を理解し、若干複雑な問題にも応用できるようにする。
[計算手順] ① 電圧方程式 ② ラプラス変換 ③ s回路計算 ④ ラプラス逆変換 の4ステップ。
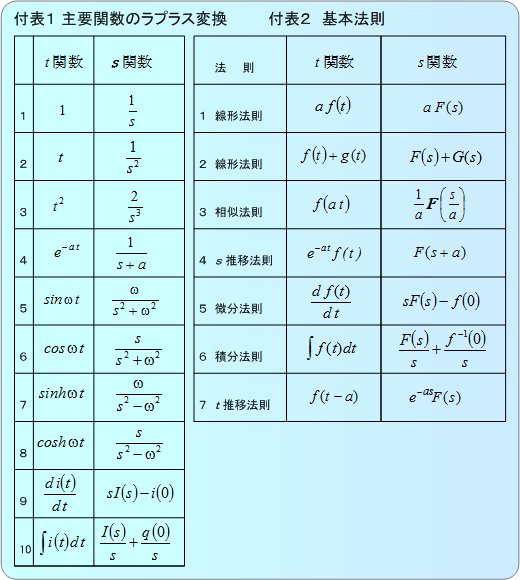
(2)電気工学で使用頻度の高い時間関数(主要関数)について若干複雑なものについても「t関数からs関数に変換する」あるいは「s関数からt関数に変換する」計算ができるように慣れる(付表1)。
(3)ラプラス変換に関する諸法則(基本法則)(付表2)の応用について慣れる。
(4)逆変換の主テクニックである「部分分数分解」が若干複雑な関数形についてもできるようにする。

[問題1の答]
ケース1
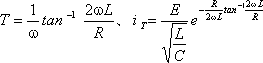
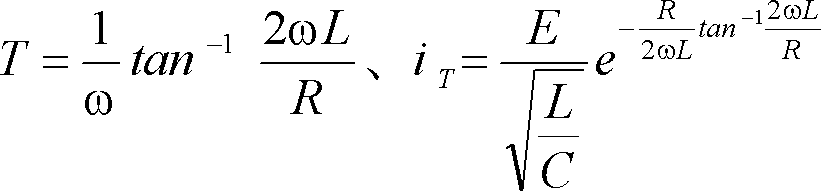
ケース2
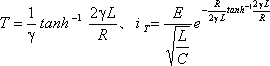
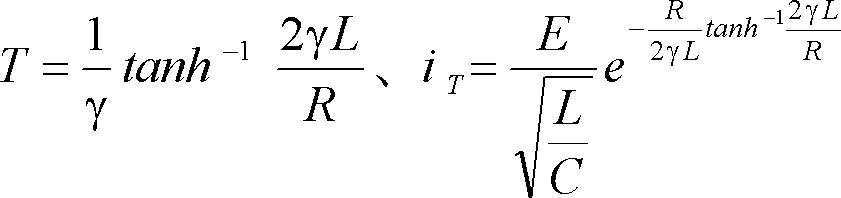
ケース3
