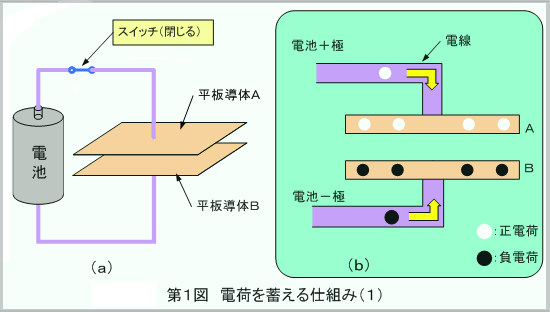
第1図(a)のように、スイッチを閉じて平行平板ABに電圧を加えると、同図(b)のように電池から平板導体へ電荷が流れ込みます。
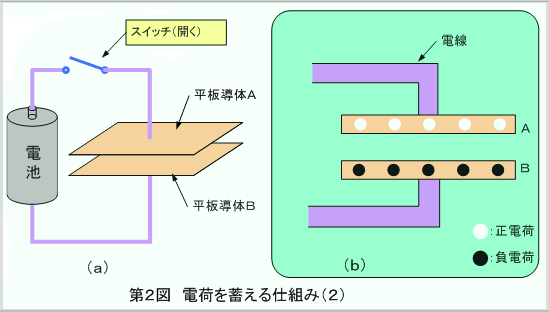
この状態で、第2図(a)のように、スイッチを開くと、平板AB上の電荷は異種であるため互いに吸引し合っているため電池には戻れず平板に取り残されます。同図(b)
このため、結果的に平板ABには異種同量の電荷が蓄えられたことになります。
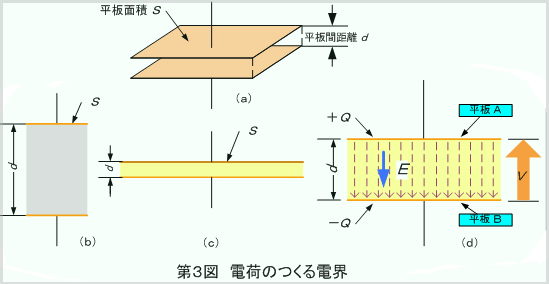
このとき、第3図(a)のように平板に挟まれた空間には電界ができ、同図(c)のように平板間距離に比べて平板の面積が非常に広い場合には、その電界は平等電界となります。
このときできる電界の大きさE[V/m]は、平板間に加えられた電圧がV[V]で、平板間距離がd[m]とすれば、
![]() ・・・・・(1)
・・・・・(1)
となります。
この電界は電池から入り込んだ電荷でつくられるわけですが、これを電気力線で考えると、ガウスの定理から「真空中では+Q[C]の電荷からは、Q/ε0[本]の電気力線が出る」ので、(d)図において、平板AからはQ/ε0[本]の電気力線が出、点線で示すように平板Bに入ります。電気力線はその密度が電界の大きさに等しくなるように定義されているので、平板の面積をS[m2]とすれば、
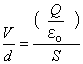 ・・・・・(2)
・・・・・(2)
の関係にあり、電池から入り込んだ電荷(平板上の電荷)Q は、
![]() ・・・・・(3)
・・・・・(3)
であることがわかります。
上例でとりあげた平行平板は「電荷を蓄える」働きをもっています。このように、「電荷を蓄える目的でつくられた装置」のことをコンデンサと呼んでいます。コンデンサにおいて電荷を実際に蓄えている場所(上例では平板A,B)を電極と云います。
(3)式からわかるように、蓄えた電荷は印加電圧に比例するので、コンデンサの性能は、単位印加電圧あたりの蓄電電気量で表すのがよく、
![]() ・・・・・(4)
・・・・・(4)
と定義します。ここで、C のことを静電容量と呼びます。
単位は、(4)式で示したように、F(ファラッド)を用います。
したがって、平行平板コンデンサの静電容量C は、(3)式から、
![]() ・・・・・(5)
・・・・・(5)
となります。
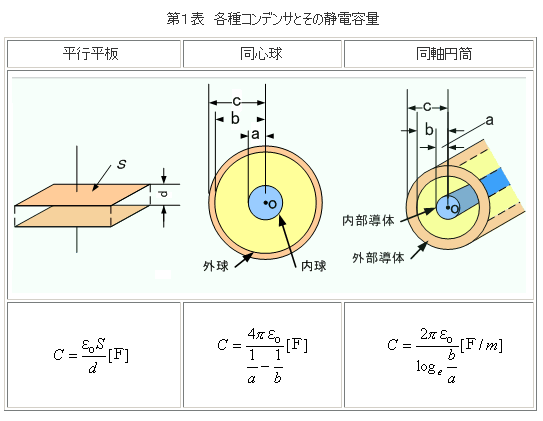
第1表にはいろいろな電極形状のコンデンサの例を示します。
第3図(d)の平行平板コンデンサで、電極AB間に絶縁物を入れて第1図の時と同じ電圧Vを印加してみると、AB間の電界は外部から強制的に第3図と同じV/d=Eとなります。このため、絶縁物はこの電界中にさらされたことになります。このときの絶縁物を第4図(a)とすると、
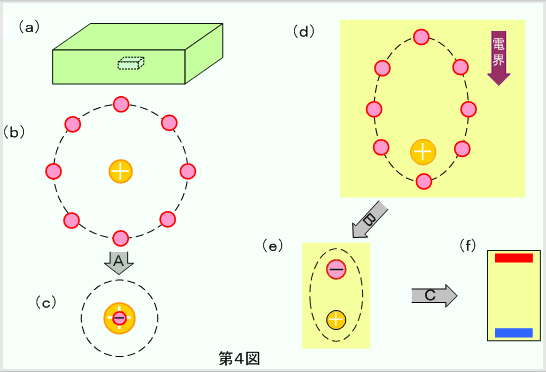
この絶縁物電界中にあるため電気分極(同図(d))が起こります。この結果、第5図のように電極ABともに、分極電荷によって電界が弱められるように作用しますが、電界は外部から強制的にV/dとされているため、この強さの電界を保つために新たに「分極電荷によって弱められた分」だけの電荷が電源部から追加補給されることになります。
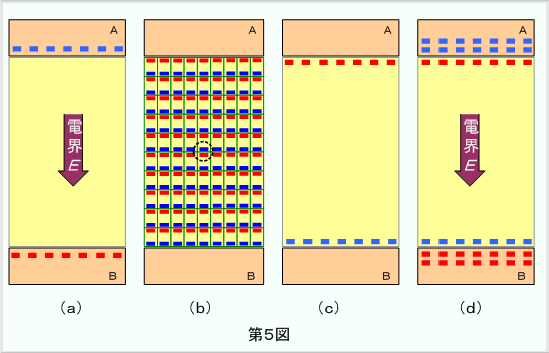
このため、同じ電圧を印加しても、絶縁物を入れた方が入れない場合に比べて電極の電荷が増加します。いま、電荷が元の電荷QのεS倍増加したとすると、
絶縁物を入れない場合の静電容量をC0とすれば、C0=Q/Vなので、絶縁物を入れたときの静電容量C
は、
![]() ・・・・・(6)
・・・・・(6)
となり、静電容量が絶縁物を入れない場合に比べεS倍になることを意味します。
この場合、キーとなるεSは比誘電率と呼ばれ、その物質固有の数値をもっています。第2表にはその概数を示します。
第2表 比誘電率の概数
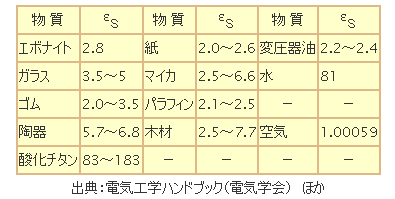
同表でわかるように、εSは1より大きい数値なので、一般に使用されるコンデンサはそのほとんどには絶縁物が入れられています。その種類XXをとって、XXコンデンサというように呼ばれています。
電気分極を起こす現象を誘電現象と呼んでいます。このため、誘電現象を起こす物質のことを誘電体と云います。したがって、絶縁物は誘電現象に注目した場合は誘電体といいます。先に述べた比誘電率は誘電体の誘電現象の強弱を表すデータということができます。
また、真空の誘電率ε0と比誘電率εSとの積は誘電体の誘電率といいます。(ε=ε0・εS)
したがって、絶縁物を入れたときの静電容量C は、
![]() ・・・・・(7)
・・・・・(7)
と表せ、(5)式でε0をεに置き換えることで扱える関係になっていることがわかります。


