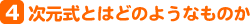計量単位の対象となる量として計るものには、実にいろいろな種類のものがある。例えば、長さ、質量、時間をはじめとして、面積、体積、速度、加速度、力、仕事、電気量、電圧、電流、抵抗、静電容量、インダクタンス、磁束、磁界の強さ、光度、照度、…… などいくらでもある。したがって、これらのものを測る単位にもそれだけ種類があるわけである。こうした単位の成り立ちや使い方について理解を深めていこう。


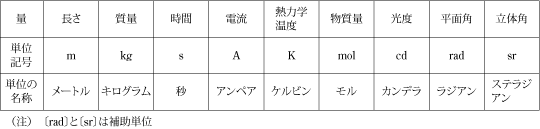
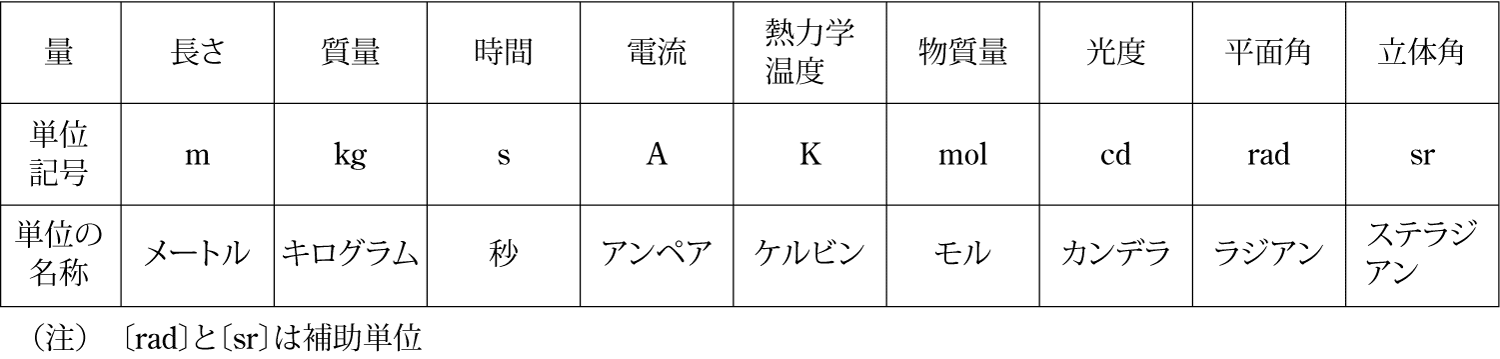
わが国においては、1960年以来、国際単位系(SI単位系)を標準として用いている。ここでは、7個の基本単位と2個の補助単位とそれらの単位を掛けたり、割ったりすることによって組み立てた多数の組立単位について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
※テキスト中の図はクリックすると大きく表示されます
一人、二人…という人数や一冊、二冊…という本の数のように、同一種類の物の数を表すのに用いられる単位を自然単位という。これに対して、ビルの高さ30m、上る時間5分などというときに使う同一種類の物理量を表すのに用いられる単位を計量単位という。計量単位は物理的に、ある基準となる量を決め、その基準量の何倍であるかを示すのに用いられる。
計量単位の対象となる量として計るものには、実にいろいろな種類のものがある。例えば、長さ、質量、時間をはじめとして、面積、体積、速度、加速度、力、仕事、電気量、電圧、電流、抵抗、静電容量、インダクタンス、磁束、磁界の強さ、光度、照度、…… などいくらでもある。したがって、これらのものを測る単位にもそれだけ種類があるわけである。こうした単位の成り立ちや使い方について理解を深めていこう。
SIは第1表に示すように、7個の基本単位と2個の補助単位とそれらの単位を掛けたり、割ったりすることによって組み立てた多数の組立単位で構成されている。SI単位系はMKS単位系の発展したものにすぎず、新しいものといえば、圧力や応力の単位〔N/m2〕を〔Pa〕にすること、コンダクタンスの単位〔Ω-1〕を〔S〕にすることなどである。 SI単位でなくても、〔min〕、〔h〕、 〔l〕、〔t〕、〔eV〕など重要なものは依然として使われている。また、温度の単位はSI基本単位では〔K〕であるが、実用的には従来どおりセルシウス温度の〔℃〕 を使ってよい。
*セルシウス温度というのは、水の凝固点を0℃と定め、水の沸点を100℃と定めて、0℃と100℃ の間を100等分した温度目盛である。セルシウス温度の0℃は熱力学温度(絶対温度)の273.15K 、100℃ は373.15K に相当する。熱力学温度Tとセルシウス温度tの関係はT=t+273.15 である。
第2表は基本単位の組み合わせと組立単位の関係を示したものである。
第2表で 1kg・m/s2 =1N である。つまり〔N〕という単位は、組立単位のうちの固有の名称をもつ単位の一つである。
更に、これを基に仕事について考えてみる。日常生活で仕事というときには商店の店員をしたり、自動車を運転したりすることをいうが、物理でいう仕事には必ず力が関係する。であるから、力の作用のないものは物理では仕事といわない。物理でいう仕事とは、ある物体に対して力を加えたとき、力の方向にその物体が動いたとき、その力(または物体)は仕事をしたという。そのときの仕事の大きさは(力の大きさ)と(動いた距離)との積で表す。
すなわち、仕事量=力×距離によって、
力の単位〔N〕×長さの単位〔m〕=仕事量の単位〔N・m〕
である。このほか一つの記号だけで表す〔J〕も仕事量の単位である。1J の仕事とは、1N の力で物体を1m だけその力の方向に物体を移動させたときに、力が物体にした仕事量である。このことから、
1J=1N×1m=1N・m
また、電気の場合には、1J は1W の電力が1s 間にする仕事である。
1J=1W×1s=1W・s
これを〔cal〕単位で表すと、1J =0.24cal の関係がある。
(例題1)
1マイクロメートル(μm=0.001mm)や1オングストローム((解答)
1μmや1(例題2)
同じ物理量は同じ単位で表される。では、同じ単位は同じ物理量を表しているといってよいか。(解答)
必ずしもそうではない。仕事量の単位は〔N・m〕であるし、ト ルクの単位も〔N・m〕である。〔N・m〕という単位を見ただけでは、それが仕事量を表すのか、トルクを表すのか分からない。いま、速さの単位を〔V〕、長さ、時間の単位をそれぞれ〔L〕、〔T〕の記号で示すことにすると、V、L、Tの間には次の関係がある。
V = L/T =L1T-1
このような関係式を次元式という。
例えば、長さの単位をL とすれば、面積A の次元式はA =L2、体積Vの次元式はV =L3となる。
(例題3)
次のものの次元式を求めよ(1) 加速度 (2) 密度 (3) 力
(解答)
(1) 加速度は単位時間に速度が変化する割合である。〔m/s〕という単位で表せる速度が、1秒間に変化する割合を単位とするのが加速度の単位となる。したがって、加速度の単位は〔m/s2〕となるから長さ、時間の単位をL、Tという記号で表すと、加速度の次元式は、
L / T2=LT-2
となる。
(2) 密度は、単位体積当たりの質量の大きさで示される。
質量、長さ、体積の単位記号をM、L、Vで表すと、密度ρの次元式は、
ρ=M/V=M/L3=ML-3
となる。
(3) 力の単位の組み立てを考えると、力が質量をもったものに働けば、静止している状態を動かしたり、動いているものを静止させたり、その速さを変えたりする。つまり、物体に加速度を生じさせる働きをもっている。そしてこの力の大きさFは質量mと加速度αの積で表される。すなわち、
F=mα
となる。
質量の単位に〔kg〕、加速度の単位に〔m/s2〕を使うと、このときの 力の単位は〔kg・m/s2〕という構成になる。この力の単位が〔N〕であるが、その次元式は、
ML/T2=MLT-2
となり、〔質量×長さ×時間-2〕の形となる。
(例題4)
質量と重量はどのように違うか(解答)
地球上では、物体にはその質量に比例した重力が働くが、これも力である。この力を重量というが、重量によって我々は質量の大きさを感じとっている。質量1kg の物体に標準の重力加速度g( = 9.80665 m / s2)が働いたときの力が重量であり、重量とはおおざっぱにいえば、1kg の物体を持ち上げているときの力である。すなわち、質量1kg の物体の重量は9.8N である。〜終わり〜
■ぜひアンケートにご協力下さい■