ところが、実はこの別世界の感じのする


交流回路は、ベクトルを用いて計算することができる。ベクトルは図形を基本としたものであるが、図形に頼るだけでは複雑な回路になると限界が生じてくる。そこでベクトルによる図形処理を数式計算に置き換えることができれば計算が容易になる。ここでは、ベクトルの複素数表現と、それを用いたベクトル合成の計算方法を解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
※テキスト中の図はクリックすると大きく表示されます
いま方程式
ところが、実はこの別世界の感じのする
この
根号の中が負になる数はみな虚数であるが、特に
例えば、
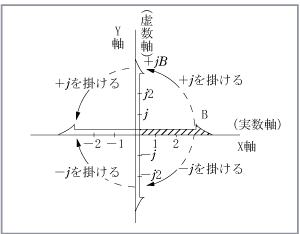
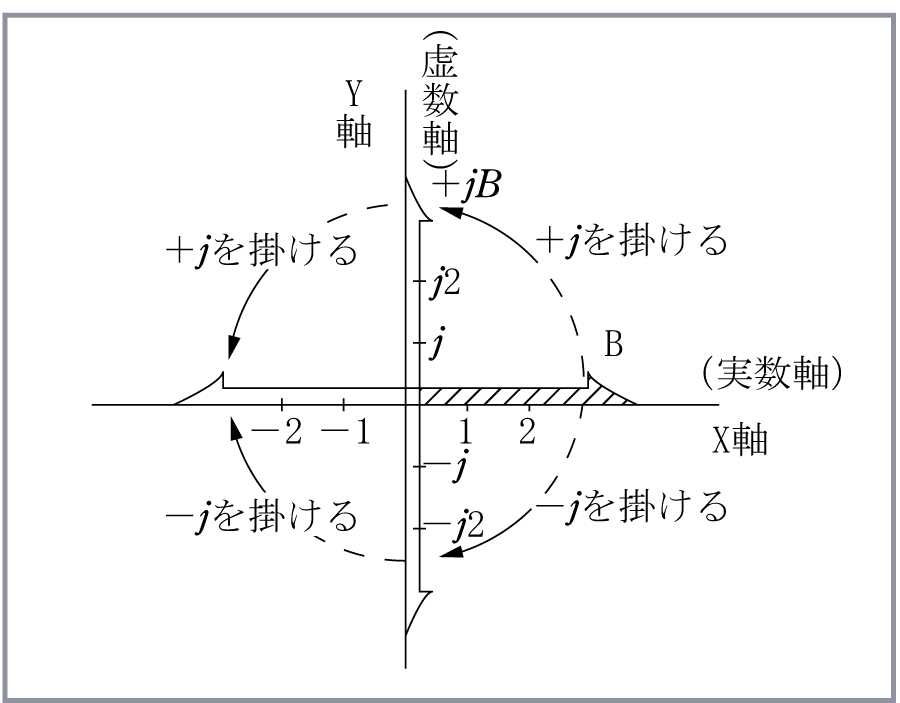
このような性質を、電気の計算にうまく利用しようというのが、虚数を使う大きなねらいなのである。希望はベクトル図を
みなさんは、座標といえば、中学校以来なじみの深い、X 軸 とY軸をもった座標を思い浮かべるかもしれない。ところが、この座標上の点は、みんな実数の点しかおくことができないため
この
発電機はコイルが回転して交流を生み出すが、交流を数学的に処理するのに虚数
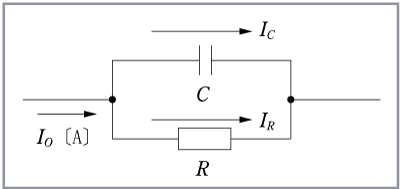
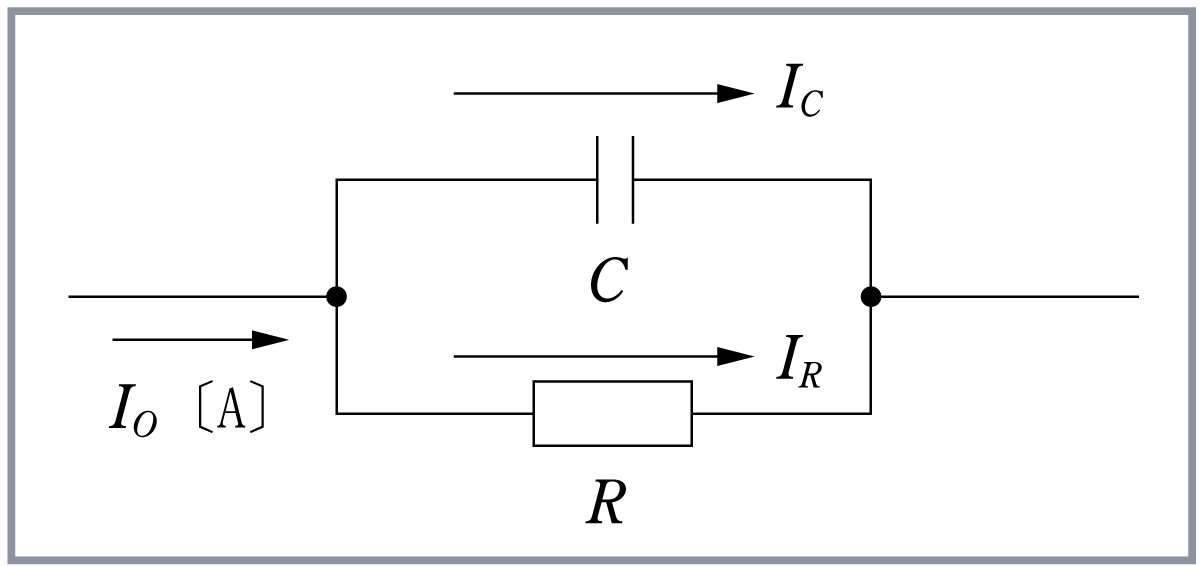
普通に考えて、抵抗を流れる電流
したがって、
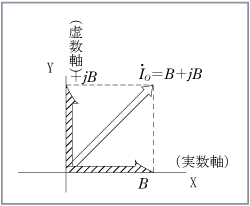
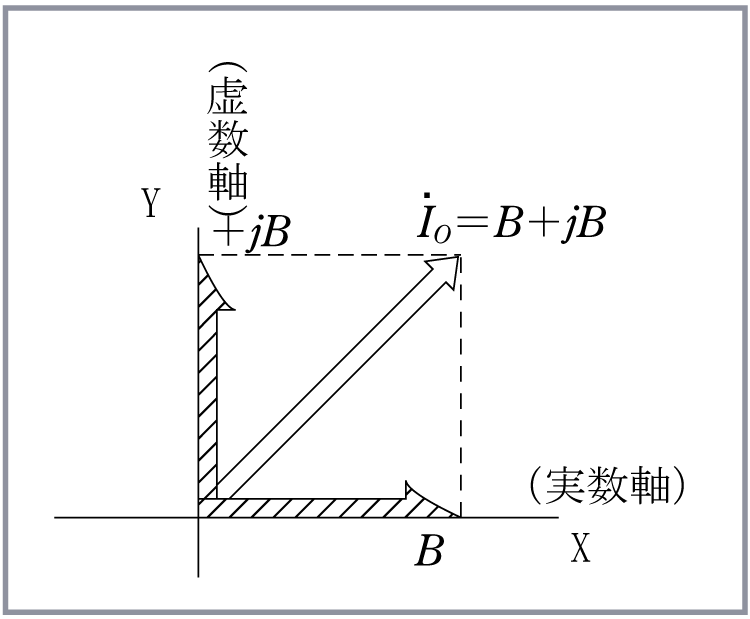
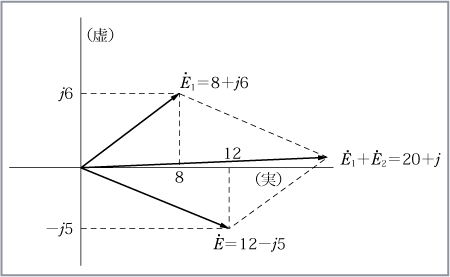
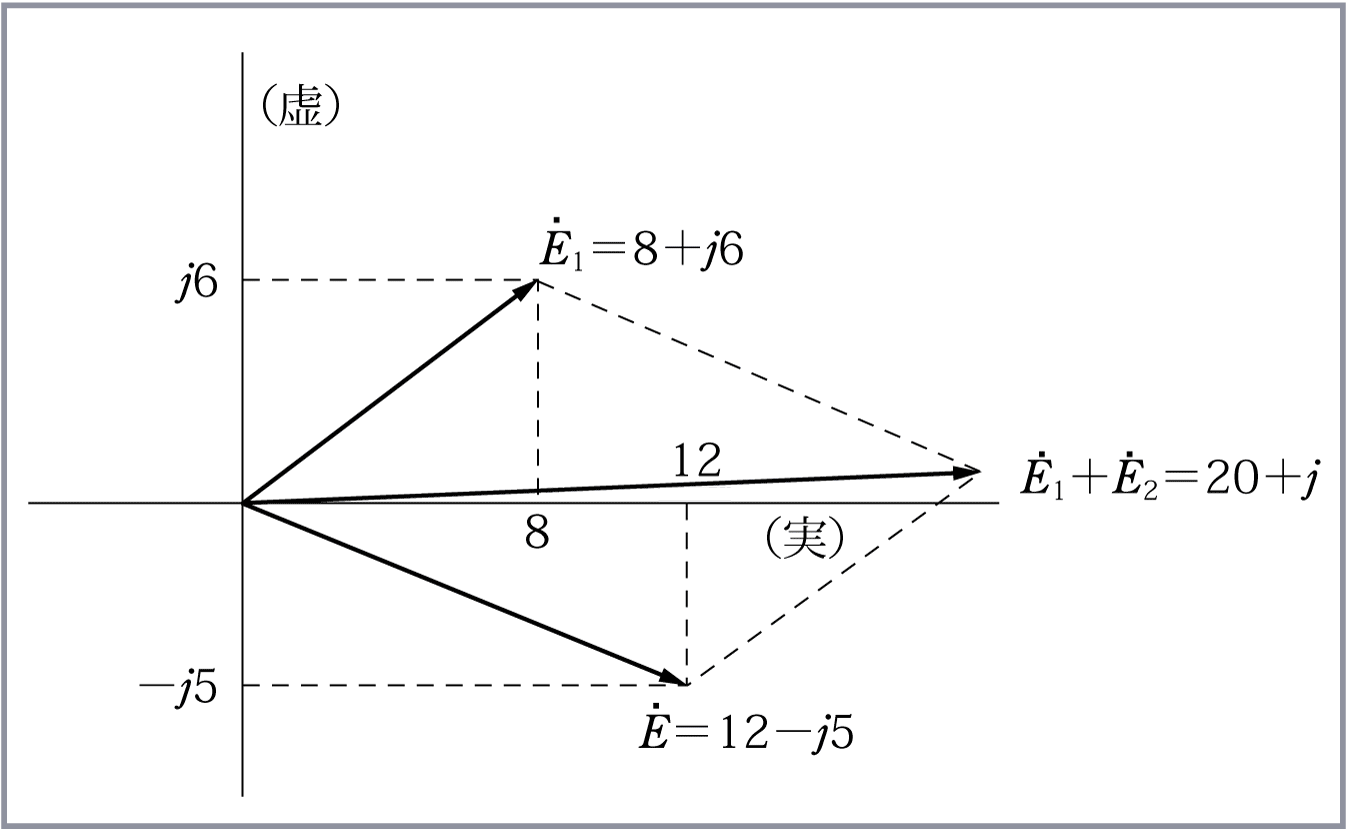
これは算術和だからベクトル和でなければだめではないか、と思う人がいるかもしれない。 ところがどうだろう、複素平面上におかれた
さて
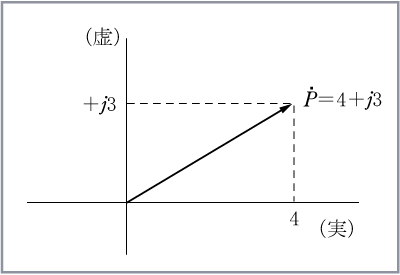
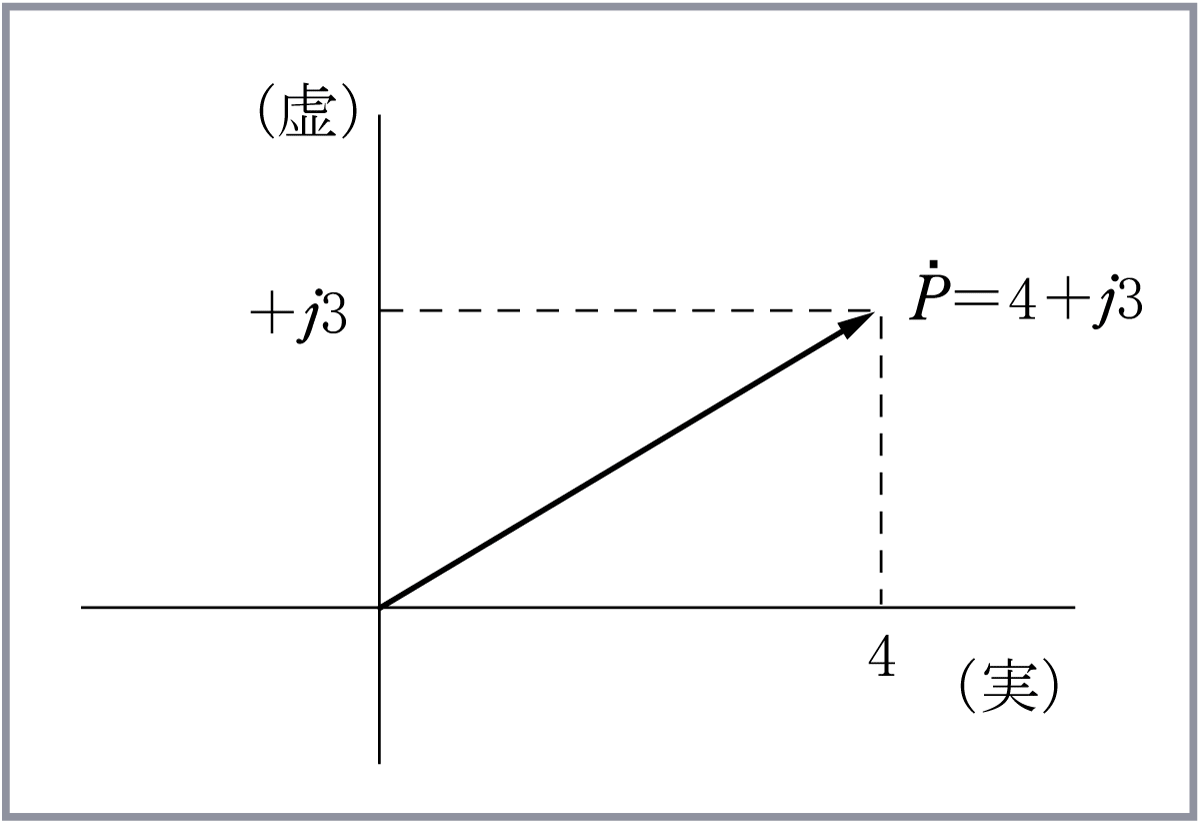
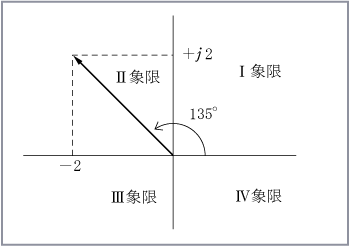
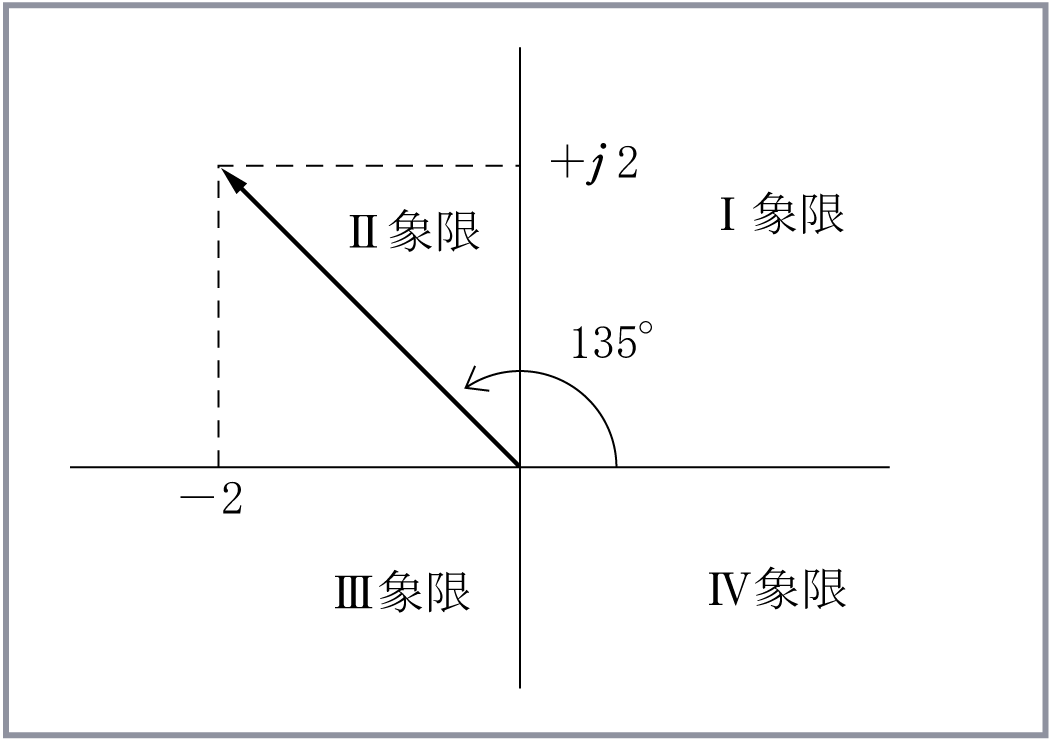
〔例題〕 次の複素数で表される電圧のベクトル図を描き、
〔解答〕 電圧の複素数表示をベクトルで示すと第6図のようになる。
〜終わり〜
■ぜひアンケートにご協力下さい■