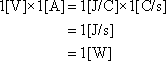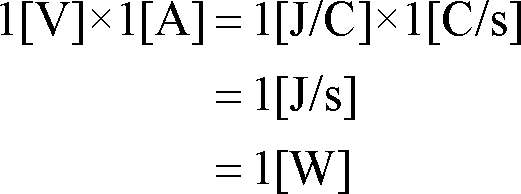電力に関する重要公式 電力[W] =電圧[V]×電流[A]は、電気理論の学習者には大変なじみ深いものである。電圧[V]と電流[A]はいずれも電気系の単位であるが、電力[W]は力学系の単位なので一見矛盾がある。ここでは、電圧の単位[V]、電流の単位[A]がいずれも電気による力学現象に基づき決められた力学単位を基礎にして定義された単位であることを解説し、電気系、力学系のエネルギーとその単位時間当たりの授受について理解を深める。
Update Required To play the media you will need to either update your browser to a recent version or update your
Flash plugin.
※テキスト中の図はクリックすると大きく表示されます

電力に関する重要公式 電圧[V]×電流[A]=電力[W] は、電気理論の学習者には大変なじみ深いものである。
ところで、電圧[V]と電流[A]はいずれも電気系の単位であるが、電力の単位[W]は力学系の単位である。
つまり[W]は、
となるから力学系の単位である。そこで、電気系の単位と力学系の単位のものを等しいと置いているこの式は正しいのだろうかという疑問が生じる。果たしてこの式には矛盾がないのだろうか。
実は、この着眼点は一理あるように思えるが、大きな誤りがある。電圧の単位[V]も電流の単位[A]も、いずれも電気による力学現象に基づいて決められた力学単位が基礎になっているのである。
![02.電圧[V]と電流[A]の単位の成り立ち](image/topic/02.gif)
いま、電界中の2点、A点からB点に向かって1[C]の電荷を移動させた場合、この電荷はクーロンの法則に基づく力の作用を受けるから、この電荷を移動させるにはクーロン力に打ち勝つだけの力を与える必要がある。つまり、力学的な仕事が必要になる。結局A点からB点まで電荷を運ぶためにはエネルギーを必要とする。このエネルギー[J]の大きさを、AB2点間の電位差または電圧と定義し、単位[V]と定めている(第1図)。
これを式で表せば次のようになる。
次に電荷と電流の関係を考えてみよう。
電荷の移動を電流と呼び、ある断面を1秒間に1[C]通過したもの1[A]と定義している。すなわち、電荷=電流×時間であるから、その単位の関係を式で表すと、
![03.[V]×[A]=[W]の成り立つ理由](image/topic/03.gif)
ここで、(2)式と(3)式を右辺同士、左辺同士掛け合わせてみると、
すなわち、[V]×[A]=[W]が成り立つ。
上式の整理の過程でクーロン[C]という単位は結果として消去されているが、1[C]という値は勝手に定められたものではなく、クーロン力を基にその大きさが決められている。AB2点間に電荷Q[C]が置かれている場合、この電荷間に働くクーロン力F[N]は次式で示される。(第2図)
ここで

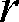
=1[m]としたとき、AB2点間に
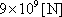
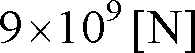
の力が作用した場合、電荷
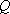
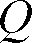
は1[C]の電気量をもつと約束されているのである。このように1[C]という電荷(電気量)の単位は、[m]とか[N]とか、力学系で使われる単位に関連づけられている。
[V]×[A]=[W]の説明過程で、陰にクーロンという力学系に関係する単位が隠れていることに気付いてほしい。